Rectangular function with a = 1 The rectangular function (also known as the rectangle function , rect function , Pi function , Heaviside Pi function ,[ 1] gate function , unit pulse , or the normalized boxcar function ) is defined as[ 2]
rect
(
t
a
)
=
Π
(
t
a
)
=
{
0
,
if
|
t
|
>
a
2
1
2
,
if
|
t
|
=
a
2
1
,
if
|
t
|
<
a
2
.
{\displaystyle \operatorname {rect} \left({\frac {t}{a}}\right)=\Pi \left({\frac {t}{a}}\right)=\left\{{\begin{array}{rl}0,&{\text{if }}|t|>{\frac {a}{2}}\\{\frac {1}{2}},&{\text{if }}|t|={\frac {a}{2}}\\1,&{\text{if }}|t|<{\frac {a}{2}}.\end{array}}\right.}
Alternative definitions of the function define
rect
(
±
1
2
)
{\textstyle \operatorname {rect} \left(\pm {\frac {1}{2}}\right)}
[ 3] [ 4] [ 5]
Its periodic version is called a rectangular wave
History
The rect function has been introduced 1953 by Woodward [ 6] [ 7] cutout operator , together with the sinc function[ 8] [ 9] interpolation operator , and their counter operations which are sampling (comb operatorreplicating (rep operator
Relation to the boxcar function
The rectangular function is a special case of the more general boxcar function :
rect
(
t
−
X
Y
)
=
H
(
t
−
(
X
−
Y
/
2
)
)
−
H
(
t
−
(
X
+
Y
/
2
)
)
=
H
(
t
−
X
+
Y
/
2
)
−
H
(
t
−
X
−
Y
/
2
)
{\displaystyle \operatorname {rect} \left({\frac {t-X}{Y}}\right)=H(t-(X-Y/2))-H(t-(X+Y/2))=H(t-X+Y/2)-H(t-X-Y/2)}
where
H
(
x
)
{\displaystyle H(x)}
Heaviside step function ; the function is centered at
X
{\displaystyle X}
Y
{\displaystyle Y}
X
−
Y
/
2
{\displaystyle X-Y/2}
X
+
Y
/
2.
{\displaystyle X+Y/2.}
Plot of normalized
sinc
(
x
)
{\displaystyle \operatorname {sinc} (x)}
sinc
(
π
x
)
{\displaystyle \operatorname {sinc} (\pi x)}
The unitary Fourier transforms of the rectangular function are[ 2]
∫
−
∞
∞
rect
(
t
)
⋅
e
−
i
2
π
f
t
d
t
=
sin
(
π
f
)
π
f
=
sinc
(
π
f
)
=
sinc
π
(
f
)
,
{\displaystyle \int _{-\infty }^{\infty }\operatorname {rect} (t)\cdot e^{-i2\pi ft}\,dt={\frac {\sin(\pi f)}{\pi f}}=\operatorname {sinc} (\pi f)=\operatorname {sinc} _{\pi }(f),}
f , where
sinc
π
{\displaystyle \operatorname {sinc} _{\pi }}
[ 10] sinc function and
1
2
π
∫
−
∞
∞
rect
(
t
)
⋅
e
−
i
ω
t
d
t
=
1
2
π
⋅
sin
(
ω
/
2
)
ω
/
2
=
1
2
π
⋅
sinc
(
ω
/
2
)
,
{\displaystyle {\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\operatorname {rect} (t)\cdot e^{-i\omega t}\,dt={\frac {1}{\sqrt {2\pi }}}\cdot {\frac {\sin \left(\omega /2\right)}{\omega /2}}={\frac {1}{\sqrt {2\pi }}}\cdot \operatorname {sinc} \left(\omega /2\right),}
ω
{\displaystyle \omega }
sinc
{\displaystyle \operatorname {sinc} }
sinc function .
For
rect
(
x
/
a
)
{\displaystyle \operatorname {rect} (x/a)}
∫
−
∞
∞
rect
(
t
a
)
⋅
e
−
i
2
π
f
t
d
t
=
a
sin
(
π
a
f
)
π
a
f
=
a
sinc
π
(
a
f
)
.
{\displaystyle \int _{-\infty }^{\infty }\operatorname {rect} \left({\frac {t}{a}}\right)\cdot e^{-i2\pi ft}\,dt=a{\frac {\sin(\pi af)}{\pi af}}=a\ \operatorname {sinc} _{\pi }{(af)}.}
Relation to the triangular function
We can define the triangular function as the convolution of two rectangular functions:
t
r
i
(
t
/
T
)
=
r
e
c
t
(
2
t
/
T
)
∗
r
e
c
t
(
2
t
/
T
)
.
{\displaystyle \operatorname {tri(t/T)} =\operatorname {rect(2t/T)} *\operatorname {rect(2t/T)} .\,}
Use in probability
Viewing the rectangular function as a probability density function , it is a special case of the continuous uniform distribution with
a
=
−
1
/
2
,
b
=
1
/
2.
{\displaystyle a=-1/2,b=1/2.}
characteristic function is
φ
(
k
)
=
sin
(
k
/
2
)
k
/
2
,
{\displaystyle \varphi (k)={\frac {\sin(k/2)}{k/2}},}
and its moment-generating function is
M
(
k
)
=
sinh
(
k
/
2
)
k
/
2
,
{\displaystyle M(k)={\frac {\sinh(k/2)}{k/2}},}
where
sinh
(
t
)
{\displaystyle \sinh(t)}
hyperbolic sine function.
Rational approximation
The pulse function may also be expressed as a limit of a rational function :
Π
(
t
)
=
lim
n
→
∞
,
n
∈
(
Z
)
1
(
2
t
)
2
n
+
1
.
{\displaystyle \Pi (t)=\lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{(2t)^{2n}+1}}.}
Demonstration of validity
First, we consider the case where
|
t
|
<
1
2
.
{\textstyle |t|<{\frac {1}{2}}.}
(
2
t
)
2
n
{\textstyle (2t)^{2n}}
n
.
{\displaystyle n.}
2
t
<
1
{\displaystyle 2t<1}
(
2
t
)
2
n
{\textstyle (2t)^{2n}}
n
.
{\displaystyle n.}
It follows that:
lim
n
→
∞
,
n
∈
(
Z
)
1
(
2
t
)
2
n
+
1
=
1
0
+
1
=
1
,
|
t
|
<
1
2
.
{\displaystyle \lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{(2t)^{2n}+1}}={\frac {1}{0+1}}=1,|t|<{\tfrac {1}{2}}.}
Second, we consider the case where
|
t
|
>
1
2
.
{\textstyle |t|>{\frac {1}{2}}.}
(
2
t
)
2
n
{\textstyle (2t)^{2n}}
n
.
{\displaystyle n.}
2
t
>
1
{\displaystyle 2t>1}
(
2
t
)
2
n
{\textstyle (2t)^{2n}}
n
.
{\displaystyle n.}
It follows that:
lim
n
→
∞
,
n
∈
(
Z
)
1
(
2
t
)
2
n
+
1
=
1
+
∞
+
1
=
0
,
|
t
|
>
1
2
.
{\displaystyle \lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{(2t)^{2n}+1}}={\frac {1}{+\infty +1}}=0,|t|>{\tfrac {1}{2}}.}
Third, we consider the case where
|
t
|
=
1
2
.
{\textstyle |t|={\frac {1}{2}}.}
lim
n
→
∞
,
n
∈
(
Z
)
1
(
2
t
)
2
n
+
1
=
lim
n
→
∞
,
n
∈
(
Z
)
1
1
2
n
+
1
=
1
1
+
1
=
1
2
.
{\displaystyle \lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{(2t)^{2n}+1}}=\lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{1^{2n}+1}}={\frac {1}{1+1}}={\tfrac {1}{2}}.}
We see that it satisfies the definition of the pulse function. Therefore,
rect
(
t
)
=
Π
(
t
)
=
lim
n
→
∞
,
n
∈
(
Z
)
1
(
2
t
)
2
n
+
1
=
{
0
if
|
t
|
>
1
2
1
2
if
|
t
|
=
1
2
1
if
|
t
|
<
1
2
.
{\displaystyle \operatorname {rect} (t)=\Pi (t)=\lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{(2t)^{2n}+1}}={\begin{cases}0&{\mbox{if }}|t|>{\frac {1}{2}}\\{\frac {1}{2}}&{\mbox{if }}|t|={\frac {1}{2}}\\1&{\mbox{if }}|t|<{\frac {1}{2}}.\\\end{cases}}}
Dirac delta function
The rectangle function can be used to represent the Dirac delta function
δ
(
x
)
{\displaystyle \delta (x)}
[ 11]
δ
(
x
)
=
lim
a
→
0
1
a
rect
(
x
a
)
.
{\displaystyle \delta (x)=\lim _{a\to 0}{\frac {1}{a}}\operatorname {rect} \left({\frac {x}{a}}\right).}
g
(
x
)
{\displaystyle g(x)}
a
{\displaystyle a}
g
a
v
g
(
0
)
=
1
a
∫
−
∞
∞
d
x
g
(
x
)
rect
(
x
a
)
.
{\displaystyle g_{avg}(0)={\frac {1}{a}}\int \limits _{-\infty }^{\infty }dx\ g(x)\operatorname {rect} \left({\frac {x}{a}}\right).}
g
(
0
)
{\displaystyle g(0)}
g
(
0
)
=
lim
a
→
0
1
a
∫
−
∞
∞
d
x
g
(
x
)
rect
(
x
a
)
{\displaystyle g(0)=\lim _{a\to 0}{\frac {1}{a}}\int \limits _{-\infty }^{\infty }dx\ g(x)\operatorname {rect} \left({\frac {x}{a}}\right)}
g
(
0
)
=
∫
−
∞
∞
d
x
g
(
x
)
δ
(
x
)
.
{\displaystyle g(0)=\int \limits _{-\infty }^{\infty }dx\ g(x)\delta (x).}
δ
(
t
)
{\displaystyle \delta (t)}
δ
(
f
)
=
∫
−
∞
∞
δ
(
t
)
⋅
e
−
i
2
π
f
t
d
t
=
lim
a
→
0
1
a
∫
−
∞
∞
rect
(
t
a
)
⋅
e
−
i
2
π
f
t
d
t
=
lim
a
→
0
sinc
(
a
f
)
.
{\displaystyle \delta (f)=\int _{-\infty }^{\infty }\delta (t)\cdot e^{-i2\pi ft}\,dt=\lim _{a\to 0}{\frac {1}{a}}\int _{-\infty }^{\infty }\operatorname {rect} \left({\frac {t}{a}}\right)\cdot e^{-i2\pi ft}\,dt=\lim _{a\to 0}\operatorname {sinc} {(af)}.}
sinc function here is the normalized sinc function. Because the first zero of the sinc function is at
f
=
1
/
a
{\displaystyle f=1/a}
a
{\displaystyle a}
δ
(
t
)
{\displaystyle \delta (t)}
δ
(
f
)
=
1
,
{\displaystyle \delta (f)=1,}
See also
References
^ Wolfram Research (2008). "HeavisidePi, Wolfram Language function" . Retrieved October 11, 2022 . ^ a b Weisstein, Eric W. "Rectangle Function" . MathWorld ^ Wang, Ruye (2012). Introduction to Orthogonal Transforms: With Applications in Data Processing and Analysis 135– 136. ISBN 9780521516884 . ^ Tang, K. T. (2007). Mathematical Methods for Engineers and Scientists: Fourier analysis, partial differential equations and variational models ISBN 9783540446958 . ^ Kumar, A. Anand (2011). Signals and Systems 258– 260. ISBN 9788120343108 . ^ Klauder, John R (1960). "The Theory and Design of Chirp Radars" Bell System Technical Journal . 39 (4): 745– 808. doi :10.1002/j.1538-7305.1960.tb03942.x . ^ Woodward, Philipp M (1953). Probability and Information Theory, with Applications to Radar . Pergamon Press. p. 29. ^ Higgins, John Rowland (1996). Sampling Theory in Fourier and Signal Analysis: Foundations . Oxford University Press Inc. p. 4. ISBN 0198596995 . ^ Zayed, Ahmed I (1996). Handbook of Function and Generalized Function Transformations . CRC Press. p. 507. ISBN 9780849380761 . ^ Wolfram MathWorld, https://mathworld.wolfram.com/SincFunction.html
^ Khare, Kedar; Butola, Mansi; Rajora, Sunaina (2023). "Chapter 2.4 Sampling by Averaging, Distributions and Delta Function". Fourier Optics and Computational Imaging (2nd ed.). Springer. pp. 15– 16. doi :10.1007/978-3-031-18353-9 . ISBN 978-3-031-18353-9 . 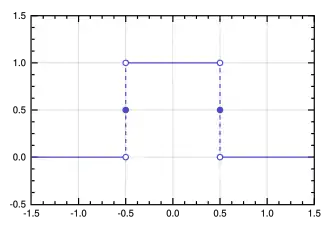
.svg.png)