In trigonometry , trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involving certain functions of one or more angles . They are distinct from triangle identities , which are identities potentially involving angles but also involving side lengths or other lengths of a triangle .
These identities are useful whenever expressions involving trigonometric functions need to be simplified. An important application is the integration of non-trigonometric functions: a common technique involves first using the substitution rule with a trigonometric function , and then simplifying the resulting integral with a trigonometric identity.
Pythagorean identities
Trigonometric functions and their reciprocals on the unit circle. All of the right-angled triangles are similar, i.e. the ratios between their corresponding sides are the same. For sin, cos and tan the unit-length radius forms the hypotenuse of the triangle that defines them. The reciprocal identities arise as ratios of sides in the triangles where this unit line is no longer the hypotenuse. The triangle shaded blue illustrates the identity
1
+
cot
2
θ
=
csc
2
θ
{\displaystyle 1+\cot ^{2}\theta =\csc ^{2}\theta }
tan
2
θ
+
1
=
sec
2
θ
{\displaystyle \tan ^{2}\theta +1=\sec ^{2}\theta }
The basic relationship between the sine and cosine is given by the Pythagorean identity:
sin
2
θ
+
cos
2
θ
=
1
,
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1,}
where
sin
2
θ
{\displaystyle \sin ^{2}\theta }
(
sin
θ
)
2
{\displaystyle {(\sin \theta )}^{2}}
cos
2
θ
{\displaystyle \cos ^{2}\theta }
(
cos
θ
)
2
.
{\displaystyle {(\cos \theta )}^{2}.}
This can be viewed as a version of the Pythagorean theorem , and follows from the equation
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1}
unit circle . This equation can be solved for either the sine or the cosine:
sin
θ
=
±
1
−
cos
2
θ
,
cos
θ
=
±
1
−
sin
2
θ
.
{\displaystyle {\begin{aligned}\sin \theta &=\pm {\sqrt {1-\cos ^{2}\theta }},\\\cos \theta &=\pm {\sqrt {1-\sin ^{2}\theta }}.\end{aligned}}}
where the sign depends on the quadrant of
θ
.
{\displaystyle \theta .}
Dividing this identity by
sin
2
θ
{\displaystyle \sin ^{2}\theta }
cos
2
θ
{\displaystyle \cos ^{2}\theta }
1
+
cot
2
θ
=
csc
2
θ
1
+
tan
2
θ
=
sec
2
θ
sec
2
θ
+
csc
2
θ
=
sec
2
θ
csc
2
θ
{\displaystyle {\begin{aligned}&1+\cot ^{2}\theta =\csc ^{2}\theta \\&1+\tan ^{2}\theta =\sec ^{2}\theta \\&\sec ^{2}\theta +\csc ^{2}\theta =\sec ^{2}\theta \csc ^{2}\theta \end{aligned}}}
Using these identities, it is possible to express any trigonometric function in terms of any other (up to a plus or minus sign):
Each trigonometric function in terms of each of the other five.[ 1]
in terms of
sin
θ
{\displaystyle \sin \theta }
csc
θ
{\displaystyle \csc \theta }
cos
θ
{\displaystyle \cos \theta }
sec
θ
{\displaystyle \sec \theta }
tan
θ
{\displaystyle \tan \theta }
cot
θ
{\displaystyle \cot \theta }
sin
θ
=
{\displaystyle \sin \theta =}
sin
θ
{\displaystyle \sin \theta }
1
csc
θ
{\displaystyle {\frac {1}{\csc \theta }}}
±
1
−
cos
2
θ
{\displaystyle \pm {\sqrt {1-\cos ^{2}\theta }}}
±
sec
2
θ
−
1
sec
θ
{\displaystyle \pm {\frac {\sqrt {\sec ^{2}\theta -1}}{\sec \theta }}}
±
tan
θ
1
+
tan
2
θ
{\displaystyle \pm {\frac {\tan \theta }{\sqrt {1+\tan ^{2}\theta }}}}
±
1
1
+
cot
2
θ
{\displaystyle \pm {\frac {1}{\sqrt {1+\cot ^{2}\theta }}}}
csc
θ
=
{\displaystyle \csc \theta =}
1
sin
θ
{\displaystyle {\frac {1}{\sin \theta }}}
csc
θ
{\displaystyle \csc \theta }
±
1
1
−
cos
2
θ
{\displaystyle \pm {\frac {1}{\sqrt {1-\cos ^{2}\theta }}}}
±
sec
θ
sec
2
θ
−
1
{\displaystyle \pm {\frac {\sec \theta }{\sqrt {\sec ^{2}\theta -1}}}}
±
1
+
tan
2
θ
tan
θ
{\displaystyle \pm {\frac {\sqrt {1+\tan ^{2}\theta }}{\tan \theta }}}
±
1
+
cot
2
θ
{\displaystyle \pm {\sqrt {1+\cot ^{2}\theta }}}
cos
θ
=
{\displaystyle \cos \theta =}
±
1
−
sin
2
θ
{\displaystyle \pm {\sqrt {1-\sin ^{2}\theta }}}
±
csc
2
θ
−
1
csc
θ
{\displaystyle \pm {\frac {\sqrt {\csc ^{2}\theta -1}}{\csc \theta }}}
cos
θ
{\displaystyle \cos \theta }
1
sec
θ
{\displaystyle {\frac {1}{\sec \theta }}}
±
1
1
+
tan
2
θ
{\displaystyle \pm {\frac {1}{\sqrt {1+\tan ^{2}\theta }}}}
±
cot
θ
1
+
cot
2
θ
{\displaystyle \pm {\frac {\cot \theta }{\sqrt {1+\cot ^{2}\theta }}}}
sec
θ
=
{\displaystyle \sec \theta =}
±
1
1
−
sin
2
θ
{\displaystyle \pm {\frac {1}{\sqrt {1-\sin ^{2}\theta }}}}
±
csc
θ
csc
2
θ
−
1
{\displaystyle \pm {\frac {\csc \theta }{\sqrt {\csc ^{2}\theta -1}}}}
1
cos
θ
{\displaystyle {\frac {1}{\cos \theta }}}
sec
θ
{\displaystyle \sec \theta }
±
1
+
tan
2
θ
{\displaystyle \pm {\sqrt {1+\tan ^{2}\theta }}}
±
1
+
cot
2
θ
cot
θ
{\displaystyle \pm {\frac {\sqrt {1+\cot ^{2}\theta }}{\cot \theta }}}
tan
θ
=
{\displaystyle \tan \theta =}
±
sin
θ
1
−
sin
2
θ
{\displaystyle \pm {\frac {\sin \theta }{\sqrt {1-\sin ^{2}\theta }}}}
±
1
csc
2
θ
−
1
{\displaystyle \pm {\frac {1}{\sqrt {\csc ^{2}\theta -1}}}}
±
1
−
cos
2
θ
cos
θ
{\displaystyle \pm {\frac {\sqrt {1-\cos ^{2}\theta }}{\cos \theta }}}
±
sec
2
θ
−
1
{\displaystyle \pm {\sqrt {\sec ^{2}\theta -1}}}
tan
θ
{\displaystyle \tan \theta }
1
cot
θ
{\displaystyle {\frac {1}{\cot \theta }}}
cot
θ
=
{\displaystyle \cot \theta =}
±
1
−
sin
2
θ
sin
θ
{\displaystyle \pm {\frac {\sqrt {1-\sin ^{2}\theta }}{\sin \theta }}}
±
csc
2
θ
−
1
{\displaystyle \pm {\sqrt {\csc ^{2}\theta -1}}}
±
cos
θ
1
−
cos
2
θ
{\displaystyle \pm {\frac {\cos \theta }{\sqrt {1-\cos ^{2}\theta }}}}
±
1
sec
2
θ
−
1
{\displaystyle \pm {\frac {1}{\sqrt {\sec ^{2}\theta -1}}}}
1
tan
θ
{\displaystyle {\frac {1}{\tan \theta }}}
cot
θ
{\displaystyle \cot \theta }
By examining the unit circle, one can establish the following properties of the trigonometric functions.
Reflections
Transformation of coordinates (a ,b ) when shifting the reflection angle
α
{\displaystyle \alpha }
π
4
{\displaystyle {\frac {\pi }{4}}}
When the direction of a Euclidean vector is represented by an angle
θ
,
{\displaystyle \theta ,}
x
{\displaystyle x}
Euclidean space , where the angle is that determined by a parallel to the given line through the origin and the positive
x
{\displaystyle x}
θ
{\displaystyle \theta }
α
,
{\displaystyle \alpha ,}
θ
′
{\displaystyle \theta ^{\prime }}
θ
′
=
2
α
−
θ
.
{\displaystyle \theta ^{\prime }=2\alpha -\theta .}
The values of the trigonometric functions of these angles
θ
,
θ
′
{\displaystyle \theta ,\;\theta ^{\prime }}
α
{\displaystyle \alpha }
reduction formulae .[ 2]
θ
{\displaystyle \theta }
α
=
0
{\displaystyle \alpha =0}
[ 3] odd/even identities
θ
{\displaystyle \theta }
α
=
π
4
{\displaystyle \alpha ={\frac {\pi }{4}}}
θ
{\displaystyle \theta }
α
=
π
2
{\displaystyle \alpha ={\frac {\pi }{2}}}
θ
{\displaystyle \theta }
α
=
3
π
4
{\displaystyle \alpha ={\frac {3\pi }{4}}}
θ
{\displaystyle \theta }
α
=
π
{\displaystyle \alpha =\pi }
compare to
α
=
0
{\displaystyle \alpha =0}
sin
(
−
θ
)
=
−
sin
θ
{\displaystyle \sin(-\theta )=-\sin \theta }
sin
(
π
2
−
θ
)
=
cos
θ
{\displaystyle \sin \left({\tfrac {\pi }{2}}-\theta \right)=\cos \theta }
sin
(
π
−
θ
)
=
+
sin
θ
{\displaystyle \sin(\pi -\theta )=+\sin \theta }
sin
(
3
π
2
−
θ
)
=
−
cos
θ
{\displaystyle \sin \left({\tfrac {3\pi }{2}}-\theta \right)=-\cos \theta }
sin
(
2
π
−
θ
)
=
−
sin
(
θ
)
=
sin
(
−
θ
)
{\displaystyle \sin(2\pi -\theta )=-\sin(\theta )=\sin(-\theta )}
cos
(
−
θ
)
=
+
cos
θ
{\displaystyle \cos(-\theta )=+\cos \theta }
cos
(
π
2
−
θ
)
=
sin
θ
{\displaystyle \cos \left({\tfrac {\pi }{2}}-\theta \right)=\sin \theta }
cos
(
π
−
θ
)
=
−
cos
θ
{\displaystyle \cos(\pi -\theta )=-\cos \theta }
cos
(
3
π
2
−
θ
)
=
−
sin
θ
{\displaystyle \cos \left({\tfrac {3\pi }{2}}-\theta \right)=-\sin \theta }
cos
(
2
π
−
θ
)
=
+
cos
(
θ
)
=
cos
(
−
θ
)
{\displaystyle \cos(2\pi -\theta )=+\cos(\theta )=\cos(-\theta )}
tan
(
−
θ
)
=
−
tan
θ
{\displaystyle \tan(-\theta )=-\tan \theta }
tan
(
π
2
−
θ
)
=
cot
θ
{\displaystyle \tan \left({\tfrac {\pi }{2}}-\theta \right)=\cot \theta }
tan
(
π
−
θ
)
=
−
tan
θ
{\displaystyle \tan(\pi -\theta )=-\tan \theta }
tan
(
3
π
2
−
θ
)
=
+
cot
θ
{\displaystyle \tan \left({\tfrac {3\pi }{2}}-\theta \right)=+\cot \theta }
tan
(
2
π
−
θ
)
=
−
tan
(
θ
)
=
tan
(
−
θ
)
{\displaystyle \tan(2\pi -\theta )=-\tan(\theta )=\tan(-\theta )}
csc
(
−
θ
)
=
−
csc
θ
{\displaystyle \csc(-\theta )=-\csc \theta }
csc
(
π
2
−
θ
)
=
sec
θ
{\displaystyle \csc \left({\tfrac {\pi }{2}}-\theta \right)=\sec \theta }
csc
(
π
−
θ
)
=
+
csc
θ
{\displaystyle \csc(\pi -\theta )=+\csc \theta }
csc
(
3
π
2
−
θ
)
=
−
sec
θ
{\displaystyle \csc \left({\tfrac {3\pi }{2}}-\theta \right)=-\sec \theta }
csc
(
2
π
−
θ
)
=
−
csc
(
θ
)
=
csc
(
−
θ
)
{\displaystyle \csc(2\pi -\theta )=-\csc(\theta )=\csc(-\theta )}
sec
(
−
θ
)
=
+
sec
θ
{\displaystyle \sec(-\theta )=+\sec \theta }
sec
(
π
2
−
θ
)
=
csc
θ
{\displaystyle \sec \left({\tfrac {\pi }{2}}-\theta \right)=\csc \theta }
sec
(
π
−
θ
)
=
−
sec
θ
{\displaystyle \sec(\pi -\theta )=-\sec \theta }
sec
(
3
π
2
−
θ
)
=
−
csc
θ
{\displaystyle \sec \left({\tfrac {3\pi }{2}}-\theta \right)=-\csc \theta }
sec
(
2
π
−
θ
)
=
+
sec
(
θ
)
=
sec
(
−
θ
)
{\displaystyle \sec(2\pi -\theta )=+\sec(\theta )=\sec(-\theta )}
cot
(
−
θ
)
=
−
cot
θ
{\displaystyle \cot(-\theta )=-\cot \theta }
cot
(
π
2
−
θ
)
=
tan
θ
{\displaystyle \cot \left({\tfrac {\pi }{2}}-\theta \right)=\tan \theta }
cot
(
π
−
θ
)
=
−
cot
θ
{\displaystyle \cot(\pi -\theta )=-\cot \theta }
cot
(
3
π
2
−
θ
)
=
+
tan
θ
{\displaystyle \cot \left({\tfrac {3\pi }{2}}-\theta \right)=+\tan \theta }
cot
(
2
π
−
θ
)
=
−
cot
(
θ
)
=
cot
(
−
θ
)
{\displaystyle \cot(2\pi -\theta )=-\cot(\theta )=\cot(-\theta )}
Shifts and periodicity
Transformation of coordinates (a ,b ) when shifting the angle
θ
{\displaystyle \theta }
π
2
{\displaystyle {\frac {\pi }{2}}}
Shift by one quarter period
Shift by one half period
Shift by full periods[ 4]
Period
sin
(
θ
±
π
2
)
=
±
cos
θ
{\displaystyle \sin(\theta \pm {\tfrac {\pi }{2}})=\pm \cos \theta }
sin
(
θ
+
π
)
=
−
sin
θ
{\displaystyle \sin(\theta +\pi )=-\sin \theta }
sin
(
θ
+
k
⋅
2
π
)
=
+
sin
θ
{\displaystyle \sin(\theta +k\cdot 2\pi )=+\sin \theta }
2
π
{\displaystyle 2\pi }
cos
(
θ
±
π
2
)
=
∓
sin
θ
{\displaystyle \cos(\theta \pm {\tfrac {\pi }{2}})=\mp \sin \theta }
cos
(
θ
+
π
)
=
−
cos
θ
{\displaystyle \cos(\theta +\pi )=-\cos \theta }
cos
(
θ
+
k
⋅
2
π
)
=
+
cos
θ
{\displaystyle \cos(\theta +k\cdot 2\pi )=+\cos \theta }
2
π
{\displaystyle 2\pi }
csc
(
θ
±
π
2
)
=
±
sec
θ
{\displaystyle \csc(\theta \pm {\tfrac {\pi }{2}})=\pm \sec \theta }
csc
(
θ
+
π
)
=
−
csc
θ
{\displaystyle \csc(\theta +\pi )=-\csc \theta }
csc
(
θ
+
k
⋅
2
π
)
=
+
csc
θ
{\displaystyle \csc(\theta +k\cdot 2\pi )=+\csc \theta }
2
π
{\displaystyle 2\pi }
sec
(
θ
±
π
2
)
=
∓
csc
θ
{\displaystyle \sec(\theta \pm {\tfrac {\pi }{2}})=\mp \csc \theta }
sec
(
θ
+
π
)
=
−
sec
θ
{\displaystyle \sec(\theta +\pi )=-\sec \theta }
sec
(
θ
+
k
⋅
2
π
)
=
+
sec
θ
{\displaystyle \sec(\theta +k\cdot 2\pi )=+\sec \theta }
2
π
{\displaystyle 2\pi }
tan
(
θ
±
π
4
)
=
tan
θ
±
1
1
∓
tan
θ
{\displaystyle \tan(\theta \pm {\tfrac {\pi }{4}})={\tfrac {\tan \theta \pm 1}{1\mp \tan \theta }}}
tan
(
θ
+
π
2
)
=
−
cot
θ
{\displaystyle \tan(\theta +{\tfrac {\pi }{2}})=-\cot \theta }
tan
(
θ
+
k
⋅
π
)
=
+
tan
θ
{\displaystyle \tan(\theta +k\cdot \pi )=+\tan \theta }
π
{\displaystyle \pi }
cot
(
θ
±
π
4
)
=
cot
θ
∓
1
1
±
cot
θ
{\displaystyle \cot(\theta \pm {\tfrac {\pi }{4}})={\tfrac {\cot \theta \mp 1}{1\pm \cot \theta }}}
cot
(
θ
+
π
2
)
=
−
tan
θ
{\displaystyle \cot(\theta +{\tfrac {\pi }{2}})=-\tan \theta }
cot
(
θ
+
k
⋅
π
)
=
+
cot
θ
{\displaystyle \cot(\theta +k\cdot \pi )=+\cot \theta }
π
{\displaystyle \pi }
Signs
The sign of trigonometric functions depends on quadrant of the angle. If
−
π
<
θ
≤
π
{\displaystyle {-\pi }<\theta \leq \pi }
sgn is the sign function ,
sgn
(
sin
θ
)
=
sgn
(
csc
θ
)
=
{
+
1
if
0
<
θ
<
π
−
1
if
−
π
<
θ
<
0
0
if
θ
∈
{
0
,
π
}
sgn
(
cos
θ
)
=
sgn
(
sec
θ
)
=
{
+
1
if
−
1
2
π
<
θ
<
1
2
π
−
1
if
−
π
<
θ
<
−
1
2
π
or
1
2
π
<
θ
<
π
0
if
θ
∈
{
−
1
2
π
,
1
2
π
}
sgn
(
tan
θ
)
=
sgn
(
cot
θ
)
=
{
+
1
if
−
π
<
θ
<
−
1
2
π
or
0
<
θ
<
1
2
π
−
1
if
−
1
2
π
<
θ
<
0
or
1
2
π
<
θ
<
π
0
if
θ
∈
{
−
1
2
π
,
0
,
1
2
π
,
π
}
{\displaystyle {\begin{aligned}\operatorname {sgn}(\sin \theta )=\operatorname {sgn}(\csc \theta )&={\begin{cases}+1&{\text{if}}\ \ 0<\theta <\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <0\\0&{\text{if}}\ \ \theta \in \{0,\pi \}\end{cases}}\\[5mu]\operatorname {sgn}(\cos \theta )=\operatorname {sgn}(\sec \theta )&={\begin{cases}+1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },{\tfrac {1}{2}}\pi {\bigr \}}\end{cases}}\\[5mu]\operatorname {sgn}(\tan \theta )=\operatorname {sgn}(\cot \theta )&={\begin{cases}+1&{\text{if}}\ \ {-\pi }<\theta <-{\tfrac {1}{2}}\pi \ \ {\text{or}}\ \ 0<\theta <{\tfrac {1}{2}}\pi \\-1&{\text{if}}\ \ {-{\tfrac {1}{2}}\pi }<\theta <0\ \ {\text{or}}\ \ {\tfrac {1}{2}}\pi <\theta <\pi \\0&{\text{if}}\ \ \theta \in {\bigl \{}{-{\tfrac {1}{2}}\pi },0,{\tfrac {1}{2}}\pi ,\pi {\bigr \}}\end{cases}}\end{aligned}}}
The trigonometric functions are periodic with common period
2
π
,
{\displaystyle 2\pi ,}
θ outside the interval
(
−
π
,
π
]
,
{\displaystyle ({-\pi },\pi ],}
§ Shifts and periodicity above).
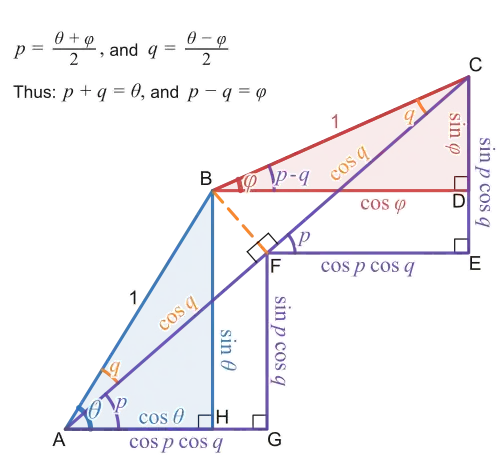
Angle sum and difference identities
Geometric construction to derive angle sum trigonometric identities Diagram showing the angle difference identities for
sin
(
α
−
β
)
{\displaystyle \sin(\alpha -\beta )}
cos
(
α
−
β
)
{\displaystyle \cos(\alpha -\beta )}
These are also known as the angle addition and subtraction theorems (or formulae ).
sin
(
α
+
β
)
=
sin
α
cos
β
+
cos
α
sin
β
sin
(
α
−
β
)
=
sin
α
cos
β
−
cos
α
sin
β
cos
(
α
+
β
)
=
cos
α
cos
β
−
sin
α
sin
β
cos
(
α
−
β
)
=
cos
α
cos
β
+
sin
α
sin
β
{\displaystyle {\begin{aligned}\sin(\alpha +\beta )&=\sin \alpha \cos \beta +\cos \alpha \sin \beta \\\sin(\alpha -\beta )&=\sin \alpha \cos \beta -\cos \alpha \sin \beta \\\cos(\alpha +\beta )&=\cos \alpha \cos \beta -\sin \alpha \sin \beta \\\cos(\alpha -\beta )&=\cos \alpha \cos \beta +\sin \alpha \sin \beta \end{aligned}}}
The angle difference identities for
sin
(
α
−
β
)
{\displaystyle \sin(\alpha -\beta )}
cos
(
α
−
β
)
{\displaystyle \cos(\alpha -\beta )}
−
β
{\displaystyle -\beta }
β
{\displaystyle \beta }
sin
(
−
β
)
=
−
sin
(
β
)
{\displaystyle \sin(-\beta )=-\sin(\beta )}
cos
(
−
β
)
=
cos
(
β
)
{\displaystyle \cos(-\beta )=\cos(\beta )}
These identities are summarized in the first two rows of the following table, which also includes sum and difference identities for the other trigonometric functions.
Sine
sin
(
α
±
β
)
{\displaystyle \sin(\alpha \pm \beta )}
=
{\displaystyle =}
sin
α
cos
β
±
cos
α
sin
β
{\displaystyle \sin \alpha \cos \beta \pm \cos \alpha \sin \beta }
[ 5] [ 6]
Cosine
cos
(
α
±
β
)
{\displaystyle \cos(\alpha \pm \beta )}
=
{\displaystyle =}
cos
α
cos
β
∓
sin
α
sin
β
{\displaystyle \cos \alpha \cos \beta \mp \sin \alpha \sin \beta }
[ 6] [ 7]
Tangent
tan
(
α
±
β
)
{\displaystyle \tan(\alpha \pm \beta )}
=
{\displaystyle =}
tan
α
±
tan
β
1
∓
tan
α
tan
β
{\displaystyle {\frac {\tan \alpha \pm \tan \beta }{1\mp \tan \alpha \tan \beta }}}
[ 6] [ 8]
Cosecant
csc
(
α
±
β
)
{\displaystyle \csc(\alpha \pm \beta )}
=
{\displaystyle =}
sec
α
sec
β
csc
α
csc
β
sec
α
csc
β
±
csc
α
sec
β
{\displaystyle {\frac {\sec \alpha \sec \beta \csc \alpha \csc \beta }{\sec \alpha \csc \beta \pm \csc \alpha \sec \beta }}}
[ 9]
Secant
sec
(
α
±
β
)
{\displaystyle \sec(\alpha \pm \beta )}
=
{\displaystyle =}
sec
α
sec
β
csc
α
csc
β
csc
α
csc
β
∓
sec
α
sec
β
{\displaystyle {\frac {\sec \alpha \sec \beta \csc \alpha \csc \beta }{\csc \alpha \csc \beta \mp \sec \alpha \sec \beta }}}
[ 9]
Cotangent
cot
(
α
±
β
)
{\displaystyle \cot(\alpha \pm \beta )}
=
{\displaystyle =}
cot
α
cot
β
∓
1
cot
β
±
cot
α
{\displaystyle {\frac {\cot \alpha \cot \beta \mp 1}{\cot \beta \pm \cot \alpha }}}
[ 6] [ 10]
Arcsine
arcsin
x
±
arcsin
y
{\displaystyle \arcsin x\pm \arcsin y}
=
{\displaystyle =}
arcsin
(
x
1
−
y
2
±
y
1
−
x
2
y
)
{\displaystyle \arcsin \left(x{\sqrt {1-y^{2}}}\pm y{\sqrt {1-x^{2}{\vphantom {y}}}}\right)}
[ 11]
Arccosine
arccos
x
±
arccos
y
{\displaystyle \arccos x\pm \arccos y}
=
{\displaystyle =}
arccos
(
x
y
∓
(
1
−
x
2
)
(
1
−
y
2
)
)
{\displaystyle \arccos \left(xy\mp {\sqrt {\left(1-x^{2}\right)\left(1-y^{2}\right)}}\right)}
[ 12]
Arctangent
arctan
x
±
arctan
y
{\displaystyle \arctan x\pm \arctan y}
=
{\displaystyle =}
arctan
(
x
±
y
1
∓
x
y
)
{\displaystyle \arctan \left({\frac {x\pm y}{1\mp xy}}\right)}
[ 13]
Arccotangent
arccot
x
±
arccot
y
{\displaystyle \operatorname {arccot} x\pm \operatorname {arccot} y}
=
{\displaystyle =}
arccot
(
x
y
∓
1
y
±
x
)
{\displaystyle \operatorname {arccot} \left({\frac {xy\mp 1}{y\pm x}}\right)}
Sines and cosines of sums of infinitely many angles
When the series
∑
i
=
1
∞
θ
i
{\textstyle \sum _{i=1}^{\infty }\theta _{i}}
converges absolutely then
sin
(
∑
i
=
1
∞
θ
i
)
=
∑
odd
k
≥
1
(
−
1
)
k
−
1
2
∑
A
⊆
{
1
,
2
,
3
,
…
}
|
A
|
=
k
(
∏
i
∈
A
sin
θ
i
∏
i
∉
A
cos
θ
i
)
cos
(
∑
i
=
1
∞
θ
i
)
=
∑
even
k
≥
0
(
−
1
)
k
2
∑
A
⊆
{
1
,
2
,
3
,
…
}
|
A
|
=
k
(
∏
i
∈
A
sin
θ
i
∏
i
∉
A
cos
θ
i
)
.
{\displaystyle {\begin{aligned}{\sin }{\biggl (}\sum _{i=1}^{\infty }\theta _{i}{\biggl )}&=\sum _{{\text{odd}}\ k\geq 1}(-1)^{\frac {k-1}{2}}\!\!\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}{\biggl (}\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}{\biggr )}\\{\cos }{\biggl (}\sum _{i=1}^{\infty }\theta _{i}{\biggr )}&=\sum _{{\text{even}}\ k\geq 0}(-1)^{\frac {k}{2}}\,\sum _{\begin{smallmatrix}A\subseteq \{\,1,2,3,\dots \,\}\\\left|A\right|=k\end{smallmatrix}}{\biggl (}\prod _{i\in A}\sin \theta _{i}\prod _{i\not \in A}\cos \theta _{i}{\biggr )}.\end{aligned}}}
Because the series
∑
i
=
1
∞
θ
i
{\textstyle \sum _{i=1}^{\infty }\theta _{i}}
lim
i
→
∞
θ
i
=
0
,
{\textstyle \lim _{i\to \infty }\theta _{i}=0,}
lim
i
→
∞
sin
θ
i
=
0
,
{\textstyle \lim _{i\to \infty }\sin \theta _{i}=0,}
lim
i
→
∞
cos
θ
i
=
1.
{\textstyle \lim _{i\to \infty }\cos \theta _{i}=1.}
cofinitely many cosine factors. Terms with infinitely many sine factors would necessarily be equal to zero.
When only finitely many of the angles
θ
i
{\displaystyle \theta _{i}}
Tangents and cotangents of sums
Let
e
k
{\displaystyle e_{k}}
k
=
0
,
1
,
2
,
3
,
…
{\displaystyle k=0,1,2,3,\ldots }
k th-degree elementary symmetric polynomial in the variables
x
i
=
tan
θ
i
{\displaystyle x_{i}=\tan \theta _{i}}
i
=
0
,
1
,
2
,
3
,
…
,
{\displaystyle i=0,1,2,3,\ldots ,}
e
0
=
1
e
1
=
∑
i
x
i
=
∑
i
tan
θ
i
e
2
=
∑
i
<
j
x
i
x
j
=
∑
i
<
j
tan
θ
i
tan
θ
j
e
3
=
∑
i
<
j
<
k
x
i
x
j
x
k
=
∑
i
<
j
<
k
tan
θ
i
tan
θ
j
tan
θ
k
⋮
⋮
{\displaystyle {\begin{aligned}e_{0}&=1\\[6pt]e_{1}&=\sum _{i}x_{i}&&=\sum _{i}\tan \theta _{i}\\[6pt]e_{2}&=\sum _{i<j}x_{i}x_{j}&&=\sum _{i<j}\tan \theta _{i}\tan \theta _{j}\\[6pt]e_{3}&=\sum _{i<j<k}x_{i}x_{j}x_{k}&&=\sum _{i<j<k}\tan \theta _{i}\tan \theta _{j}\tan \theta _{k}\\&\ \ \vdots &&\ \ \vdots \end{aligned}}}
Then
tan
(
∑
i
θ
i
)
=
e
1
−
e
3
+
e
5
−
⋯
e
0
−
e
2
+
e
4
−
⋯
.
{\displaystyle \tan {\Bigl (}\sum _{i}\theta _{i}{\Bigr )}={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-e_{2}+e_{4}-\cdots }}.}
tan
(
∑
i
θ
i
)
=
sin
(
∑
i
θ
i
)
/
∏
i
cos
θ
i
cos
(
∑
i
θ
i
)
/
∏
i
cos
θ
i
=
∑
odd
k
≥
1
(
−
1
)
k
−
1
2
∑
A
⊆
{
1
,
2
,
3
,
…
}
|
A
|
=
k
∏
i
∈
A
tan
θ
i
∑
even
k
≥
0
(
−
1
)
k
2
∑
A
⊆
{
1
,
2
,
3
,
…
}
|
A
|
=
k
∏
i
∈
A
tan
θ
i
=
e
1
−
e
3
+
e
5
−
⋯
e
0
−
e
2
+
e
4
−
⋯
cot
(
∑
i
θ
i
)
=
e
0
−
e
2
+
e
4
−
⋯
e
1
−
e
3
+
e
5
−
⋯
{\displaystyle {\begin{aligned}\tan {\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {{\sin }{\bigl (}\sum _{i}\theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}{{\cos }{\bigl (}\sum _{i}\theta _{i}{\bigr )}/\prod _{i}\cos \theta _{i}}}\\[10pt]&={\frac {\displaystyle \sum _{{\text{odd}}\ k\geq 1}(-1)^{\frac {k-1}{2}}\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\\left|A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}{\displaystyle \sum _{{\text{even}}\ k\geq 0}~(-1)^{\frac {k}{2}}~~\sum _{\begin{smallmatrix}A\subseteq \{1,2,3,\dots \}\\\left|A\right|=k\end{smallmatrix}}\prod _{i\in A}\tan \theta _{i}}}={\frac {e_{1}-e_{3}+e_{5}-\cdots }{e_{0}-e_{2}+e_{4}-\cdots }}\\[10pt]\cot {\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {e_{0}-e_{2}+e_{4}-\cdots }{e_{1}-e_{3}+e_{5}-\cdots }}\end{aligned}}}
The number of terms on the right side depends on the number of terms on the left side.
For example:
tan
(
θ
1
+
θ
2
)
=
e
1
e
0
−
e
2
=
x
1
+
x
2
1
−
x
1
x
2
=
tan
θ
1
+
tan
θ
2
1
−
tan
θ
1
tan
θ
2
,
tan
(
θ
1
+
θ
2
+
θ
3
)
=
e
1
−
e
3
e
0
−
e
2
=
(
x
1
+
x
2
+
x
3
)
−
(
x
1
x
2
x
3
)
1
−
(
x
1
x
2
+
x
1
x
3
+
x
2
x
3
)
,
tan
(
θ
1
+
θ
2
+
θ
3
+
θ
4
)
=
e
1
−
e
3
e
0
−
e
2
+
e
4
=
(
x
1
+
x
2
+
x
3
+
x
4
)
−
(
x
1
x
2
x
3
+
x
1
x
2
x
4
+
x
1
x
3
x
4
+
x
2
x
3
x
4
)
1
−
(
x
1
x
2
+
x
1
x
3
+
x
1
x
4
+
x
2
x
3
+
x
2
x
4
+
x
3
x
4
)
+
(
x
1
x
2
x
3
x
4
)
,
{\displaystyle {\begin{aligned}\tan(\theta _{1}+\theta _{2})&={\frac {e_{1}}{e_{0}-e_{2}}}={\frac {x_{1}+x_{2}}{1\ -\ x_{1}x_{2}}}={\frac {\tan \theta _{1}+\tan \theta _{2}}{1\ -\ \tan \theta _{1}\tan \theta _{2}}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}}}={\frac {(x_{1}+x_{2}+x_{3})\ -\ (x_{1}x_{2}x_{3})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3})}},\\[8pt]\tan(\theta _{1}+\theta _{2}+\theta _{3}+\theta _{4})&={\frac {e_{1}-e_{3}}{e_{0}-e_{2}+e_{4}}}\\[8pt]&={\frac {(x_{1}+x_{2}+x_{3}+x_{4})\ -\ (x_{1}x_{2}x_{3}+x_{1}x_{2}x_{4}+x_{1}x_{3}x_{4}+x_{2}x_{3}x_{4})}{1\ -\ (x_{1}x_{2}+x_{1}x_{3}+x_{1}x_{4}+x_{2}x_{3}+x_{2}x_{4}+x_{3}x_{4})\ +\ (x_{1}x_{2}x_{3}x_{4})}},\end{aligned}}}
and so on. The case of only finitely many terms can be proved by mathematical induction .[ 14] [ 15]
Suppose
a
,
b
,
c
,
d
,
p
,
q
∈
R
{\textstyle a,b,c,d,p,q\in \mathbb {R} }
i
=
−
1
{\textstyle i={\sqrt {-1}}}
a
i
+
b
c
i
+
d
=
p
i
+
q
{\displaystyle {\frac {ai+b}{ci+d}}=pi+q}
and let
φ
{\textstyle \varphi }
tan
φ
=
c
/
d
.
{\textstyle \tan \varphi =c/d.}
a
/
c
≠
b
/
d
{\textstyle a/c\neq b/d}
0
/
0
{\textstyle 0/0}
θ
∈
R
{\textstyle \theta \in \mathbb {R} }
[ 16]
a
tan
θ
+
b
c
tan
θ
+
d
=
p
tan
(
θ
−
φ
)
+
q
.
{\displaystyle {\frac {a\tan \theta +b}{c\tan \theta +d}}=p\tan(\theta -\varphi )+q.}
(In case the denominator of this fraction is 0, we take the value of the fraction to be
∞
{\textstyle \infty }
∞
{\textstyle \infty }
+
∞
{\textstyle +\infty }
−
∞
{\textstyle -\infty }
∞
{\textstyle \infty }
R
∪
{
∞
}
{\textstyle \mathbb {R} \cup \{\,\infty \,\}}
From this identity it can be shown to follow quickly that the family of all Cauchy-distributed random variables is closed under linear fractional tranformations, a result known since 1976.[ 17]
Secants and cosecants of sums
sec
(
∑
i
θ
i
)
=
∏
i
sec
θ
i
e
0
−
e
2
+
e
4
−
⋯
csc
(
∑
i
θ
i
)
=
∏
i
sec
θ
i
e
1
−
e
3
+
e
5
−
⋯
{\displaystyle {\begin{aligned}{\sec }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {\prod _{i}\sec \theta _{i}}{e_{0}-e_{2}+e_{4}-\cdots }}\\[8pt]{\csc }{\Bigl (}\sum _{i}\theta _{i}{\Bigr )}&={\frac {\prod _{i}\sec \theta _{i}}{e_{1}-e_{3}+e_{5}-\cdots }}\end{aligned}}}
where
e
k
{\displaystyle e_{k}}
k th-degree elementary symmetric polynomial in the n variables
x
i
=
tan
θ
i
,
{\displaystyle x_{i}=\tan \theta _{i},}
i
=
1
,
…
,
n
,
{\displaystyle i=1,\ldots ,n,}
[ 18]
For example,
sec
(
α
+
β
+
γ
)
=
sec
α
sec
β
sec
γ
1
−
tan
α
tan
β
−
tan
α
tan
γ
−
tan
β
tan
γ
csc
(
α
+
β
+
γ
)
=
sec
α
sec
β
sec
γ
tan
α
+
tan
β
+
tan
γ
−
tan
α
tan
β
tan
γ
.
{\displaystyle {\begin{aligned}\sec(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{1-\tan \alpha \tan \beta -\tan \alpha \tan \gamma -\tan \beta \tan \gamma }}\\[8pt]\csc(\alpha +\beta +\gamma )&={\frac {\sec \alpha \sec \beta \sec \gamma }{\tan \alpha +\tan \beta +\tan \gamma -\tan \alpha \tan \beta \tan \gamma }}.\end{aligned}}}
Diagram illustrating the relation between Ptolemy's theorem and the angle sum trig identity for sine. Ptolemy's theorem states that the sum of the products of the lengths of opposite sides is equal to the product of the lengths of the diagonals. When those side-lengths are expressed in terms of the sin and cos values shown in the figure above, this yields the angle sum trigonometric identity for sine: sin(α + β ) = sin α cos β + cos α sin β . Ptolemy's theorem is important in the history of trigonometric identities, as it is how results equivalent to the sum and difference formulas for sine and cosine were first proved. It states that in a cyclic quadrilateral
A
B
C
D
{\displaystyle ABCD}
[ 19]
By Thales's theorem ,
∠
D
A
B
{\displaystyle \angle DAB}
∠
D
C
B
{\displaystyle \angle DCB}
D
A
B
{\displaystyle DAB}
D
C
B
{\displaystyle DCB}
B
D
¯
{\displaystyle {\overline {BD}}}
A
B
¯
=
sin
α
{\displaystyle {\overline {AB}}=\sin \alpha }
A
D
¯
=
cos
α
{\displaystyle {\overline {AD}}=\cos \alpha }
B
C
¯
=
sin
β
{\displaystyle {\overline {BC}}=\sin \beta }
C
D
¯
=
cos
β
{\displaystyle {\overline {CD}}=\cos \beta }
By the inscribed angle theorem, the central angle subtended by the chord
A
C
¯
{\displaystyle {\overline {AC}}}
∠
A
D
C
{\displaystyle \angle ADC}
2
(
α
+
β
)
{\displaystyle 2(\alpha +\beta )}
α
+
β
{\displaystyle \alpha +\beta }
1
2
{\textstyle {\frac {1}{2}}}
A
C
¯
{\displaystyle {\overline {AC}}}
2
×
1
2
sin
(
α
+
β
)
{\textstyle 2\times {\frac {1}{2}}\sin(\alpha +\beta )}
sin
(
α
+
β
)
{\displaystyle \sin(\alpha +\beta )}
sin
(
α
+
β
)
{\displaystyle \sin(\alpha +\beta )}
When these values are substituted into the statement of Ptolemy's theorem that
|
A
C
¯
|
⋅
|
B
D
¯
|
=
|
A
B
¯
|
⋅
|
C
D
¯
|
+
|
A
D
¯
|
⋅
|
B
C
¯
|
{\displaystyle |{\overline {AC}}|\cdot |{\overline {BD}}|=|{\overline {AB}}|\cdot |{\overline {CD}}|+|{\overline {AD}}|\cdot |{\overline {BC}}|}
sin
(
α
+
β
)
=
sin
α
cos
β
+
cos
α
sin
β
{\displaystyle \sin(\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta }
sin
(
α
−
β
)
{\displaystyle \sin(\alpha -\beta )}
C
D
¯
{\displaystyle {\overline {CD}}}
B
D
¯
{\displaystyle {\overline {BD}}}
[ 19]
Tn is the n th Chebyshev polynomial
cos
(
n
θ
)
=
T
n
(
cos
θ
)
{\displaystyle \cos(n\theta )=T_{n}(\cos \theta )}
[ 20]
de Moivre's formula , i is the imaginary unit
cos
(
n
θ
)
+
i
sin
(
n
θ
)
=
(
cos
θ
+
i
sin
θ
)
n
{\displaystyle \cos(n\theta )+i\sin(n\theta )=(\cos \theta +i\sin \theta )^{n}}
[ 21]
Visual demonstration of the double-angle formula for sine. For the above isosceles triangle with unit sides and angle
2
θ
{\displaystyle 2\theta }
1 / 2 × base × height is calculated in two orientations. When upright, the area is
sin
θ
cos
θ
{\displaystyle \sin \theta \cos \theta }
1
2
sin
2
θ
{\textstyle {\frac {1}{2}}\sin 2\theta }
sin
2
θ
=
2
sin
θ
cos
θ
.
{\displaystyle \sin 2\theta =2\sin \theta \cos \theta .}
Formulae for twice an angle.[ 22]
sin
(
2
θ
)
=
2
sin
θ
cos
θ
=
(
sin
θ
+
cos
θ
)
2
−
1
=
2
tan
θ
1
+
tan
2
θ
{\displaystyle \sin(2\theta )=2\sin \theta \cos \theta =(\sin \theta +\cos \theta )^{2}-1={\frac {2\tan \theta }{1+\tan ^{2}\theta }}}
cos
(
2
θ
)
=
cos
2
θ
−
sin
2
θ
=
2
cos
2
θ
−
1
=
1
−
2
sin
2
θ
=
1
−
tan
2
θ
1
+
tan
2
θ
{\displaystyle \cos(2\theta )=\cos ^{2}\theta -\sin ^{2}\theta =2\cos ^{2}\theta -1=1-2\sin ^{2}\theta ={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}}
tan
(
2
θ
)
=
2
tan
θ
1
−
tan
2
θ
{\displaystyle \tan(2\theta )={\frac {2\tan \theta }{1-\tan ^{2}\theta }}}
cot
(
2
θ
)
=
cot
2
θ
−
1
2
cot
θ
=
1
−
tan
2
θ
2
tan
θ
{\displaystyle \cot(2\theta )={\frac {\cot ^{2}\theta -1}{2\cot \theta }}={\frac {1-\tan ^{2}\theta }{2\tan \theta }}}
sec
(
2
θ
)
=
sec
2
θ
2
−
sec
2
θ
=
1
+
tan
2
θ
1
−
tan
2
θ
{\displaystyle \sec(2\theta )={\frac {\sec ^{2}\theta }{2-\sec ^{2}\theta }}={\frac {1+\tan ^{2}\theta }{1-\tan ^{2}\theta }}}
csc
(
2
θ
)
=
sec
θ
csc
θ
2
=
1
+
tan
2
θ
2
tan
θ
{\displaystyle \csc(2\theta )={\frac {\sec \theta \csc \theta }{2}}={\frac {1+\tan ^{2}\theta }{2\tan \theta }}}
Formulae for triple angles.[ 22]
sin
(
3
θ
)
=
3
sin
θ
−
4
sin
3
θ
=
4
sin
θ
sin
(
π
3
−
θ
)
sin
(
π
3
+
θ
)
{\displaystyle \sin(3\theta )=3\sin \theta -4\sin ^{3}\theta =4\sin \theta \sin \left({\frac {\pi }{3}}-\theta \right)\sin \left({\frac {\pi }{3}}+\theta \right)}
cos
(
3
θ
)
=
4
cos
3
θ
−
3
cos
θ
=
4
cos
θ
cos
(
π
3
−
θ
)
cos
(
π
3
+
θ
)
{\displaystyle \cos(3\theta )=4\cos ^{3}\theta -3\cos \theta =4\cos \theta \cos \left({\frac {\pi }{3}}-\theta \right)\cos \left({\frac {\pi }{3}}+\theta \right)}
tan
(
3
θ
)
=
3
tan
θ
−
tan
3
θ
1
−
3
tan
2
θ
=
tan
θ
tan
(
π
3
−
θ
)
tan
(
π
3
+
θ
)
{\displaystyle \tan(3\theta )={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}=\tan \theta \tan \left({\frac {\pi }{3}}-\theta \right)\tan \left({\frac {\pi }{3}}+\theta \right)}
cot
(
3
θ
)
=
3
cot
θ
−
cot
3
θ
1
−
3
cot
2
θ
{\displaystyle \cot(3\theta )={\frac {3\cot \theta -\cot ^{3}\theta }{1-3\cot ^{2}\theta }}}
sec
(
3
θ
)
=
sec
3
θ
4
−
3
sec
2
θ
{\displaystyle \sec(3\theta )={\frac {\sec ^{3}\theta }{4-3\sec ^{2}\theta }}}
csc
(
3
θ
)
=
csc
3
θ
3
csc
2
θ
−
4
{\displaystyle \csc(3\theta )={\frac {\csc ^{3}\theta }{3\csc ^{2}\theta -4}}}
Formulae for multiple angles.[ 23]
sin
(
n
θ
)
=
∑
k
odd
(
−
1
)
k
−
1
2
(
n
k
)
cos
n
−
k
θ
sin
k
θ
=
sin
θ
∑
i
=
0
(
n
+
1
)
/
2
∑
j
=
0
i
(
−
1
)
i
−
j
(
n
2
i
+
1
)
(
i
j
)
cos
n
−
2
(
i
−
j
)
−
1
θ
=
sin
(
θ
)
⋅
∑
k
=
0
⌊
n
−
1
2
⌋
(
−
1
)
k
⋅
(
2
⋅
cos
(
θ
)
)
n
−
2
k
−
1
⋅
(
n
−
k
−
1
k
)
=
2
(
n
−
1
)
∏
k
=
0
n
−
1
sin
(
k
π
/
n
+
θ
)
{\displaystyle {\begin{aligned}\sin(n\theta )&=\sum _{k{\text{ odd}}}(-1)^{\frac {k-1}{2}}{n \choose k}\cos ^{n-k}\theta \sin ^{k}\theta =\sin \theta \sum _{i=0}^{(n+1)/2}\sum _{j=0}^{i}(-1)^{i-j}{n \choose 2i+1}{i \choose j}\cos ^{n-2(i-j)-1}\theta \\{}&=\sin(\theta )\cdot \sum _{k=0}^{\left\lfloor {\frac {n-1}{2}}\right\rfloor }(-1)^{k}\cdot {(2\cdot \cos(\theta ))}^{n-2k-1}\cdot {n-k-1 \choose k}\\{}&=2^{(n-1)}\prod _{k=0}^{n-1}\sin(k\pi /n+\theta )\end{aligned}}}
cos
(
n
θ
)
=
∑
k
even
(
−
1
)
k
2
(
n
k
)
cos
n
−
k
θ
sin
k
θ
=
∑
i
=
0
n
/
2
∑
j
=
0
i
(
−
1
)
i
−
j
(
n
2
i
)
(
i
j
)
cos
n
−
2
(
i
−
j
)
θ
=
∑
k
=
0
⌊
n
2
⌋
(
−
1
)
k
⋅
(
2
⋅
cos
(
θ
)
)
n
−
2
k
⋅
(
n
−
k
k
)
⋅
n
2
n
−
2
k
{\displaystyle {\begin{aligned}\cos(n\theta )&=\sum _{k{\text{ even}}}(-1)^{\frac {k}{2}}{n \choose k}\cos ^{n-k}\theta \sin ^{k}\theta =\sum _{i=0}^{n/2}\sum _{j=0}^{i}(-1)^{i-j}{n \choose 2i}{i \choose j}\cos ^{n-2(i-j)}\theta \\{}&=\sum _{k=0}^{\left\lfloor {\frac {n}{2}}\right\rfloor }(-1)^{k}\cdot {(2\cdot \cos(\theta ))}^{n-2k}\cdot {n-k \choose k}\cdot {\frac {n}{2n-2k}}\end{aligned}}}
cos
(
(
2
n
+
1
)
θ
)
=
(
−
1
)
n
2
2
n
∏
k
=
0
2
n
cos
(
k
π
/
(
2
n
+
1
)
−
θ
)
{\displaystyle \cos((2n+1)\theta )=(-1)^{n}2^{2n}\prod _{k=0}^{2n}\cos(k\pi /(2n+1)-\theta )}
cos
(
2
n
θ
)
=
(
−
1
)
n
2
2
n
−
1
∏
k
=
0
2
n
−
1
cos
(
(
1
+
2
k
)
π
/
(
4
n
)
−
θ
)
{\displaystyle \cos(2n\theta )=(-1)^{n}2^{2n-1}\prod _{k=0}^{2n-1}\cos((1+2k)\pi /(4n)-\theta )}
tan
(
n
θ
)
=
∑
k
odd
(
−
1
)
k
−
1
2
(
n
k
)
tan
k
θ
∑
k
even
(
−
1
)
k
2
(
n
k
)
tan
k
θ
{\displaystyle \tan(n\theta )={\frac {\sum _{k{\text{ odd}}}(-1)^{\frac {k-1}{2}}{n \choose k}\tan ^{k}\theta }{\sum _{k{\text{ even}}}(-1)^{\frac {k}{2}}{n \choose k}\tan ^{k}\theta }}}
Chebyshev method
The Chebyshev method is a recursive algorithm for finding the n th multiple angle formula knowing the
(
n
−
1
)
{\displaystyle (n-1)}
(
n
−
2
)
{\displaystyle (n-2)}
[ 24]
cos
(
n
x
)
{\displaystyle \cos(nx)}
cos
(
(
n
−
1
)
x
)
{\displaystyle \cos((n-1)x)}
cos
(
(
n
−
2
)
x
)
{\displaystyle \cos((n-2)x)}
cos
(
x
)
{\displaystyle \cos(x)}
cos
(
n
x
)
=
2
cos
x
cos
(
(
n
−
1
)
x
)
−
cos
(
(
n
−
2
)
x
)
.
{\displaystyle \cos(nx)=2\cos x\cos((n-1)x)-\cos((n-2)x).}
This can be proved by adding together the formulae
cos
(
(
n
−
1
)
x
+
x
)
=
cos
(
(
n
−
1
)
x
)
cos
x
−
sin
(
(
n
−
1
)
x
)
sin
x
cos
(
(
n
−
1
)
x
−
x
)
=
cos
(
(
n
−
1
)
x
)
cos
x
+
sin
(
(
n
−
1
)
x
)
sin
x
{\displaystyle {\begin{aligned}\cos((n-1)x+x)&=\cos((n-1)x)\cos x-\sin((n-1)x)\sin x\\\cos((n-1)x-x)&=\cos((n-1)x)\cos x+\sin((n-1)x)\sin x\end{aligned}}}
It follows by induction that
cos
(
n
x
)
{\displaystyle \cos(nx)}
cos
x
,
{\displaystyle \cos x,}
Chebyshev polynomials#Trigonometric definition .
Similarly,
sin
(
n
x
)
{\displaystyle \sin(nx)}
sin
(
(
n
−
1
)
x
)
,
{\displaystyle \sin((n-1)x),}
sin
(
(
n
−
2
)
x
)
,
{\displaystyle \sin((n-2)x),}
cos
x
{\displaystyle \cos x}
sin
(
n
x
)
=
2
cos
x
sin
(
(
n
−
1
)
x
)
−
sin
(
(
n
−
2
)
x
)
{\displaystyle \sin(nx)=2\cos x\sin((n-1)x)-\sin((n-2)x)}
sin
(
(
n
−
1
)
x
+
x
)
{\displaystyle \sin((n-1)x+x)}
sin
(
(
n
−
1
)
x
−
x
)
.
{\displaystyle \sin((n-1)x-x).}
Serving a purpose similar to that of the Chebyshev method, for the tangent we can write:
tan
(
n
x
)
=
tan
(
(
n
−
1
)
x
)
+
tan
x
1
−
tan
(
(
n
−
1
)
x
)
tan
x
.
{\displaystyle \tan(nx)={\frac {\tan((n-1)x)+\tan x}{1-\tan((n-1)x)\tan x}}\,.}
sin
θ
2
=
sgn
(
sin
θ
2
)
1
−
cos
θ
2
cos
θ
2
=
sgn
(
cos
θ
2
)
1
+
cos
θ
2
tan
θ
2
=
1
−
cos
θ
sin
θ
=
sin
θ
1
+
cos
θ
=
csc
θ
−
cot
θ
=
tan
θ
1
+
sec
θ
=
sgn
(
sin
θ
)
1
−
cos
θ
1
+
cos
θ
=
−
1
+
sgn
(
cos
θ
)
1
+
tan
2
θ
tan
θ
cot
θ
2
=
1
+
cos
θ
sin
θ
=
sin
θ
1
−
cos
θ
=
csc
θ
+
cot
θ
=
sgn
(
sin
θ
)
1
+
cos
θ
1
−
cos
θ
sec
θ
2
=
sgn
(
cos
θ
2
)
2
1
+
cos
θ
csc
θ
2
=
sgn
(
sin
θ
2
)
2
1
−
cos
θ
{\displaystyle {\begin{aligned}\sin {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {1-\cos \theta }{2}}}\\[3pt]\cos {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {1+\cos \theta }{2}}}\\[3pt]\tan {\frac {\theta }{2}}&={\frac {1-\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1+\cos \theta }}=\csc \theta -\cot \theta ={\frac {\tan \theta }{1+\sec {\theta }}}\\[6mu]&=\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}={\frac {-1+\operatorname {sgn}(\cos \theta ){\sqrt {1+\tan ^{2}\theta }}}{\tan \theta }}\\[3pt]\cot {\frac {\theta }{2}}&={\frac {1+\cos \theta }{\sin \theta }}={\frac {\sin \theta }{1-\cos \theta }}=\csc \theta +\cot \theta =\operatorname {sgn}(\sin \theta ){\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}\\\sec {\frac {\theta }{2}}&=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1+\cos \theta }}}\\\csc {\frac {\theta }{2}}&=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {2}{1-\cos \theta }}}\\\end{aligned}}}
[ 25] [ 26]
Also
tan
η
±
θ
2
=
sin
η
±
sin
θ
cos
η
+
cos
θ
tan
(
θ
2
+
π
4
)
=
sec
θ
+
tan
θ
1
−
sin
θ
1
+
sin
θ
=
|
1
−
tan
θ
2
|
|
1
+
tan
θ
2
|
{\displaystyle {\begin{aligned}\tan {\frac {\eta \pm \theta }{2}}&={\frac {\sin \eta \pm \sin \theta }{\cos \eta +\cos \theta }}\\[3pt]\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)&=\sec \theta +\tan \theta \\[3pt]{\sqrt {\frac {1-\sin \theta }{1+\sin \theta }}}&={\frac {\left|1-\tan {\frac {\theta }{2}}\right|}{\left|1+\tan {\frac {\theta }{2}}\right|}}\end{aligned}}}
Table
These can be shown by using either the sum and difference identities or the multiple-angle formulae.
Sine
Cosine
Tangent
Cotangent
Double-angle formula[ 27] [ 28]
sin
(
2
θ
)
=
2
sin
θ
cos
θ
=
2
tan
θ
1
+
tan
2
θ
{\displaystyle {\begin{aligned}\sin(2\theta )&=2\sin \theta \cos \theta \ \\&={\frac {2\tan \theta }{1+\tan ^{2}\theta }}\end{aligned}}}
cos
(
2
θ
)
=
cos
2
θ
−
sin
2
θ
=
2
cos
2
θ
−
1
=
1
−
2
sin
2
θ
=
1
−
tan
2
θ
1
+
tan
2
θ
{\displaystyle {\begin{aligned}\cos(2\theta )&=\cos ^{2}\theta -\sin ^{2}\theta \\&=2\cos ^{2}\theta -1\\&=1-2\sin ^{2}\theta \\&={\frac {1-\tan ^{2}\theta }{1+\tan ^{2}\theta }}\end{aligned}}}
tan
(
2
θ
)
=
2
tan
θ
1
−
tan
2
θ
{\displaystyle \tan(2\theta )={\frac {2\tan \theta }{1-\tan ^{2}\theta }}}
cot
(
2
θ
)
=
cot
2
θ
−
1
2
cot
θ
{\displaystyle \cot(2\theta )={\frac {\cot ^{2}\theta -1}{2\cot \theta }}}
Triple-angle formula[ 20] [ 29]
sin
(
3
θ
)
=
−
sin
3
θ
+
3
cos
2
θ
sin
θ
=
−
4
sin
3
θ
+
3
sin
θ
{\displaystyle {\begin{aligned}\sin(3\theta )&=-\sin ^{3}\theta +3\cos ^{2}\theta \sin \theta \\&=-4\sin ^{3}\theta +3\sin \theta \end{aligned}}}
cos
(
3
θ
)
=
cos
3
θ
−
3
sin
2
θ
cos
θ
=
4
cos
3
θ
−
3
cos
θ
{\displaystyle {\begin{aligned}\cos(3\theta )&=\cos ^{3}\theta -3\sin ^{2}\theta \cos \theta \\&=4\cos ^{3}\theta -3\cos \theta \end{aligned}}}
tan
(
3
θ
)
=
3
tan
θ
−
tan
3
θ
1
−
3
tan
2
θ
{\displaystyle \tan(3\theta )={\frac {3\tan \theta -\tan ^{3}\theta }{1-3\tan ^{2}\theta }}}
cot
(
3
θ
)
=
3
cot
θ
−
cot
3
θ
1
−
3
cot
2
θ
{\displaystyle \cot(3\theta )={\frac {3\cot \theta -\cot ^{3}\theta }{1-3\cot ^{2}\theta }}}
Half-angle formula[ 25] [ 26]
sin
θ
2
=
sgn
(
sin
θ
2
)
1
−
cos
θ
2
(
or
sin
2
θ
2
=
1
−
cos
θ
2
)
{\displaystyle {\begin{aligned}&\sin {\frac {\theta }{2}}=\operatorname {sgn} \left(\sin {\frac {\theta }{2}}\right){\sqrt {\frac {1-\cos \theta }{2}}}\\\\&\left({\text{or }}\sin ^{2}{\frac {\theta }{2}}={\frac {1-\cos \theta }{2}}\right)\end{aligned}}}
cos
θ
2
=
sgn
(
cos
θ
2
)
1
+
cos
θ
2
(
or
cos
2
θ
2
=
1
+
cos
θ
2
)
{\displaystyle {\begin{aligned}&\cos {\frac {\theta }{2}}=\operatorname {sgn} \left(\cos {\frac {\theta }{2}}\right){\sqrt {\frac {1+\cos \theta }{2}}}\\\\&\left({\text{or }}\cos ^{2}{\frac {\theta }{2}}={\frac {1+\cos \theta }{2}}\right)\end{aligned}}}
tan
θ
2
=
csc
θ
−
cot
θ
=
±
1
−
cos
θ
1
+
cos
θ
=
sin
θ
1
+
cos
θ
=
1
−
cos
θ
sin
θ
tan
η
+
θ
2
=
sin
η
+
sin
θ
cos
η
+
cos
θ
tan
(
θ
2
+
π
4
)
=
sec
θ
+
tan
θ
1
−
sin
θ
1
+
sin
θ
=
|
1
−
tan
θ
2
|
|
1
+
tan
θ
2
|
tan
θ
2
=
tan
θ
1
+
1
+
tan
2
θ
for
θ
∈
(
−
π
2
,
π
2
)
{\displaystyle {\begin{aligned}\tan {\frac {\theta }{2}}&=\csc \theta -\cot \theta \\&=\pm \,{\sqrt {\frac {1-\cos \theta }{1+\cos \theta }}}\\[3pt]&={\frac {\sin \theta }{1+\cos \theta }}\\[3pt]&={\frac {1-\cos \theta }{\sin \theta }}\\[5pt]\tan {\frac {\eta +\theta }{2}}&={\frac {\sin \eta +\sin \theta }{\cos \eta +\cos \theta }}\\[5pt]\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)&=\sec \theta +\tan \theta \\[5pt]{\sqrt {\frac {1-\sin \theta }{1+\sin \theta }}}&={\frac {\left|1-\tan {\frac {\theta }{2}}\right|}{\left|1+\tan {\frac {\theta }{2}}\right|}}\\[5pt]\tan {\frac {\theta }{2}}&={\frac {\tan \theta }{1+{\sqrt {1+\tan ^{2}\theta }}}}\\&{\text{for }}\theta \in \left(-{\tfrac {\pi }{2}},{\tfrac {\pi }{2}}\right)\end{aligned}}}
cot
θ
2
=
csc
θ
+
cot
θ
=
±
1
+
cos
θ
1
−
cos
θ
=
sin
θ
1
−
cos
θ
=
1
+
cos
θ
sin
θ
{\displaystyle {\begin{aligned}\cot {\frac {\theta }{2}}&=\csc \theta +\cot \theta \\&=\pm \,{\sqrt {\frac {1+\cos \theta }{1-\cos \theta }}}\\[3pt]&={\frac {\sin \theta }{1-\cos \theta }}\\[4pt]&={\frac {1+\cos \theta }{\sin \theta }}\end{aligned}}}
The fact that the triple-angle formula for sine and cosine only involves powers of a single function allows one to relate the geometric problem of a compass and straightedge construction of angle trisection to the algebraic problem of solving a cubic equation , which allows one to prove that trisection is in general impossible using the given tools.
A formula for computing the trigonometric identities for the one-third angle exists, but it requires finding the zeroes of the cubic equation 4x 3 − 3x + d = 0 , where
x
{\displaystyle x}
d is the known value of the cosine function at the full angle. However, the discriminant of this equation is positive, so this equation has three real roots (of which only one is the solution for the cosine of the one-third angle). None of these solutions are reducible to a real algebraic expression , as they use intermediate complex numbers under the cube roots .
Obtained by solving the second and third versions of the cosine double-angle formula.
Sine
Cosine
Other
sin
2
θ
=
1
−
cos
(
2
θ
)
2
{\displaystyle \sin ^{2}\theta ={\frac {1-\cos(2\theta )}{2}}}
cos
2
θ
=
1
+
cos
(
2
θ
)
2
{\displaystyle \cos ^{2}\theta ={\frac {1+\cos(2\theta )}{2}}}
sin
2
θ
cos
2
θ
=
1
−
cos
(
4
θ
)
8
{\displaystyle \sin ^{2}\theta \cos ^{2}\theta ={\frac {1-\cos(4\theta )}{8}}}
sin
3
θ
=
3
sin
θ
−
sin
(
3
θ
)
4
{\displaystyle \sin ^{3}\theta ={\frac {3\sin \theta -\sin(3\theta )}{4}}}
cos
3
θ
=
3
cos
θ
+
cos
(
3
θ
)
4
{\displaystyle \cos ^{3}\theta ={\frac {3\cos \theta +\cos(3\theta )}{4}}}
sin
3
θ
cos
3
θ
=
3
sin
(
2
θ
)
−
sin
(
6
θ
)
32
{\displaystyle \sin ^{3}\theta \cos ^{3}\theta ={\frac {3\sin(2\theta )-\sin(6\theta )}{32}}}
sin
4
θ
=
3
−
4
cos
(
2
θ
)
+
cos
(
4
θ
)
8
{\displaystyle \sin ^{4}\theta ={\frac {3-4\cos(2\theta )+\cos(4\theta )}{8}}}
cos
4
θ
=
3
+
4
cos
(
2
θ
)
+
cos
(
4
θ
)
8
{\displaystyle \cos ^{4}\theta ={\frac {3+4\cos(2\theta )+\cos(4\theta )}{8}}}
sin
4
θ
cos
4
θ
=
3
−
4
cos
(
4
θ
)
+
cos
(
8
θ
)
128
{\displaystyle \sin ^{4}\theta \cos ^{4}\theta ={\frac {3-4\cos(4\theta )+\cos(8\theta )}{128}}}
sin
5
θ
=
10
sin
θ
−
5
sin
(
3
θ
)
+
sin
(
5
θ
)
16
{\displaystyle \sin ^{5}\theta ={\frac {10\sin \theta -5\sin(3\theta )+\sin(5\theta )}{16}}}
cos
5
θ
=
10
cos
θ
+
5
cos
(
3
θ
)
+
cos
(
5
θ
)
16
{\displaystyle \cos ^{5}\theta ={\frac {10\cos \theta +5\cos(3\theta )+\cos(5\theta )}{16}}}
sin
5
θ
cos
5
θ
=
10
sin
(
2
θ
)
−
5
sin
(
6
θ
)
+
sin
(
10
θ
)
512
{\displaystyle \sin ^{5}\theta \cos ^{5}\theta ={\frac {10\sin(2\theta )-5\sin(6\theta )+\sin(10\theta )}{512}}}
Cosine power-reduction formula: an illustrative diagram. The red, orange and blue triangles are all similar, and the red and orange triangles are congruent. The hypotenuse
A
D
¯
{\displaystyle {\overline {AD}}}
2
cos
θ
{\displaystyle 2\cos \theta }
∠
D
A
E
{\displaystyle \angle DAE}
θ
{\displaystyle \theta }
A
E
¯
{\displaystyle {\overline {AE}}}
2
cos
2
θ
{\displaystyle 2\cos ^{2}\theta }
B
D
¯
{\displaystyle {\overline {BD}}}
A
F
¯
{\displaystyle {\overline {AF}}}
1
+
cos
(
2
θ
)
{\displaystyle 1+\cos(2\theta )}
2
cos
2
θ
=
1
+
cos
(
2
θ
)
{\displaystyle 2\cos ^{2}\theta =1+\cos(2\theta )}
2
{\displaystyle 2}
cos
2
θ
=
{\displaystyle \cos ^{2}\theta =}
1
2
(
1
+
cos
(
2
θ
)
)
{\textstyle {\frac {1}{2}}(1+\cos(2\theta ))}
θ
{\displaystyle \theta }
θ
/
2
{\displaystyle \theta /2}
cos
(
θ
/
2
)
=
±
(
1
+
cos
θ
)
/
2
.
{\textstyle \cos \left(\theta /2\right)=\pm {\sqrt {\left(1+\cos \theta \right)/2}}.}
Sine power-reduction formula: an illustrative diagram. The shaded blue and green triangles, and the red-outlined triangle
E
B
D
{\displaystyle EBD}
θ
{\displaystyle \theta }
B
D
¯
{\displaystyle {\overline {BD}}}
2
sin
θ
{\displaystyle 2\sin \theta }
D
E
¯
{\displaystyle {\overline {DE}}}
2
sin
2
θ
{\displaystyle 2\sin ^{2}\theta }
A
E
¯
{\displaystyle {\overline {AE}}}
cos
2
θ
{\displaystyle \cos 2\theta }
A
E
¯
{\displaystyle {\overline {AE}}}
D
E
¯
{\displaystyle {\overline {DE}}}
A
D
¯
{\displaystyle {\overline {AD}}}
cos
2
θ
+
2
sin
2
θ
=
1
{\displaystyle \cos 2\theta +2\sin ^{2}\theta =1}
cos
2
θ
{\displaystyle \cos 2\theta }
sin
2
θ
=
{\displaystyle \sin ^{2}\theta =}
1
2
(
1
−
cos
(
2
θ
)
)
{\textstyle {\frac {1}{2}}(1-\cos(2\theta ))}
θ
{\displaystyle \theta }
θ
/
2
{\displaystyle \theta /2}
sin
(
θ
/
2
)
=
±
(
1
−
cos
θ
)
/
2
.
{\textstyle \sin \left(\theta /2\right)=\pm {\sqrt {\left(1-\cos \theta \right)/2}}.}
E
B
¯
{\displaystyle {\overline {EB}}}
sin
2
θ
=
2
sin
θ
cos
θ
{\displaystyle \sin 2\theta =2\sin \theta \cos \theta }
In general terms of powers of
sin
θ
{\displaystyle \sin \theta }
cos
θ
{\displaystyle \cos \theta }
De Moivre's formula , Euler's formula and the binomial theorem .
if n is ...
cos
n
θ
{\displaystyle \cos ^{n}\theta }
sin
n
θ
{\displaystyle \sin ^{n}\theta }
n is odd
cos
n
θ
=
2
2
n
∑
k
=
0
n
−
1
2
(
n
k
)
cos
(
(
n
−
2
k
)
θ
)
{\displaystyle \cos ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}{\binom {n}{k}}\cos {{\big (}(n-2k)\theta {\big )}}}
sin
n
θ
=
2
2
n
∑
k
=
0
n
−
1
2
(
−
1
)
(
n
−
1
2
−
k
)
(
n
k
)
sin
(
(
n
−
2
k
)
θ
)
{\displaystyle \sin ^{n}\theta ={\frac {2}{2^{n}}}\sum _{k=0}^{\frac {n-1}{2}}(-1)^{\left({\frac {n-1}{2}}-k\right)}{\binom {n}{k}}\sin {{\big (}(n-2k)\theta {\big )}}}
n is even
cos
n
θ
=
1
2
n
(
n
n
2
)
+
2
2
n
∑
k
=
0
n
2
−
1
(
n
k
)
cos
(
(
n
−
2
k
)
θ
)
{\displaystyle \cos ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}{\binom {n}{k}}\cos {{\big (}(n-2k)\theta {\big )}}}
sin
n
θ
=
1
2
n
(
n
n
2
)
+
2
2
n
∑
k
=
0
n
2
−
1
(
−
1
)
(
n
2
−
k
)
(
n
k
)
cos
(
(
n
−
2
k
)
θ
)
{\displaystyle \sin ^{n}\theta ={\frac {1}{2^{n}}}{\binom {n}{\frac {n}{2}}}+{\frac {2}{2^{n}}}\sum _{k=0}^{{\frac {n}{2}}-1}(-1)^{\left({\frac {n}{2}}-k\right)}{\binom {n}{k}}\cos {{\big (}(n-2k)\theta {\big )}}}
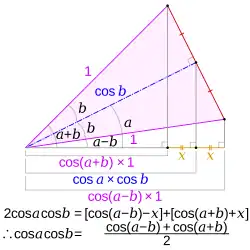
Product-to-sum and sum-to-product identities
Proof of the sum-and-difference-to-product cosine identity for prosthaphaeresis calculations using an isosceles triangle The product-to-sum identities[ 30] prosthaphaeresis formulae can be proven by expanding their right-hand sides using the angle addition theorems . Historically, the first four of these were known as Werner's formulas , after Johannes Werner who used them for astronomical calculations.[ 31] amplitude modulation for an application of the product-to-sum formulae, and beat (acoustics) and phase detector for applications of the sum-to-product formulae.
Product-to-sum identities
The product of two sines or cosines of different angles can be converted to a sum of trigonometric functions of a sum and difference of those angles:
cos
θ
cos
φ
=
1
2
(
cos
(
θ
−
φ
)
+
cos
(
θ
+
φ
)
)
,
sin
θ
sin
φ
=
1
2
(
cos
(
θ
−
φ
)
−
cos
(
θ
+
φ
)
)
,
sin
θ
cos
φ
=
1
2
(
sin
(
θ
+
φ
)
+
sin
(
θ
−
φ
)
)
,
cos
θ
sin
φ
=
1
2
(
sin
(
θ
+
φ
)
−
sin
(
θ
−
φ
)
)
.
{\displaystyle {\begin{aligned}\cos \theta \,\cos \varphi &={\tfrac {1}{2}}{\bigl (}\!\!~\cos(\theta -\varphi )+\cos(\theta +\varphi ){\bigr )},\\[5mu]\sin \theta \,\sin \varphi &={\tfrac {1}{2}}{\bigl (}\!\!~\cos(\theta -\varphi )-\cos(\theta +\varphi ){\bigr )},\\[5mu]\sin \theta \,\cos \varphi &={\tfrac {1}{2}}{\bigl (}\!\!~\sin(\theta +\varphi )+\sin(\theta -\varphi ){\bigr )},\\[5mu]\cos \theta \,\sin \varphi &={\tfrac {1}{2}}{\bigl (}\!\!~\sin(\theta +\varphi )-\sin(\theta -\varphi ){\bigr )}.\end{aligned}}}
tan
θ
tan
φ
=
cos
(
θ
−
φ
)
−
cos
(
θ
+
φ
)
cos
(
θ
−
φ
)
+
cos
(
θ
+
φ
)
,
tan
θ
tan
φ
=
sin
(
θ
+
φ
)
+
sin
(
θ
−
φ
)
sin
(
θ
+
φ
)
−
sin
(
θ
−
φ
)
.
{\displaystyle {\begin{aligned}\tan \theta \,\tan \varphi &={\frac {\cos(\theta -\varphi )-\cos(\theta +\varphi )}{\cos(\theta -\varphi )+\cos(\theta +\varphi )}},\\[5mu]{\frac {\tan \theta }{\tan \varphi }}&={\frac {\sin(\theta +\varphi )+\sin(\theta -\varphi )}{\sin(\theta +\varphi )-\sin(\theta -\varphi )}}.\end{aligned}}}
More generally, for a product of any number of sines or cosines,
∏
k
=
1
n
cos
θ
k
=
1
2
n
∑
e
∈
S
cos
(
e
1
θ
1
+
⋯
+
e
n
θ
n
)
where
e
=
(
e
1
,
…
,
e
n
)
∈
S
=
{
1
,
−
1
}
n
,
∏
k
=
1
n
sin
θ
k
=
(
−
1
)
⌊
n
2
⌋
2
n
{
∑
e
∈
S
cos
(
e
1
θ
1
+
⋯
+
e
n
θ
n
)
∏
j
=
1
n
e
j
if
n
is even
,
∑
e
∈
S
sin
(
e
1
θ
1
+
⋯
+
e
n
θ
n
)
∏
j
=
1
n
e
j
if
n
is odd
.
{\displaystyle {\begin{aligned}\prod _{k=1}^{n}\cos \theta _{k}&={\frac {1}{2^{n}}}\sum _{e\in S}\cos(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n})\\[5mu]&{\text{where }}e=(e_{1},\ldots ,e_{n})\in S=\{1,-1\}^{n},\\\prod _{k=1}^{n}\sin \theta _{k}&={\frac {(-1)^{\left\lfloor {\frac {n}{2}}\right\rfloor }}{2^{n}}}{\begin{cases}\displaystyle \sum _{e\in S}\cos(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n})\prod _{j=1}^{n}e_{j}\;{\text{if}}\;n\;{\text{is even}},\\\displaystyle \sum _{e\in S}\sin(e_{1}\theta _{1}+\cdots +e_{n}\theta _{n})\prod _{j=1}^{n}e_{j}\;{\text{if}}\;n\;{\text{is odd}}.\end{cases}}\end{aligned}}}
Sum-to-product identities
Diagram illustrating sum-to-product identities for sine and cosine. The blue right-angled triangle has angle
θ
{\displaystyle \theta }
φ
{\displaystyle \varphi }
p
{\displaystyle p}
q
{\displaystyle q}
p
=
1
2
(
θ
+
φ
)
{\displaystyle p={\tfrac {1}{2}}(\theta +\varphi )}
q
=
1
2
(
θ
−
φ
)
{\displaystyle q={\tfrac {1}{2}}(\theta -\varphi )}
θ
=
p
+
q
{\displaystyle \theta =p+q}
φ
=
p
−
q
{\displaystyle \varphi =p-q}
A
F
G
{\displaystyle AFG}
F
C
E
{\displaystyle FCE}
cos
q
{\displaystyle \cos q}
p
{\displaystyle p}
sin
θ
+
sin
φ
{\displaystyle \sin \theta +\sin \varphi }
2
sin
p
cos
q
{\displaystyle 2\sin p\cos q}
p
{\displaystyle p}
q
{\displaystyle q}
θ
{\displaystyle \theta }
φ
{\displaystyle \varphi }
sin
θ
+
sin
φ
=
2
sin
1
2
(
θ
+
φ
)
cos
1
2
(
θ
−
φ
)
{\displaystyle \sin \theta +\sin \varphi =2\sin {\tfrac {1}{2}}(\theta +\varphi )\,\cos {\tfrac {1}{2}}(\theta -\varphi )}
The sum of sines or cosines of two angles can be converted to a product of sines or cosines of the mean and half the difference of the angles:[ 32]
sin
θ
+
sin
φ
=
2
sin
1
2
(
θ
+
φ
)
cos
1
2
(
θ
−
φ
)
,
sin
θ
−
sin
φ
=
2
cos
1
2
(
θ
+
φ
)
sin
1
2
(
θ
−
φ
)
,
cos
θ
+
cos
φ
=
2
cos
1
2
(
θ
+
φ
)
cos
1
2
(
θ
−
φ
)
,
cos
θ
−
cos
φ
=
−
2
sin
1
2
(
θ
+
φ
)
sin
1
2
(
θ
−
φ
)
.
{\displaystyle {\begin{aligned}\sin \theta +\sin \varphi &=2\sin {\tfrac {1}{2}}(\theta +\varphi )\,\cos {\tfrac {1}{2}}(\theta -\varphi ),\\[5mu]\sin \theta -\sin \varphi &=2\cos {\tfrac {1}{2}}(\theta +\varphi )\,\sin {\tfrac {1}{2}}(\theta -\varphi ),\\[5mu]\cos \theta +\cos \varphi &=2\cos {\tfrac {1}{2}}(\theta +\varphi )\,\cos {\tfrac {1}{2}}(\theta -\varphi ),\\[5mu]\cos \theta -\cos \varphi &=-2\sin {\tfrac {1}{2}}(\theta +\varphi )\,\sin {\tfrac {1}{2}}(\theta -\varphi ).\end{aligned}}}
The sum of the tangent of two angles can be converted to a quotient of the sine of angles divided by the product of the cosines:[ 32]
tan
θ
±
tan
φ
=
sin
(
θ
±
φ
)
cos
θ
cos
φ
.
{\displaystyle \tan \theta \pm \tan \varphi ={\frac {\sin(\theta \pm \varphi )}{\cos \theta \,\cos \varphi }}.}
Charles Hermite demonstrated the following identity.[ 33]
a
1
,
…
,
a
n
{\displaystyle a_{1},\ldots ,a_{n}}
complex numbers , no two of which differ by an integer multiple of π . Let
A
n
,
k
=
∏
1
≤
j
≤
n
j
≠
k
cot
(
a
k
−
a
j
)
{\displaystyle A_{n,k}=\prod _{\begin{smallmatrix}1\leq j\leq n\\j\neq k\end{smallmatrix}}\cot(a_{k}-a_{j})}
(in particular,
A
1
,
1
,
{\displaystyle A_{1,1},}
empty product , is 1). Then
cot
(
z
−
a
1
)
⋯
cot
(
z
−
a
n
)
=
cos
n
π
2
+
∑
k
=
1
n
A
n
,
k
cot
(
z
−
a
k
)
.
{\displaystyle \cot(z-a_{1})\cdots \cot(z-a_{n})=\cos {\frac {n\pi }{2}}+\sum _{k=1}^{n}A_{n,k}\cot(z-a_{k}).}
The simplest non-trivial example is the case n = 2
cot
(
z
−
a
1
)
cot
(
z
−
a
2
)
=
−
1
+
cot
(
a
1
−
a
2
)
cot
(
z
−
a
1
)
+
cot
(
a
2
−
a
1
)
cot
(
z
−
a
2
)
.
{\displaystyle \cot(z-a_{1})\cot(z-a_{2})=-1+\cot(a_{1}-a_{2})\cot(z-a_{1})+\cot(a_{2}-a_{1})\cot(z-a_{2}).}
Finite products of trigonometric functions
For coprime integers n , m
∏
k
=
1
n
(
2
a
+
2
cos
(
2
π
k
m
n
+
x
)
)
=
2
(
T
n
(
a
)
+
(
−
1
)
n
+
m
cos
(
n
x
)
)
{\displaystyle \prod _{k=1}^{n}\left(2a+2\cos \left({\frac {2\pi km}{n}}+x\right)\right)=2\left(T_{n}(a)+{(-1)}^{n+m}\cos(nx)\right)}
where Tn is the Chebyshev polynomial .
The following relationship holds for the sine function
∏
k
=
1
n
−
1
sin
(
k
π
n
)
=
n
2
n
−
1
.
{\displaystyle \prod _{k=1}^{n-1}\sin \left({\frac {k\pi }{n}}\right)={\frac {n}{2^{n-1}}}.}
More generally for an integer n > 0[ 34]
sin
(
n
x
)
=
2
n
−
1
∏
k
=
0
n
−
1
sin
(
k
n
π
+
x
)
=
2
n
−
1
∏
k
=
1
n
sin
(
k
n
π
−
x
)
.
{\displaystyle \sin(nx)=2^{n-1}\prod _{k=0}^{n-1}\sin \left({\frac {k}{n}}\pi +x\right)=2^{n-1}\prod _{k=1}^{n}\sin \left({\frac {k}{n}}\pi -x\right).}
or written in terms of the chord function
crd
x
≡
2
sin
1
2
x
{\textstyle \operatorname {crd} x\equiv 2\sin {\tfrac {1}{2}}x}
crd
(
n
x
)
=
∏
k
=
1
n
crd
(
k
n
2
π
−
x
)
.
{\displaystyle \operatorname {crd} (nx)=\prod _{k=1}^{n}\operatorname {crd} \left({\frac {k}{n}}2\pi -x\right).}
This comes from the factorization of the polynomial
z
n
−
1
{\textstyle z^{n}-1}
root of unity ): For any complex z and an integer n > 0
z
n
−
1
=
∏
k
=
1
n
(
z
−
exp
(
k
n
2
π
i
)
)
.
{\displaystyle z^{n}-1=\prod _{k=1}^{n}\left(z-\exp {\Bigl (}{\frac {k}{n}}2\pi i{\Bigr )}\right).}
Linear combinations
For some purposes it is important to know that any linear combination of sine waves of the same period or frequency but different phase shifts is also a sine wave with the same period or frequency, but a different phase shift. This is useful in sinusoid data fitting , because the measured or observed data are linearly related to the a and b unknowns of the in-phase and quadrature components basis below, resulting in a simpler Jacobian , compared to that of
c
{\displaystyle c}
φ
{\displaystyle \varphi }
Sine and cosine
The linear combination, or harmonic addition, of sine and cosine waves is equivalent to a single sine wave with a phase shift and scaled amplitude,[ 35] [ 36]
a
cos
x
+
b
sin
x
=
c
cos
(
x
+
φ
)
{\displaystyle a\cos x+b\sin x=c\cos(x+\varphi )}
where
c
{\displaystyle c}
φ
{\displaystyle \varphi }
c
=
sgn
(
a
)
a
2
+
b
2
,
φ
=
arctan
(
−
b
/
a
)
,
{\displaystyle {\begin{aligned}c&=\operatorname {sgn}(a){\sqrt {a^{2}+b^{2}}},\\\varphi &={\arctan }{\bigl (}{-b/a}{\bigr )},\end{aligned}}}
given that
a
≠
0.
{\displaystyle a\neq 0.}
Arbitrary phase shift
More generally, for arbitrary phase shifts, we have
a
sin
(
x
+
θ
a
)
+
b
sin
(
x
+
θ
b
)
=
c
sin
(
x
+
φ
)
{\displaystyle a\sin(x+\theta _{a})+b\sin(x+\theta _{b})=c\sin(x+\varphi )}
where
c
{\displaystyle c}
φ
{\displaystyle \varphi }
c
2
=
a
2
+
b
2
+
2
a
b
cos
(
θ
a
−
θ
b
)
,
tan
φ
=
a
sin
θ
a
+
b
sin
θ
b
a
cos
θ
a
+
b
cos
θ
b
.
{\displaystyle {\begin{aligned}c^{2}&=a^{2}+b^{2}+2ab\cos \left(\theta _{a}-\theta _{b}\right),\\\tan \varphi &={\frac {a\sin \theta _{a}+b\sin \theta _{b}}{a\cos \theta _{a}+b\cos \theta _{b}}}.\end{aligned}}}
More than two sinusoids
The general case reads[ 36]
∑
i
a
i
sin
(
x
+
θ
i
)
=
a
sin
(
x
+
θ
)
,
{\displaystyle \sum _{i}a_{i}\sin(x+\theta _{i})=a\sin(x+\theta ),}
a
2
=
∑
i
,
j
a
i
a
j
cos
(
θ
i
−
θ
j
)
{\displaystyle a^{2}=\sum _{i,j}a_{i}a_{j}\cos(\theta _{i}-\theta _{j})}
tan
θ
=
∑
i
a
i
sin
θ
i
∑
i
a
i
cos
θ
i
.
{\displaystyle \tan \theta ={\frac {\sum _{i}a_{i}\sin \theta _{i}}{\sum _{i}a_{i}\cos \theta _{i}}}.}
These identities, named after Joseph Louis Lagrange , are:[ 37] [ 38] [ 39]
∑
k
=
0
n
sin
k
θ
=
cos
1
2
θ
−
cos
(
(
n
+
1
2
)
θ
)
2
sin
1
2
θ
∑
k
=
1
n
cos
k
θ
=
−
sin
1
2
θ
+
sin
(
(
n
+
1
2
)
θ
)
2
sin
1
2
θ
{\displaystyle {\begin{aligned}\sum _{k=0}^{n}\sin k\theta &={\frac {\cos {\tfrac {1}{2}}\theta -\cos \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{2\sin {\tfrac {1}{2}}\theta }}\\[5pt]\sum _{k=1}^{n}\cos k\theta &={\frac {-\sin {\tfrac {1}{2}}\theta +\sin \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{2\sin {\tfrac {1}{2}}\theta }}\end{aligned}}}
θ
≢
0
(
mod
2
π
)
.
{\displaystyle \theta \not \equiv 0{\pmod {2\pi }}.}
A related function is the Dirichlet kernel :
D
n
(
θ
)
=
1
+
2
∑
k
=
1
n
cos
k
θ
=
sin
(
(
n
+
1
2
)
θ
)
sin
1
2
θ
.
{\displaystyle D_{n}(\theta )=1+2\sum _{k=1}^{n}\cos k\theta ={\frac {\sin \left(\left(n+{\tfrac {1}{2}}\right)\theta \right)}{\sin {\tfrac {1}{2}}\theta }}.}
A similar identity is[ 40]
∑
k
=
1
n
cos
(
2
k
−
1
)
α
=
sin
(
2
n
α
)
2
sin
α
.
{\displaystyle \sum _{k=1}^{n}\cos(2k-1)\alpha ={\frac {\sin(2n\alpha )}{2\sin \alpha }}.}
The proof is the following. By using the angle sum and difference identities ,
sin
(
A
+
B
)
−
sin
(
A
−
B
)
=
2
cos
A
sin
B
.
{\displaystyle \sin(A+B)-\sin(A-B)=2\cos A\sin B.}
2
sin
α
∑
k
=
1
n
cos
(
2
k
−
1
)
α
=
2
sin
α
cos
α
+
2
sin
α
cos
3
α
+
2
sin
α
cos
5
α
+
⋯
+
2
sin
α
cos
(
2
n
−
1
)
α
{\displaystyle 2\sin \alpha \sum _{k=1}^{n}\cos(2k-1)\alpha =2\sin \alpha \cos \alpha +2\sin \alpha \cos 3\alpha +2\sin \alpha \cos 5\alpha +\cdots +2\sin \alpha \cos(2n-1)\alpha }
2
sin
α
∑
k
=
1
n
cos
(
2
k
−
1
)
α
=
∑
k
=
1
n
(
sin
(
2
k
α
)
−
sin
(
2
(
k
−
1
)
α
)
)
=
(
sin
2
α
−
sin
0
)
+
(
sin
4
α
−
sin
2
α
)
+
(
sin
6
α
−
sin
4
α
)
+
⋯
+
(
sin
(
2
n
α
)
−
sin
(
2
(
n
−
1
)
α
)
)
=
sin
(
2
n
α
)
.
{\displaystyle {\begin{aligned}&2\sin \alpha \sum _{k=1}^{n}\cos(2k-1)\alpha \\&\quad =\sum _{k=1}^{n}(\sin(2k\alpha )-\sin(2(k-1)\alpha ))\\&\quad =(\sin 2\alpha -\sin 0)+(\sin 4\alpha -\sin 2\alpha )+(\sin 6\alpha -\sin 4\alpha )+\cdots +(\sin(2n\alpha )-\sin(2(n-1)\alpha ))\\&\quad =\sin(2n\alpha ).\end{aligned}}}
So, dividing this formula with
2
sin
α
{\displaystyle 2\sin \alpha }
If
f
(
x
)
{\displaystyle f(x)}
linear fractional transformation
f
(
x
)
=
(
cos
α
)
x
−
sin
α
(
sin
α
)
x
+
cos
α
,
{\displaystyle f(x)={\frac {(\cos \alpha )x-\sin \alpha }{(\sin \alpha )x+\cos \alpha }},}
g
(
x
)
=
(
cos
β
)
x
−
sin
β
(
sin
β
)
x
+
cos
β
,
{\displaystyle g(x)={\frac {(\cos \beta )x-\sin \beta }{(\sin \beta )x+\cos \beta }},}
f
(
g
(
x
)
)
=
g
(
f
(
x
)
)
=
(
cos
(
α
+
β
)
)
x
−
sin
(
α
+
β
)
(
sin
(
α
+
β
)
)
x
+
cos
(
α
+
β
)
.
{\displaystyle f{\big (}g(x){\big )}=g{\big (}f(x){\big )}={\frac {{\big (}\cos(\alpha +\beta ){\big )}x-\sin(\alpha +\beta )}{{\big (}\sin(\alpha +\beta ){\big )}x+\cos(\alpha +\beta )}}.}
More tersely stated, if for all
α
{\displaystyle \alpha }
f
α
{\displaystyle f_{\alpha }}
f
{\displaystyle f}
f
α
∘
f
β
=
f
α
+
β
.
{\displaystyle f_{\alpha }\circ f_{\beta }=f_{\alpha +\beta }.}
If
x
{\displaystyle x}
f
(
x
)
{\displaystyle f(x)}
−
α
.
{\displaystyle -\alpha .}
Relation to the complex exponential function
Euler's formula states that, for any real number x :[ 41]
e
i
x
=
cos
x
+
i
sin
x
,
{\displaystyle e^{ix}=\cos x+i\sin x,}
i is the imaginary unit . Substituting −x for x gives us:
e
−
i
x
=
cos
(
−
x
)
+
i
sin
(
−
x
)
=
cos
x
−
i
sin
x
.
{\displaystyle e^{-ix}=\cos(-x)+i\sin(-x)=\cos x-i\sin x.}
These two equations can be used to solve for cosine and sine in terms of the exponential function . Specifically,[ 42] [ 43]
cos
x
=
e
i
x
+
e
−
i
x
2
{\displaystyle \cos x={\frac {e^{ix}+e^{-ix}}{2}}}
sin
x
=
e
i
x
−
e
−
i
x
2
i
{\displaystyle \sin x={\frac {e^{ix}-e^{-ix}}{2i}}}
These formulae are useful for proving many other trigonometric identities. For example, that
e i (θ +φ )e iθ e iφ
cos(θ + φ ) + i sin(θ + φ ) = (cos θ + i sin θ ) (cos φ + i sin φ ) = (cos θ cos φ − sin θ sin φ ) + i (cos θ sin φ + sin θ cos φ ) .
That the real part of the left hand side equals the real part of the right hand side is an angle addition formula for cosine. The equality of the imaginary parts gives an angle addition formula for sine.
The following table expresses the trigonometric functions and their inverses in terms of the exponential function and the complex logarithm .
Function
Inverse function[ 44]
sin
θ
=
e
i
θ
−
e
−
i
θ
2
i
{\displaystyle \sin \theta ={\frac {e^{i\theta }-e^{-i\theta }}{2i}}}
arcsin
x
=
−
i
ln
(
i
x
+
1
−
x
2
)
{\displaystyle \arcsin x=-i\,\ln \left(ix+{\sqrt {1-x^{2}}}\right)}
cos
θ
=
e
i
θ
+
e
−
i
θ
2
{\displaystyle \cos \theta ={\frac {e^{i\theta }+e^{-i\theta }}{2}}}
arccos
x
=
−
i
ln
(
x
+
x
2
−
1
)
{\displaystyle \arccos x=-i\ln \left(x+{\sqrt {x^{2}-1}}\right)}
tan
θ
=
−
i
e
i
θ
−
e
−
i
θ
e
i
θ
+
e
−
i
θ
{\displaystyle \tan \theta =-i\,{\frac {e^{i\theta }-e^{-i\theta }}{e^{i\theta }+e^{-i\theta }}}}
arctan
x
=
i
2
ln
(
i
+
x
i
−
x
)
{\displaystyle \arctan x={\frac {i}{2}}\ln \left({\frac {i+x}{i-x}}\right)}
csc
θ
=
2
i
e
i
θ
−
e
−
i
θ
{\displaystyle \csc \theta ={\frac {2i}{e^{i\theta }-e^{-i\theta }}}}
arccsc
x
=
−
i
ln
(
i
x
+
1
−
1
x
2
)
{\displaystyle \operatorname {arccsc} x=-i\,\ln \left({\frac {i}{x}}+{\sqrt {1-{\frac {1}{x^{2}}}}}\right)}
sec
θ
=
2
e
i
θ
+
e
−
i
θ
{\displaystyle \sec \theta ={\frac {2}{e^{i\theta }+e^{-i\theta }}}}
arcsec
x
=
−
i
ln
(
1
x
+
i
1
−
1
x
2
)
{\displaystyle \operatorname {arcsec} x=-i\,\ln \left({\frac {1}{x}}+i{\sqrt {1-{\frac {1}{x^{2}}}}}\right)}
cot
θ
=
i
e
i
θ
+
e
−
i
θ
e
i
θ
−
e
−
i
θ
{\displaystyle \cot \theta =i\,{\frac {e^{i\theta }+e^{-i\theta }}{e^{i\theta }-e^{-i\theta }}}}
arccot
x
=
i
2
ln
(
x
−
i
x
+
i
)
{\displaystyle \operatorname {arccot} x={\frac {i}{2}}\ln \left({\frac {x-i}{x+i}}\right)}
cis
θ
=
e
i
θ
{\displaystyle \operatorname {cis} \theta =e^{i\theta }}
arccis
x
=
−
i
ln
x
{\displaystyle \operatorname {arccis} x=-i\ln x}
Relation to complex hyperbolic functions
Trigonometric functions may be deduced from hyperbolic functions with complex arguments. The formulae for the relations are shown below[ 45] [ 46]
sin
x
=
−
i
sinh
(
i
x
)
cos
x
=
cosh
(
i
x
)
tan
x
=
−
i
tanh
(
i
x
)
cot
x
=
i
coth
(
i
x
)
sec
x
=
sech
(
i
x
)
csc
x
=
i
csch
(
i
x
)
{\displaystyle {\begin{aligned}\sin x&=-i\sinh(ix)\\\cos x&=\cosh(ix)\\\tan x&=-i\tanh(ix)\\\cot x&=i\coth(ix)\\\sec x&=\operatorname {sech} (ix)\\\csc x&=i\operatorname {csch} (ix)\\\end{aligned}}}
Series expansion
When using a power series expansion to define trigonometric functions, the following identities are obtained:[ 47]
sin
x
=
x
−
x
3
3
!
+
x
5
5
!
−
x
7
7
!
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
x
2
n
+
1
(
2
n
+
1
)
!
,
{\displaystyle \sin x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n+1}}{(2n+1)!}},}
cos
x
=
1
−
x
2
2
!
+
x
4
4
!
−
x
6
6
!
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
x
2
n
(
2
n
)
!
.
{\displaystyle \cos x=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}x^{2n}}{(2n)!}}.}
For applications to special functions , the following infinite product formulae for trigonometric functions are useful:[ 48] [ 49]
sin
x
=
x
∏
n
=
1
∞
(
1
−
x
2
π
2
n
2
)
,
cos
x
=
∏
n
=
1
∞
(
1
−
x
2
π
2
(
n
−
1
2
)
)
2
)
,
sinh
x
=
x
∏
n
=
1
∞
(
1
+
x
2
π
2
n
2
)
,
cosh
x
=
∏
n
=
1
∞
(
1
+
x
2
π
2
(
n
−
1
2
)
)
2
)
.
{\displaystyle {\begin{aligned}\sin x&=x\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}n^{2}}}\right),&\cos x&=\prod _{n=1}^{\infty }\left(1-{\frac {x^{2}}{\pi ^{2}\left(n-{\frac {1}{2}}\right)\!{\vphantom {)}}^{2}}}\right),\\[10mu]\sinh x&=x\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}n^{2}}}\right),&\cosh x&=\prod _{n=1}^{\infty }\left(1+{\frac {x^{2}}{\pi ^{2}\left(n-{\frac {1}{2}}\right)\!{\vphantom {)}}^{2}}}\right).\end{aligned}}}
Inverse trigonometric functions
The following identities give the result of composing a trigonometric function with an inverse trigonometric function.[ 50]
sin
(
arcsin
x
)
=
x
cos
(
arcsin
x
)
=
1
−
x
2
tan
(
arcsin
x
)
=
x
1
−
x
2
sin
(
arccos
x
)
=
1
−
x
2
cos
(
arccos
x
)
=
x
tan
(
arccos
x
)
=
1
−
x
2
x
sin
(
arctan
x
)
=
x
1
+
x
2
cos
(
arctan
x
)
=
1
1
+
x
2
tan
(
arctan
x
)
=
x
sin
(
arccsc
x
)
=
1
x
cos
(
arccsc
x
)
=
x
2
−
1
x
tan
(
arccsc
x
)
=
1
x
2
−
1
sin
(
arcsec
x
)
=
x
2
−
1
x
cos
(
arcsec
x
)
=
1
x
tan
(
arcsec
x
)
=
x
2
−
1
sin
(
arccot
x
)
=
1
1
+
x
2
cos
(
arccot
x
)
=
x
1
+
x
2
tan
(
arccot
x
)
=
1
x
{\displaystyle {\begin{aligned}\sin(\arcsin x)&=x&\cos(\arcsin x)&={\sqrt {1-x^{2}}}&\tan(\arcsin x)&={\frac {x}{\sqrt {1-x^{2}}}}\\\sin(\arccos x)&={\sqrt {1-x^{2}}}&\cos(\arccos x)&=x&\tan(\arccos x)&={\frac {\sqrt {1-x^{2}}}{x}}\\\sin(\arctan x)&={\frac {x}{\sqrt {1+x^{2}}}}&\cos(\arctan x)&={\frac {1}{\sqrt {1+x^{2}}}}&\tan(\arctan x)&=x\\\sin(\operatorname {arccsc} x)&={\frac {1}{x}}&\cos(\operatorname {arccsc} x)&={\frac {\sqrt {x^{2}-1}}{x}}&\tan(\operatorname {arccsc} x)&={\frac {1}{\sqrt {x^{2}-1}}}\\\sin(\operatorname {arcsec} x)&={\frac {\sqrt {x^{2}-1}}{x}}&\cos(\operatorname {arcsec} x)&={\frac {1}{x}}&\tan(\operatorname {arcsec} x)&={\sqrt {x^{2}-1}}\\\sin(\operatorname {arccot} x)&={\frac {1}{\sqrt {1+x^{2}}}}&\cos(\operatorname {arccot} x)&={\frac {x}{\sqrt {1+x^{2}}}}&\tan(\operatorname {arccot} x)&={\frac {1}{x}}\\\end{aligned}}}
Taking the multiplicative inverse of both sides of the each equation above results in the equations for
csc
=
1
sin
,
sec
=
1
cos
,
and
cot
=
1
tan
.
{\displaystyle \csc ={\frac {1}{\sin }},\;\sec ={\frac {1}{\cos }},{\text{ and }}\cot ={\frac {1}{\tan }}.}
cot
(
arcsin
x
)
{\displaystyle \cot(\arcsin x)}
cot
(
arcsin
x
)
=
1
tan
(
arcsin
x
)
=
1
x
1
−
x
2
=
1
−
x
2
x
{\displaystyle \cot(\arcsin x)={\frac {1}{\tan(\arcsin x)}}={\frac {1}{\frac {x}{\sqrt {1-x^{2}}}}}={\frac {\sqrt {1-x^{2}}}{x}}}
csc
(
arccos
x
)
{\displaystyle \csc(\arccos x)}
sec
(
arccos
x
)
{\displaystyle \sec(\arccos x)}
csc
(
arccos
x
)
=
1
sin
(
arccos
x
)
=
1
1
−
x
2
and
sec
(
arccos
x
)
=
1
cos
(
arccos
x
)
=
1
x
.
{\displaystyle \csc(\arccos x)={\frac {1}{\sin(\arccos x)}}={\frac {1}{\sqrt {1-x^{2}}}}\qquad {\text{ and }}\quad \sec(\arccos x)={\frac {1}{\cos(\arccos x)}}={\frac {1}{x}}.}
The following identities are implied by the reflection identities . They hold whenever
x
,
r
,
s
,
−
x
,
−
r
,
{\displaystyle x,r,s,-x,-r,}
−
s
{\displaystyle -s}
π
2
=
arcsin
(
x
)
+
arccos
(
x
)
=
arctan
(
r
)
+
arccot
(
r
)
=
arcsec
(
s
)
+
arccsc
(
s
)
π
=
arccos
(
x
)
+
arccos
(
−
x
)
=
arccot
(
r
)
+
arccot
(
−
r
)
=
arcsec
(
s
)
+
arcsec
(
−
s
)
0
=
arcsin
(
x
)
+
arcsin
(
−
x
)
=
arctan
(
r
)
+
arctan
(
−
r
)
=
arccsc
(
s
)
+
arccsc
(
−
s
)
{\displaystyle {\begin{alignedat}{9}{\frac {\pi }{2}}~&=~\arcsin(x)&&+\arccos(x)~&&=~\arctan(r)&&+\operatorname {arccot}(r)~&&=~\operatorname {arcsec}(s)&&+\operatorname {arccsc}(s)\\[0.4ex]\pi ~&=~\arccos(x)&&+\arccos(-x)~&&=~\operatorname {arccot}(r)&&+\operatorname {arccot}(-r)~&&=~\operatorname {arcsec}(s)&&+\operatorname {arcsec}(-s)\\[0.4ex]0~&=~\arcsin(x)&&+\arcsin(-x)~&&=~\arctan(r)&&+\arctan(-r)~&&=~\operatorname {arccsc}(s)&&+\operatorname {arccsc}(-s)\\[1.0ex]\end{alignedat}}}
Also,[ 51]
arctan
x
+
arctan
1
x
=
{
π
2
,
if
x
>
0
−
π
2
,
if
x
<
0
arccot
x
+
arccot
1
x
=
{
π
2
,
if
x
>
0
3
π
2
,
if
x
<
0
{\displaystyle {\begin{aligned}\arctan x+\arctan {\dfrac {1}{x}}&={\begin{cases}{\frac {\pi }{2}},&{\text{if }}x>0\\-{\frac {\pi }{2}},&{\text{if }}x<0\end{cases}}\\\operatorname {arccot} x+\operatorname {arccot} {\dfrac {1}{x}}&={\begin{cases}{\frac {\pi }{2}},&{\text{if }}x>0\\{\frac {3\pi }{2}},&{\text{if }}x<0\end{cases}}\\\end{aligned}}}
arccos
1
x
=
arcsec
x
and
arcsec
1
x
=
arccos
x
{\displaystyle \arccos {\frac {1}{x}}=\operatorname {arcsec} x\qquad {\text{ and }}\qquad \operatorname {arcsec} {\frac {1}{x}}=\arccos x}
arcsin
1
x
=
arccsc
x
and
arccsc
1
x
=
arcsin
x
{\displaystyle \arcsin {\frac {1}{x}}=\operatorname {arccsc} x\qquad {\text{ and }}\qquad \operatorname {arccsc} {\frac {1}{x}}=\arcsin x}
The arctangent function can be expanded as a series:[ 52]
arctan
(
n
x
)
=
∑
m
=
1
n
arctan
x
1
+
(
m
−
1
)
m
x
2
{\displaystyle \arctan(nx)=\sum _{m=1}^{n}\arctan {\frac {x}{1+(m-1)mx^{2}}}}
Identities without variables
In terms of the arctangent function we have[ 51]
arctan
1
2
=
arctan
1
3
+
arctan
1
7
.
{\displaystyle \arctan {\frac {1}{2}}=\arctan {\frac {1}{3}}+\arctan {\frac {1}{7}}.}
The curious identity known as Morrie's law ,
cos
20
∘
⋅
cos
40
∘
⋅
cos
80
∘
=
1
8
,
{\displaystyle \cos 20^{\circ }\cdot \cos 40^{\circ }\cdot \cos 80^{\circ }={\frac {1}{8}},}
is a special case of an identity that contains one variable:
∏
j
=
0
k
−
1
cos
(
2
j
x
)
=
sin
(
2
k
x
)
2
k
sin
x
.
{\displaystyle \prod _{j=0}^{k-1}\cos \left(2^{j}x\right)={\frac {\sin \left(2^{k}x\right)}{2^{k}\sin x}}.}
Similarly,
sin
20
∘
⋅
sin
40
∘
⋅
sin
80
∘
=
3
8
{\displaystyle \sin 20^{\circ }\cdot \sin 40^{\circ }\cdot \sin 80^{\circ }={\frac {\sqrt {3}}{8}}}
x
=
20
∘
{\displaystyle x=20^{\circ }}
sin
x
⋅
sin
(
60
∘
−
x
)
⋅
sin
(
60
∘
+
x
)
=
sin
3
x
4
.
{\displaystyle \sin x\cdot \sin \left(60^{\circ }-x\right)\cdot \sin \left(60^{\circ }+x\right)={\frac {\sin 3x}{4}}.}
For the case
x
=
15
∘
{\displaystyle x=15^{\circ }}
sin
15
∘
⋅
sin
45
∘
⋅
sin
75
∘
=
2
8
,
sin
15
∘
⋅
sin
75
∘
=
1
4
.
{\displaystyle {\begin{aligned}\sin 15^{\circ }\cdot \sin 45^{\circ }\cdot \sin 75^{\circ }&={\frac {\sqrt {2}}{8}},\\\sin 15^{\circ }\cdot \sin 75^{\circ }&={\frac {1}{4}}.\end{aligned}}}
For the case
x
=
10
∘
{\displaystyle x=10^{\circ }}
sin
10
∘
⋅
sin
50
∘
⋅
sin
70
∘
=
1
8
.
{\displaystyle \sin 10^{\circ }\cdot \sin 50^{\circ }\cdot \sin 70^{\circ }={\frac {1}{8}}.}
The same cosine identity is
cos
x
⋅
cos
(
60
∘
−
x
)
⋅
cos
(
60
∘
+
x
)
=
cos
3
x
4
.
{\displaystyle \cos x\cdot \cos \left(60^{\circ }-x\right)\cdot \cos \left(60^{\circ }+x\right)={\frac {\cos 3x}{4}}.}
Similarly,
cos
10
∘
⋅
cos
50
∘
⋅
cos
70
∘
=
3
8
,
cos
15
∘
⋅
cos
45
∘
⋅
cos
75
∘
=
2
8
,
cos
15
∘
⋅
cos
75
∘
=
1
4
.
{\displaystyle {\begin{aligned}\cos 10^{\circ }\cdot \cos 50^{\circ }\cdot \cos 70^{\circ }&={\frac {\sqrt {3}}{8}},\\\cos 15^{\circ }\cdot \cos 45^{\circ }\cdot \cos 75^{\circ }&={\frac {\sqrt {2}}{8}},\\\cos 15^{\circ }\cdot \cos 75^{\circ }&={\frac {1}{4}}.\end{aligned}}}
Similarly,
tan
50
∘
⋅
tan
60
∘
⋅
tan
70
∘
=
tan
80
∘
,
tan
40
∘
⋅
tan
30
∘
⋅
tan
20
∘
=
tan
10
∘
.
{\displaystyle {\begin{aligned}\tan 50^{\circ }\cdot \tan 60^{\circ }\cdot \tan 70^{\circ }&=\tan 80^{\circ },\\\tan 40^{\circ }\cdot \tan 30^{\circ }\cdot \tan 20^{\circ }&=\tan 10^{\circ }.\end{aligned}}}
The following is perhaps not as readily generalized to an identity containing variables (but see explanation below):
cos
24
∘
+
cos
48
∘
+
cos
96
∘
+
cos
168
∘
=
1
2
.
{\displaystyle \cos 24^{\circ }+\cos 48^{\circ }+\cos 96^{\circ }+\cos 168^{\circ }={\frac {1}{2}}.}
Degree measure ceases to be more felicitous than radian measure when we consider this identity with 21 in the denominators:
cos
2
π
21
+
cos
(
2
⋅
2
π
21
)
+
cos
(
4
⋅
2
π
21
)
+
cos
(
5
⋅
2
π
21
)
+
cos
(
8
⋅
2
π
21
)
+
cos
(
10
⋅
2
π
21
)
=
1
2
.
{\displaystyle \cos {\frac {2\pi }{21}}+\cos \left(2\cdot {\frac {2\pi }{21}}\right)+\cos \left(4\cdot {\frac {2\pi }{21}}\right)+\cos \left(5\cdot {\frac {2\pi }{21}}\right)+\cos \left(8\cdot {\frac {2\pi }{21}}\right)+\cos \left(10\cdot {\frac {2\pi }{21}}\right)={\frac {1}{2}}.}
The factors 1, 2, 4, 5, 8, 10 may start to make the pattern clear: they are those integers less than 21 / 2 that are relatively prime to (or have no prime factors in common with) 21. The last several examples are corollaries of a basic fact about the irreducible cyclotomic polynomials : the cosines are the real parts of the zeroes of those polynomials; the sum of the zeroes is the Möbius function evaluated at (in the very last case above) 21; only half of the zeroes are present above. The two identities preceding this last one arise in the same fashion with 21 replaced by 10 and 15, respectively.
Other cosine identities include:[ 53]
2
cos
π
3
=
1
,
2
cos
π
5
×
2
cos
2
π
5
=
1
,
2
cos
π
7
×
2
cos
2
π
7
×
2
cos
3
π
7
=
1
,
{\displaystyle {\begin{aligned}2\cos {\frac {\pi }{3}}&=1,\\2\cos {\frac {\pi }{5}}\times 2\cos {\frac {2\pi }{5}}&=1,\\2\cos {\frac {\pi }{7}}\times 2\cos {\frac {2\pi }{7}}\times 2\cos {\frac {3\pi }{7}}&=1,\end{aligned}}}
cos
π
3
+
cos
π
5
×
cos
2
π
5
+
cos
π
7
×
cos
2
π
7
×
cos
3
π
7
+
⋯
=
1.
{\displaystyle \cos {\frac {\pi }{3}}+\cos {\frac {\pi }{5}}\times \cos {\frac {2\pi }{5}}+\cos {\frac {\pi }{7}}\times \cos {\frac {2\pi }{7}}\times \cos {\frac {3\pi }{7}}+\dots =1.}
Many of those curious identities stem from more general facts like the following:[ 54]
∏
k
=
1
n
−
1
sin
k
π
n
=
n
2
n
−
1
{\displaystyle \prod _{k=1}^{n-1}\sin {\frac {k\pi }{n}}={\frac {n}{2^{n-1}}}}
∏
k
=
1
n
−
1
cos
k
π
n
=
sin
π
n
2
2
n
−
1
.
{\displaystyle \prod _{k=1}^{n-1}\cos {\frac {k\pi }{n}}={\frac {\sin {\frac {\pi n}{2}}}{2^{n-1}}}.}
Combining these gives us
∏
k
=
1
n
−
1
tan
k
π
n
=
n
sin
π
n
2
{\displaystyle \prod _{k=1}^{n-1}\tan {\frac {k\pi }{n}}={\frac {n}{\sin {\frac {\pi n}{2}}}}}
If n is an odd number (
n
=
2
m
+
1
{\displaystyle n=2m+1}
∏
k
=
1
m
tan
k
π
2
m
+
1
=
2
m
+
1
{\displaystyle \prod _{k=1}^{m}\tan {\frac {k\pi }{2m+1}}={\sqrt {2m+1}}}
The transfer function of the Butterworth low pass filter can be expressed in terms of polynomial and poles. By setting the frequency as the cutoff frequency, the following identity can be proved:
∏
k
=
1
n
sin
(
2
k
−
1
)
π
4
n
=
∏
k
=
1
n
cos
(
2
k
−
1
)
π
4
n
=
2
2
n
{\displaystyle \prod _{k=1}^{n}\sin {\frac {\left(2k-1\right)\pi }{4n}}=\prod _{k=1}^{n}\cos {\frac {\left(2k-1\right)\pi }{4n}}={\frac {\sqrt {2}}{2^{n}}}}
π An efficient way to compute π to a large number of digits is based on the following identity without variables, due to Machin . This is known as a Machin-like formula :
π
4
=
4
arctan
1
5
−
arctan
1
239
{\displaystyle {\frac {\pi }{4}}=4\arctan {\frac {1}{5}}-\arctan {\frac {1}{239}}}
Leonhard Euler :
π
4
=
5
arctan
1
7
+
2
arctan
3
79
{\displaystyle {\frac {\pi }{4}}=5\arctan {\frac {1}{7}}+2\arctan {\frac {3}{79}}}
Pythagorean triples :
π
=
arccos
4
5
+
arccos
5
13
+
arccos
16
65
=
arcsin
3
5
+
arcsin
12
13
+
arcsin
63
65
.
{\displaystyle \pi =\arccos {\frac {4}{5}}+\arccos {\frac {5}{13}}+\arccos {\frac {16}{65}}=\arcsin {\frac {3}{5}}+\arcsin {\frac {12}{13}}+\arcsin {\frac {63}{65}}.}
Others include:[ 55] [ 51]
π
4
=
arctan
1
2
+
arctan
1
3
,
{\displaystyle {\frac {\pi }{4}}=\arctan {\frac {1}{2}}+\arctan {\frac {1}{3}},}
π
=
arctan
1
+
arctan
2
+
arctan
3
,
{\displaystyle \pi =\arctan 1+\arctan 2+\arctan 3,}
π
4
=
2
arctan
1
3
+
arctan
1
7
.
{\displaystyle {\frac {\pi }{4}}=2\arctan {\frac {1}{3}}+\arctan {\frac {1}{7}}.}
Generally, for numbers t 1 , ..., t n −1θ n n −1k =1t k π /4, 3π /4)t n π /2 − θ n θ n t 1 , ..., t n −1(−1, 1) . In particular, the computed t n t 1 , ..., t n −1
π
2
=
∑
k
=
1
n
arctan
(
t
k
)
π
=
∑
k
=
1
n
sgn
(
t
k
)
arccos
(
1
−
t
k
2
1
+
t
k
2
)
π
=
∑
k
=
1
n
arcsin
(
2
t
k
1
+
t
k
2
)
π
=
∑
k
=
1
n
arctan
(
2
t
k
1
−
t
k
2
)
,
{\displaystyle {\begin{aligned}{\frac {\pi }{2}}&=\sum _{k=1}^{n}\arctan(t_{k})\\\pi &=\sum _{k=1}^{n}\operatorname {sgn}(t_{k})\arccos \left({\frac {1-t_{k}^{2}}{1+t_{k}^{2}}}\right)\\\pi &=\sum _{k=1}^{n}\arcsin \left({\frac {2t_{k}}{1+t_{k}^{2}}}\right)\\\pi &=\sum _{k=1}^{n}\arctan \left({\frac {2t_{k}}{1-t_{k}^{2}}}\right)\,,\end{aligned}}}
where in all but the first expression, we have used tangent half-angle formulae. The first two formulae work even if one or more of the t k (−1, 1) . Note that if t = p /q (2t , 1 − t 2 , 1 + t 2 ) values in the above formulae are proportional to the Pythagorean triple (2pq , q 2 − p 2 , q 2 + p 2 ) .
For example, for n = 3
π
2
=
arctan
(
a
b
)
+
arctan
(
c
d
)
+
arctan
(
b
d
−
a
c
a
d
+
b
c
)
{\displaystyle {\frac {\pi }{2}}=\arctan \left({\frac {a}{b}}\right)+\arctan \left({\frac {c}{d}}\right)+\arctan \left({\frac {bd-ac}{ad+bc}}\right)}
a , b , c , d > 0
An identity of Euclid
Euclid showed in Book XIII, Proposition 10 of his Elements
sin
2
18
∘
+
sin
2
30
∘
=
sin
2
36
∘
.
{\displaystyle \sin ^{2}18^{\circ }+\sin ^{2}30^{\circ }=\sin ^{2}36^{\circ }.}
Ptolemy used this proposition to compute some angles in his table of chords in Book I, chapter 11 of Almagest
Composition of trigonometric functions
These identities involve a trigonometric function of a trigonometric function:[ 56]
cos
(
t
sin
x
)
=
J
0
(
t
)
+
2
∑
k
=
1
∞
J
2
k
(
t
)
cos
(
2
k
x
)
{\displaystyle \cos(t\sin x)=J_{0}(t)+2\sum _{k=1}^{\infty }J_{2k}(t)\cos(2kx)}
sin
(
t
sin
x
)
=
2
∑
k
=
0
∞
J
2
k
+
1
(
t
)
sin
(
(
2
k
+
1
)
x
)
{\displaystyle \sin(t\sin x)=2\sum _{k=0}^{\infty }J_{2k+1}(t)\sin {\big (}(2k+1)x{\big )}}
cos
(
t
cos
x
)
=
J
0
(
t
)
+
2
∑
k
=
1
∞
(
−
1
)
k
J
2
k
(
t
)
cos
(
2
k
x
)
{\displaystyle \cos(t\cos x)=J_{0}(t)+2\sum _{k=1}^{\infty }(-1)^{k}J_{2k}(t)\cos(2kx)}
sin
(
t
cos
x
)
=
2
∑
k
=
0
∞
(
−
1
)
k
J
2
k
+
1
(
t
)
cos
(
(
2
k
+
1
)
x
)
{\displaystyle \sin(t\cos x)=2\sum _{k=0}^{\infty }(-1)^{k}J_{2k+1}(t)\cos {\big (}(2k+1)x{\big )}}
where Ji are Bessel functions .
α + β + γ = 180°A conditional trigonometric identity is a trigonometric identity that holds if specified conditions on the arguments to the trigonometric functions are satisfied.[ 57]
α
+
β
+
γ
=
180
∘
,
{\displaystyle \alpha +\beta +\gamma =180^{\circ },}
[ 58]
tan
α
+
tan
β
+
tan
γ
=
tan
α
tan
β
tan
γ
1
=
cot
β
cot
γ
+
cot
γ
cot
α
+
cot
α
cot
β
cot
(
α
2
)
+
cot
(
β
2
)
+
cot
(
γ
2
)
=
cot
(
α
2
)
cot
(
β
2
)
cot
(
γ
2
)
1
=
tan
(
β
2
)
tan
(
γ
2
)
+
tan
(
γ
2
)
tan
(
α
2
)
+
tan
(
α
2
)
tan
(
β
2
)
sin
α
+
sin
β
+
sin
γ
=
4
cos
(
α
2
)
cos
(
β
2
)
cos
(
γ
2
)
−
sin
α
+
sin
β
+
sin
γ
=
4
cos
(
α
2
)
sin
(
β
2
)
sin
(
γ
2
)
cos
α
+
cos
β
+
cos
γ
=
4
sin
(
α
2
)
sin
(
β
2
)
sin
(
γ
2
)
+
1
−
cos
α
+
cos
β
+
cos
γ
=
4
sin
(
α
2
)
cos
(
β
2
)
cos
(
γ
2
)
−
1
sin
(
2
α
)
+
sin
(
2
β
)
+
sin
(
2
γ
)
=
4
sin
α
sin
β
sin
γ
−
sin
(
2
α
)
+
sin
(
2
β
)
+
sin
(
2
γ
)
=
4
sin
α
cos
β
cos
γ
cos
(
2
α
)
+
cos
(
2
β
)
+
cos
(
2
γ
)
=
−
4
cos
α
cos
β
cos
γ
−
1
−
cos
(
2
α
)
+
cos
(
2
β
)
+
cos
(
2
γ
)
=
−
4
cos
α
sin
β
sin
γ
+
1
sin
2
α
+
sin
2
β
+
sin
2
γ
=
2
cos
α
cos
β
cos
γ
+
2
−
sin
2
α
+
sin
2
β
+
sin
2
γ
=
2
cos
α
sin
β
sin
γ
cos
2
α
+
cos
2
β
+
cos
2
γ
=
−
2
cos
α
cos
β
cos
γ
+
1
−
cos
2
α
+
cos
2
β
+
cos
2
γ
=
−
2
cos
α
sin
β
sin
γ
+
1
sin
2
(
2
α
)
+
sin
2
(
2
β
)
+
sin
2
(
2
γ
)
=
−
2
cos
(
2
α
)
cos
(
2
β
)
cos
(
2
γ
)
+
2
cos
2
(
2
α
)
+
cos
2
(
2
β
)
+
cos
2
(
2
γ
)
=
2
cos
(
2
α
)
cos
(
2
β
)
cos
(
2
γ
)
+
1
1
=
sin
2
(
α
2
)
+
sin
2
(
β
2
)
+
sin
2
(
γ
2
)
+
2
sin
(
α
2
)
sin
(
β
2
)
sin
(
γ
2
)
{\displaystyle {\begin{aligned}\tan \alpha +\tan \beta +\tan \gamma &=\tan \alpha \tan \beta \tan \gamma \\1&=\cot \beta \cot \gamma +\cot \gamma \cot \alpha +\cot \alpha \cot \beta \\\cot \left({\frac {\alpha }{2}}\right)+\cot \left({\frac {\beta }{2}}\right)+\cot \left({\frac {\gamma }{2}}\right)&=\cot \left({\frac {\alpha }{2}}\right)\cot \left({\frac {\beta }{2}}\right)\cot \left({\frac {\gamma }{2}}\right)\\1&=\tan \left({\frac {\beta }{2}}\right)\tan \left({\frac {\gamma }{2}}\right)+\tan \left({\frac {\gamma }{2}}\right)\tan \left({\frac {\alpha }{2}}\right)+\tan \left({\frac {\alpha }{2}}\right)\tan \left({\frac {\beta }{2}}\right)\\\sin \alpha +\sin \beta +\sin \gamma &=4\cos \left({\frac {\alpha }{2}}\right)\cos \left({\frac {\beta }{2}}\right)\cos \left({\frac {\gamma }{2}}\right)\\-\sin \alpha +\sin \beta +\sin \gamma &=4\cos \left({\frac {\alpha }{2}}\right)\sin \left({\frac {\beta }{2}}\right)\sin \left({\frac {\gamma }{2}}\right)\\\cos \alpha +\cos \beta +\cos \gamma &=4\sin \left({\frac {\alpha }{2}}\right)\sin \left({\frac {\beta }{2}}\right)\sin \left({\frac {\gamma }{2}}\right)+1\\-\cos \alpha +\cos \beta +\cos \gamma &=4\sin \left({\frac {\alpha }{2}}\right)\cos \left({\frac {\beta }{2}}\right)\cos \left({\frac {\gamma }{2}}\right)-1\\\sin(2\alpha )+\sin(2\beta )+\sin(2\gamma )&=4\sin \alpha \sin \beta \sin \gamma \\-\sin(2\alpha )+\sin(2\beta )+\sin(2\gamma )&=4\sin \alpha \cos \beta \cos \gamma \\\cos(2\alpha )+\cos(2\beta )+\cos(2\gamma )&=-4\cos \alpha \cos \beta \cos \gamma -1\\-\cos(2\alpha )+\cos(2\beta )+\cos(2\gamma )&=-4\cos \alpha \sin \beta \sin \gamma +1\\\sin ^{2}\alpha +\sin ^{2}\beta +\sin ^{2}\gamma &=2\cos \alpha \cos \beta \cos \gamma +2\\-\sin ^{2}\alpha +\sin ^{2}\beta +\sin ^{2}\gamma &=2\cos \alpha \sin \beta \sin \gamma \\\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma &=-2\cos \alpha \cos \beta \cos \gamma +1\\-\cos ^{2}\alpha +\cos ^{2}\beta +\cos ^{2}\gamma &=-2\cos \alpha \sin \beta \sin \gamma +1\\\sin ^{2}(2\alpha )+\sin ^{2}(2\beta )+\sin ^{2}(2\gamma )&=-2\cos(2\alpha )\cos(2\beta )\cos(2\gamma )+2\\\cos ^{2}(2\alpha )+\cos ^{2}(2\beta )+\cos ^{2}(2\gamma )&=2\cos(2\alpha )\,\cos(2\beta )\,\cos(2\gamma )+1\\1&=\sin ^{2}\left({\frac {\alpha }{2}}\right)+\sin ^{2}\left({\frac {\beta }{2}}\right)+\sin ^{2}\left({\frac {\gamma }{2}}\right)+2\sin \left({\frac {\alpha }{2}}\right)\,\sin \left({\frac {\beta }{2}}\right)\,\sin \left({\frac {\gamma }{2}}\right)\end{aligned}}}
Historical shorthands
The versine , coversine , haversine , and exsecant were used in navigation. For example, the haversine formula was used to calculate the distance between two points on a sphere. They are rarely used today.
Miscellaneous
Dirichlet kernel
The Dirichlet kernel Dn (x )
1
+
2
cos
x
+
2
cos
(
2
x
)
+
2
cos
(
3
x
)
+
⋯
+
2
cos
(
n
x
)
=
sin
(
(
n
+
1
2
)
x
)
sin
(
1
2
x
)
.
{\displaystyle 1+2\cos x+2\cos(2x)+2\cos(3x)+\cdots +2\cos(nx)={\frac {\sin \left(\left(n+{\frac {1}{2}}\right)x\right)}{\sin \left({\frac {1}{2}}x\right)}}.}
The convolution of any integrable function of period
2
π
{\displaystyle 2\pi }
n
{\displaystyle n}
measure or generalized function .
Tangent half-angle substitution
If we set
t
=
tan
x
2
,
{\displaystyle t=\tan {\frac {x}{2}},}
[ 59]
sin
x
=
2
t
1
+
t
2
;
cos
x
=
1
−
t
2
1
+
t
2
;
e
i
x
=
1
+
i
t
1
−
i
t
;
d
x
=
2
d
t
1
+
t
2
,
{\displaystyle \sin x={\frac {2t}{1+t^{2}}};\qquad \cos x={\frac {1-t^{2}}{1+t^{2}}};\qquad e^{ix}={\frac {1+it}{1-it}};\qquad dx={\frac {2\,dt}{1+t^{2}}},}
e
i
x
=
cos
x
+
i
sin
x
,
{\displaystyle e^{ix}=\cos x+i\sin x,}
cis x
When this substitution of
t
{\displaystyle t}
tan x / 2 is used in calculus , it follows that
sin
x
{\displaystyle \sin x}
2t / 1 + t 2
cos
x
{\displaystyle \cos x}
1 − t 2 / 1 + t 2 dx is replaced by 2 dt / 1 + t 2
sin
x
{\displaystyle \sin x}
cos
x
{\displaystyle \cos x}
t
{\displaystyle t}
antiderivatives .
cos
θ
2
⋅
cos
θ
4
⋅
cos
θ
8
⋯
=
∏
n
=
1
∞
cos
θ
2
n
=
sin
θ
θ
=
sinc
θ
.
{\displaystyle \cos {\frac {\theta }{2}}\cdot \cos {\frac {\theta }{4}}\cdot \cos {\frac {\theta }{8}}\cdots =\prod _{n=1}^{\infty }\cos {\frac {\theta }{2^{n}}}={\frac {\sin \theta }{\theta }}=\operatorname {sinc} \theta .}
See also
References
^ Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [June 1964]. "Chapter 4, eqn 4.3.45" . Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables ISBN 978-0-486-61272-0 . LCCN 64-60036 . MR 0167642 . LCCN 65-12253 .^ Selby 1970 , p. 188^ Abramowitz and Stegun, p. 72, 4.3.13–15
^ Abramowitz and Stegun, p. 72, 4.3.7–9
^ Abramowitz and Stegun, p. 72, 4.3.16
^ a b c d Weisstein, Eric W. "Trigonometric Addition Formulas" . MathWorld ^ Abramowitz and Stegun, p. 72, 4.3.17
^ Abramowitz and Stegun, p. 72, 4.3.18
^ a b "Angle Sum and Difference Identities" . www.milefoot.com . Retrieved 2019-10-12 .^ Abramowitz and Stegun, p. 72, 4.3.19
^ Abramowitz and Stegun, p. 80, 4.4.32
^ Abramowitz and Stegun, p. 80, 4.4.33
^ Abramowitz and Stegun, p. 80, 4.4.34
^ Bronstein, Manuel (1989). "Simplification of real elementary functions". In Gonnet, G. H. (ed.). Proceedings of the ACM-SIGSAM 1989 International Symposium on Symbolic and Algebraic Computation . ISSAC '89 (Portland US-OR, 1989-07). New York: ACM . pp. 207– 211. doi :10.1145/74540.74566 . ISBN 0-89791-325-6 . ^ Michael Hardy. (2016). "On Tangents and Secants of Infinite Sums." The American Mathematical Monthly , volume 123, number 7, 701–703. https://doi.org/10.4169/amer.math.monthly.123.7.701
^ Michael Hardy (2025), "Invariance of the Cauchy Family Under Linear Fractional Transformations ," The American Mathematical Monthly , 132:5, 453–455, DOI: 10.1080/00029890.2025.2459048
^ Knight F. B., "A characterization of the Cauchy type." Proceedings of the American Mathematical Society , 1976:130–135.
^ Hardy, Michael (2016). "On Tangents and Secants of Infinite Sums" . American Mathematical Monthly . 123 (7): 701– 703. doi :10.4169/amer.math.monthly.123.7.701 . ^ a b "Sine, Cosine, and Ptolemy's Theorem" .^ a b Weisstein, Eric W. "Multiple-Angle Formulas" . MathWorld ^ Abramowitz and Stegun, p. 74, 4.3.48
^ a b Selby 1970 , pg. 190^ Weisstein, Eric W. "Multiple-Angle Formulas" . mathworld.wolfram.com . Retrieved 2022-02-06 . ^ Ward, Ken. "Multiple angles recursive formula" . Ken Ward's Mathematics Pages . ^ a b Abramowitz, Milton ; Stegun, Irene Ann , eds. (1983) [June 1964]. "Chapter 4, eqn 4.3.20-22" . Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables ISBN 978-0-486-61272-0 . LCCN 64-60036 . MR 0167642 . LCCN 65-12253 .^ a b Weisstein, Eric W. "Half-Angle Formulas" . MathWorld ^ Abramowitz and Stegun, p. 72, 4.3.24–26
^ Weisstein, Eric W. "Double-Angle Formulas" . MathWorld ^ Abramowitz and Stegun, p. 72, 4.3.27–28
^ Abramowitz and Stegun, p. 72, 4.3.31–33
^ Eves, Howard (1990). An introduction to the history of mathematics (6th ed.). Philadelphia: Saunders College Pub. p. 309. ISBN 0-03-029558-0 . OCLC 20842510 . ^ a b Abramowitz and Stegun, p. 72, 4.3.34–39
^ Johnson, Warren P. (Apr 2010). "Trigonometric Identities à la Hermite". American Mathematical Monthly 117 (4): 311– 327. doi :10.4169/000298910x480784 . S2CID 29690311 . ^ "Product Identity Multiple Angle" .^ Apostol, T.M. (1967) Calculus. 2nd edition. New York, NY, Wiley. Pp 334-335.
^ a b Weisstein, Eric W. "Harmonic Addition Theorem" . MathWorld ^ Ortiz Muñiz, Eddie (Feb 1953). "A Method for Deriving Various Formulas in Electrostatics and Electromagnetism Using Lagrange's Trigonometric Identities". American Journal of Physics . 21 (2): 140. Bibcode :1953AmJPh..21..140M . doi :10.1119/1.1933371 . ^ Agarwal, Ravi P.; O'Regan, Donal (2008). Ordinary and Partial Differential Equations: With Special Functions, Fourier Series, and Boundary Value Problems ISBN 978-0-387-79146-3 . Extract of page 185 ^ Jeffrey, Alan; Dai, Hui-hui (2008). "Section 2.4.1.6". Handbook of Mathematical Formulas and Integrals (4th ed.). Academic Press. ISBN 978-0-12-374288-9 . ^ Fay, Temple H.; Kloppers, P. Hendrik (2001). "The Gibbs' phenomenon" International Journal of Mathematical Education in Science and Technology . 32 (1): 73– 89. doi :10.1080/00207390117151 . ^ Abramowitz and Stegun, p. 74, 4.3.47
^ Abramowitz and Stegun, p. 71, 4.3.2
^ Abramowitz and Stegun, p. 71, 4.3.1
^ Abramowitz and Stegun, p. 80, 4.4.26–31
^ Hawkins, Faith Mary; Hawkins, J. Q. (March 1, 1969). Complex Numbers and Elementary Complex Functions ISBN 978-0356025056 . ^ Markushevich, A. I. (1966). The Remarkable Sine Function 35– 37, 81. ISBN 978-1483256313 . ^ Abramowitz and Stegun, p. 74, 4.3.65–66
^ Abramowitz and Stegun, p. 75, 4.3.89–90
^ Abramowitz and Stegun, p. 85, 4.5.68–69
^ Abramowitz & Stegun 1972 , p. 73, 4.3.45^ a b c Wu, Rex H. "Proof Without Words: Euler's Arctangent Identity", Mathematics Magazine 77(3), June 2004, p. 189.
^ S. M. Abrarov; R. K. Jagpal; R. Siddiqui; B. M. Quine (2021), "Algorithmic determination of a large integer in the two-term Machin-like formula for π", Mathematics , 9 (17), 2162, arXiv :2107.01027 doi :10.3390/math9172162 ^ Humble, Steve (Nov 2004). "Grandma's identity". Mathematical Gazette . 88 : 524– 525. doi :10.1017/s0025557200176223 . S2CID 125105552 . ^ Weisstein, Eric W. "Sine" . MathWorld ^ Harris, Edward M. "Sums of Arctangents", in Roger B. Nelson, Proofs Without Words (1993, Mathematical Association of America), p. 39.
^ Milton Abramowitz and Irene Stegun, Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables , Dover Publications , New York, 1972, formulae 9.1.42–9.1.45^ Er. K. C. Joshi, Krishna's IIT MATHEMATIKA . Krishna Prakashan Media. Meerut, India. page 636.
^ Cagnoli, Antonio (1808), Trigonométrie rectiligne et sphérique , p. 27.
^ Abramowitz and Stegun, p. 72, 4.3.23
Bibliography
Abramowitz, Milton ; Stegun, Irene A. , eds. (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables Dover Publications . ISBN 978-0-486-61272-0 .Nielsen, Kaj L. (1966), Logarithmic and Trigonometric Tables to Five Places (2nd ed.), New York: Barnes & Noble , LCCN 61-9103 Selby, Samuel M., ed. (1970), Standard Mathematical Tables (18th ed.), The Chemical Rubber Co.
External links


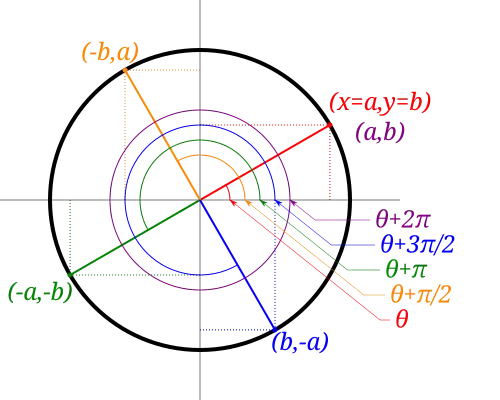

_and_cos(a-b).svg.png)