The derivatives of scalars , vectors , and second-order tensors with respect to second-order tensors are of considerable use in continuum mechanics . These derivatives are used in the theories of nonlinear elasticity and plasticity , particularly in the design of algorithms for numerical simulations .[ 1]
The directional derivative provides a systematic way of finding these derivatives.[ 2]
Derivatives with respect to vectors and second-order tensors
The definitions of directional derivatives for various situations are given below. It is assumed that the functions are sufficiently smooth that derivatives can be taken.
Derivatives of scalar valued functions of vectors
Let f (v ) be a real valued function of the vector v . Then the derivative of f (v ) with respect to v (or at v ) is the vector defined through its dot product with any vector u being
∂
f
∂
v
⋅
u
=
D
f
(
v
)
[
u
]
=
[
d
d
α
f
(
v
+
α
u
)
]
α
=
0
{\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =Df(\mathbf {v} )[\mathbf {u} ]=\left[{\frac {d}{d\alpha }}~f(\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}}
for all vectors u . The above dot product yields a scalar, and if u is a unit vector gives the directional derivative of f at v , in the u direction.
Properties:
If
f
(
v
)
=
f
1
(
v
)
+
f
2
(
v
)
{\displaystyle f(\mathbf {v} )=f_{1}(\mathbf {v} )+f_{2}(\mathbf {v} )}
∂
f
∂
v
⋅
u
=
(
∂
f
1
∂
v
+
∂
f
2
∂
v
)
⋅
u
{\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial f_{1}}{\partial \mathbf {v} }}+{\frac {\partial f_{2}}{\partial \mathbf {v} }}\right)\cdot \mathbf {u} }
If
f
(
v
)
=
f
1
(
v
)
f
2
(
v
)
{\displaystyle f(\mathbf {v} )=f_{1}(\mathbf {v} )~f_{2}(\mathbf {v} )}
∂
f
∂
v
⋅
u
=
(
∂
f
1
∂
v
⋅
u
)
f
2
(
v
)
+
f
1
(
v
)
(
∂
f
2
∂
v
⋅
u
)
{\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial f_{1}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)~f_{2}(\mathbf {v} )+f_{1}(\mathbf {v} )~\left({\frac {\partial f_{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)}
If
f
(
v
)
=
f
1
(
f
2
(
v
)
)
{\displaystyle f(\mathbf {v} )=f_{1}(f_{2}(\mathbf {v} ))}
∂
f
∂
v
⋅
u
=
∂
f
1
∂
f
2
∂
f
2
∂
v
⋅
u
{\displaystyle {\frac {\partial f}{\partial \mathbf {v} }}\cdot \mathbf {u} ={\frac {\partial f_{1}}{\partial f_{2}}}~{\frac {\partial f_{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} }
Derivatives of vector valued functions of vectors
Let f (v ) be a vector valued function of the vector v . Then the derivative of f (v ) with respect to v (or at v ) is the second order tensor defined through its dot product with any vector u being
∂
f
∂
v
⋅
u
=
D
f
(
v
)
[
u
]
=
[
d
d
α
f
(
v
+
α
u
)
]
α
=
0
{\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =D\mathbf {f} (\mathbf {v} )[\mathbf {u} ]=\left[{\frac {d}{d\alpha }}~\mathbf {f} (\mathbf {v} +\alpha ~\mathbf {u} )\right]_{\alpha =0}}
for all vectors u . The above dot product yields a vector, and if u is a unit vector gives the direction derivative of f at v , in the directional u .
Properties:
If
f
(
v
)
=
f
1
(
v
)
+
f
2
(
v
)
{\displaystyle \mathbf {f} (\mathbf {v} )=\mathbf {f} _{1}(\mathbf {v} )+\mathbf {f} _{2}(\mathbf {v} )}
∂
f
∂
v
⋅
u
=
(
∂
f
1
∂
v
+
∂
f
2
∂
v
)
⋅
u
{\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial \mathbf {f} _{1}}{\partial \mathbf {v} }}+{\frac {\partial \mathbf {f} _{2}}{\partial \mathbf {v} }}\right)\cdot \mathbf {u} }
If
f
(
v
)
=
f
1
(
v
)
×
f
2
(
v
)
{\displaystyle \mathbf {f} (\mathbf {v} )=\mathbf {f} _{1}(\mathbf {v} )\times \mathbf {f} _{2}(\mathbf {v} )}
∂
f
∂
v
⋅
u
=
(
∂
f
1
∂
v
⋅
u
)
×
f
2
(
v
)
+
f
1
(
v
)
×
(
∂
f
2
∂
v
⋅
u
)
{\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} =\left({\frac {\partial \mathbf {f} _{1}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)\times \mathbf {f} _{2}(\mathbf {v} )+\mathbf {f} _{1}(\mathbf {v} )\times \left({\frac {\partial \mathbf {f} _{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)}
If
f
(
v
)
=
f
1
(
f
2
(
v
)
)
{\displaystyle \mathbf {f} (\mathbf {v} )=\mathbf {f} _{1}(\mathbf {f} _{2}(\mathbf {v} ))}
∂
f
∂
v
⋅
u
=
∂
f
1
∂
f
2
⋅
(
∂
f
2
∂
v
⋅
u
)
{\displaystyle {\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}\cdot \mathbf {u} ={\frac {\partial \mathbf {f} _{1}}{\partial \mathbf {f} _{2}}}\cdot \left({\frac {\partial \mathbf {f} _{2}}{\partial \mathbf {v} }}\cdot \mathbf {u} \right)}
Derivatives of scalar valued functions of second-order tensors
Let
f
(
S
)
{\displaystyle f({\boldsymbol {S}})}
S
{\displaystyle {\boldsymbol {S}}}
f
(
S
)
{\displaystyle f({\boldsymbol {S}})}
S
{\displaystyle {\boldsymbol {S}}}
S
{\displaystyle {\boldsymbol {S}}}
T
{\displaystyle {\boldsymbol {T}}}
second order tensor defined as
∂
f
∂
S
:
T
=
D
f
(
S
)
[
T
]
=
[
d
d
α
f
(
S
+
α
T
)
]
α
=
0
{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=Df({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {d}{d\alpha }}~f({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}}
T
{\displaystyle {\boldsymbol {T}}}
Properties:
If
f
(
S
)
=
f
1
(
S
)
+
f
2
(
S
)
{\displaystyle f({\boldsymbol {S}})=f_{1}({\boldsymbol {S}})+f_{2}({\boldsymbol {S}})}
∂
f
∂
S
:
T
=
(
∂
f
1
∂
S
+
∂
f
2
∂
S
)
:
T
{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial f_{1}}{\partial {\boldsymbol {S}}}}+{\frac {\partial f_{2}}{\partial {\boldsymbol {S}}}}\right):{\boldsymbol {T}}}
If
f
(
S
)
=
f
1
(
S
)
f
2
(
S
)
{\displaystyle f({\boldsymbol {S}})=f_{1}({\boldsymbol {S}})~f_{2}({\boldsymbol {S}})}
∂
f
∂
S
:
T
=
(
∂
f
1
∂
S
:
T
)
f
2
(
S
)
+
f
1
(
S
)
(
∂
f
2
∂
S
:
T
)
{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial f_{1}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)~f_{2}({\boldsymbol {S}})+f_{1}({\boldsymbol {S}})~\left({\frac {\partial f_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)}
If
f
(
S
)
=
f
1
(
f
2
(
S
)
)
{\displaystyle f({\boldsymbol {S}})=f_{1}(f_{2}({\boldsymbol {S}}))}
∂
f
∂
S
:
T
=
∂
f
1
∂
f
2
(
∂
f
2
∂
S
:
T
)
{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}={\frac {\partial f_{1}}{\partial f_{2}}}~\left({\frac {\partial f_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)}
Derivatives of tensor valued functions of second-order tensors
Let
F
(
S
)
{\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})}
S
{\displaystyle {\boldsymbol {S}}}
F
(
S
)
{\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})}
S
{\displaystyle {\boldsymbol {S}}}
S
{\displaystyle {\boldsymbol {S}}}
T
{\displaystyle {\boldsymbol {T}}}
fourth order tensor defined as
∂
F
∂
S
:
T
=
D
F
(
S
)
[
T
]
=
[
d
d
α
F
(
S
+
α
T
)
]
α
=
0
{\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=D{\boldsymbol {F}}({\boldsymbol {S}})[{\boldsymbol {T}}]=\left[{\frac {d}{d\alpha }}~{\boldsymbol {F}}({\boldsymbol {S}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}}
T
{\displaystyle {\boldsymbol {T}}}
Properties:
If
F
(
S
)
=
F
1
(
S
)
+
F
2
(
S
)
{\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})={\boldsymbol {F}}_{1}({\boldsymbol {S}})+{\boldsymbol {F}}_{2}({\boldsymbol {S}})}
∂
F
∂
S
:
T
=
(
∂
F
1
∂
S
+
∂
F
2
∂
S
)
:
T
{\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}+{\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}\right):{\boldsymbol {T}}}
If
F
(
S
)
=
F
1
(
S
)
⋅
F
2
(
S
)
{\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})={\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot {\boldsymbol {F}}_{2}({\boldsymbol {S}})}
∂
F
∂
S
:
T
=
(
∂
F
1
∂
S
:
T
)
⋅
F
2
(
S
)
+
F
1
(
S
)
⋅
(
∂
F
2
∂
S
:
T
)
{\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {F}}_{2}({\boldsymbol {S}})+{\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot \left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)}
If
F
(
S
)
=
F
1
(
F
2
(
S
)
)
{\displaystyle {\boldsymbol {F}}({\boldsymbol {S}})={\boldsymbol {F}}_{1}({\boldsymbol {F}}_{2}({\boldsymbol {S}}))}
∂
F
∂
S
:
T
=
∂
F
1
∂
F
2
:
(
∂
F
2
∂
S
:
T
)
{\displaystyle {\frac {\partial {\boldsymbol {F}}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}={\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {F}}_{2}}}:\left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)}
If
f
(
S
)
=
f
1
(
F
2
(
S
)
)
{\displaystyle f({\boldsymbol {S}})=f_{1}({\boldsymbol {F}}_{2}({\boldsymbol {S}}))}
∂
f
∂
S
:
T
=
∂
f
1
∂
F
2
:
(
∂
F
2
∂
S
:
T
)
{\displaystyle {\frac {\partial f}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}={\frac {\partial f_{1}}{\partial {\boldsymbol {F}}_{2}}}:\left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)}
Gradient of a tensor field
The gradient ,
∇
T
{\displaystyle {\boldsymbol {\nabla }}{\boldsymbol {T}}}
T
(
x
)
{\displaystyle {\boldsymbol {T}}(\mathbf {x} )}
c is defined as:
∇
T
⋅
c
=
lim
α
→
0
d
d
α
T
(
x
+
α
c
)
{\displaystyle {\boldsymbol {\nabla }}{\boldsymbol {T}}\cdot \mathbf {c} =\lim _{\alpha \rightarrow 0}\quad {\cfrac {d}{d\alpha }}~{\boldsymbol {T}}(\mathbf {x} +\alpha \mathbf {c} )}
n is a tensor field of order n +1.
Cartesian coordinates
If
e
1
,
e
2
,
e
3
{\displaystyle \mathbf {e} _{1},\mathbf {e} _{2},\mathbf {e} _{3}}
Cartesian coordinate system, with coordinates of points denoted by (
x
1
,
x
2
,
x
3
{\displaystyle x_{1},x_{2},x_{3}}
T
{\displaystyle {\boldsymbol {T}}}
∇
T
=
∂
T
∂
x
i
⊗
e
i
{\displaystyle {\boldsymbol {\nabla }}{\boldsymbol {T}}={\cfrac {\partial {\boldsymbol {T}}}{\partial x_{i}}}\otimes \mathbf {e} _{i}}
Since the basis vectors do not vary in a Cartesian coordinate system we have the following relations for the gradients of a scalar field
ϕ
{\displaystyle \phi }
v , and a second-order tensor field
S
{\displaystyle {\boldsymbol {S}}}
∇
ϕ
=
∂
ϕ
∂
x
i
e
i
=
ϕ
,
i
e
i
∇
v
=
∂
(
v
j
e
j
)
∂
x
i
⊗
e
i
=
∂
v
j
∂
x
i
e
j
⊗
e
i
=
v
j
,
i
e
j
⊗
e
i
∇
S
=
∂
(
S
j
k
e
j
⊗
e
k
)
∂
x
i
⊗
e
i
=
∂
S
j
k
∂
x
i
e
j
⊗
e
k
⊗
e
i
=
S
j
k
,
i
e
j
⊗
e
k
⊗
e
i
{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\phi &={\cfrac {\partial \phi }{\partial x_{i}}}~\mathbf {e} _{i}=\phi _{,i}~\mathbf {e} _{i}\\{\boldsymbol {\nabla }}\mathbf {v} &={\cfrac {\partial (v_{j}\mathbf {e} _{j})}{\partial x_{i}}}\otimes \mathbf {e} _{i}={\cfrac {\partial v_{j}}{\partial x_{i}}}~\mathbf {e} _{j}\otimes \mathbf {e} _{i}=v_{j,i}~\mathbf {e} _{j}\otimes \mathbf {e} _{i}\\{\boldsymbol {\nabla }}{\boldsymbol {S}}&={\cfrac {\partial (S_{jk}\mathbf {e} _{j}\otimes \mathbf {e} _{k})}{\partial x_{i}}}\otimes \mathbf {e} _{i}={\cfrac {\partial S_{jk}}{\partial x_{i}}}~\mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{i}=S_{jk,i}~\mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{i}\end{aligned}}}
Curvilinear coordinates
If
g
1
,
g
2
,
g
3
{\displaystyle \mathbf {g} ^{1},\mathbf {g} ^{2},\mathbf {g} ^{3}}
contravariant basis vectors in a curvilinear coordinate system, with coordinates of points denoted by (
ξ
1
,
ξ
2
,
ξ
3
{\displaystyle \xi ^{1},\xi ^{2},\xi ^{3}}
T
{\displaystyle {\boldsymbol {T}}}
[ 3]
∇
T
=
∂
T
∂
ξ
i
⊗
g
i
{\displaystyle {\boldsymbol {\nabla }}{\boldsymbol {T}}={\frac {\partial {\boldsymbol {T}}}{\partial \xi ^{i}}}\otimes \mathbf {g} ^{i}}
From this definition we have the following relations for the gradients of a scalar field
ϕ
{\displaystyle \phi }
v , and a second-order tensor field
S
{\displaystyle {\boldsymbol {S}}}
∇
ϕ
=
∂
ϕ
∂
ξ
i
g
i
∇
v
=
∂
(
v
j
g
j
)
∂
ξ
i
⊗
g
i
=
(
∂
v
j
∂
ξ
i
+
v
k
Γ
i
k
j
)
g
j
⊗
g
i
=
(
∂
v
j
∂
ξ
i
−
v
k
Γ
i
j
k
)
g
j
⊗
g
i
∇
S
=
∂
(
S
j
k
g
j
⊗
g
k
)
∂
ξ
i
⊗
g
i
=
(
∂
S
j
k
∂
ξ
i
−
S
l
k
Γ
i
j
l
−
S
j
l
Γ
i
k
l
)
g
j
⊗
g
k
⊗
g
i
{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\phi &={\frac {\partial \phi }{\partial \xi ^{i}}}~\mathbf {g} ^{i}\\[1.2ex]{\boldsymbol {\nabla }}\mathbf {v} &={\frac {\partial \left(v^{j}\mathbf {g} _{j}\right)}{\partial \xi ^{i}}}\otimes \mathbf {g} ^{i}\\&=\left({\frac {\partial v^{j}}{\partial \xi ^{i}}}+v^{k}~\Gamma _{ik}^{j}\right)~\mathbf {g} _{j}\otimes \mathbf {g} ^{i}=\left({\frac {\partial v_{j}}{\partial \xi ^{i}}}-v_{k}~\Gamma _{ij}^{k}\right)~\mathbf {g} ^{j}\otimes \mathbf {g} ^{i}\\[1.2ex]{\boldsymbol {\nabla }}{\boldsymbol {S}}&={\frac {\partial \left(S_{jk}~\mathbf {g} ^{j}\otimes \mathbf {g} ^{k}\right)}{\partial \xi ^{i}}}\otimes \mathbf {g} ^{i}\\&=\left({\frac {\partial S_{jk}}{\partial \xi _{i}}}-S_{lk}~\Gamma _{ij}^{l}-S_{jl}~\Gamma _{ik}^{l}\right)~\mathbf {g} ^{j}\otimes \mathbf {g} ^{k}\otimes \mathbf {g} ^{i}\end{aligned}}}
where the Christoffel symbol
Γ
i
j
k
{\displaystyle \Gamma _{ij}^{k}}
Γ
i
j
k
g
k
=
∂
g
i
∂
ξ
j
⟹
Γ
i
j
k
=
∂
g
i
∂
ξ
j
⋅
g
k
=
−
g
i
⋅
∂
g
k
∂
ξ
j
{\displaystyle \Gamma _{ij}^{k}~\mathbf {g} _{k}={\frac {\partial \mathbf {g} _{i}}{\partial \xi ^{j}}}\quad \implies \quad \Gamma _{ij}^{k}={\frac {\partial \mathbf {g} _{i}}{\partial \xi ^{j}}}\cdot \mathbf {g} ^{k}=-\mathbf {g} _{i}\cdot {\frac {\partial \mathbf {g} ^{k}}{\partial \xi ^{j}}}}
Cylindrical polar coordinates
In cylindrical coordinates , the gradient is given by
∇
ϕ
=
∂
ϕ
∂
r
e
r
+
1
r
∂
ϕ
∂
θ
e
θ
+
∂
ϕ
∂
z
e
z
{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\phi ={}\quad &{\frac {\partial \phi }{\partial r}}~\mathbf {e} _{r}+{\frac {1}{r}}~{\frac {\partial \phi }{\partial \theta }}~\mathbf {e} _{\theta }+{\frac {\partial \phi }{\partial z}}~\mathbf {e} _{z}\\\end{aligned}}}
∇
v
=
∂
v
r
∂
r
e
r
⊗
e
r
+
1
r
(
∂
v
r
∂
θ
−
v
θ
)
e
r
⊗
e
θ
+
∂
v
r
∂
z
e
r
⊗
e
z
+
∂
v
θ
∂
r
e
θ
⊗
e
r
+
1
r
(
∂
v
θ
∂
θ
+
v
r
)
e
θ
⊗
e
θ
+
∂
v
θ
∂
z
e
θ
⊗
e
z
+
∂
v
z
∂
r
e
z
⊗
e
r
+
1
r
∂
v
z
∂
θ
e
z
⊗
e
θ
+
∂
v
z
∂
z
e
z
⊗
e
z
{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\mathbf {v} ={}\quad &{\frac {\partial v_{r}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {1}{r}}\left({\frac {\partial v_{r}}{\partial \theta }}-v_{\theta }\right)~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{r}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\\{}+{}&{\frac {\partial v_{\theta }}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {1}{r}}\left({\frac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{\theta }}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\\{}+{}&{\frac {\partial v_{z}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {1}{r}}{\frac {\partial v_{z}}{\partial \theta }}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }+{\frac {\partial v_{z}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\\\end{aligned}}}
∇
S
=
∂
S
r
r
∂
r
e
r
⊗
e
r
⊗
e
r
+
∂
S
r
r
∂
z
e
r
⊗
e
r
⊗
e
z
+
1
r
[
∂
S
r
r
∂
θ
−
(
S
θ
r
+
S
r
θ
)
]
e
r
⊗
e
r
⊗
e
θ
+
∂
S
r
θ
∂
r
e
r
⊗
e
θ
⊗
e
r
+
∂
S
r
θ
∂
z
e
r
⊗
e
θ
⊗
e
z
+
1
r
[
∂
S
r
θ
∂
θ
+
(
S
r
r
−
S
θ
θ
)
]
e
r
⊗
e
θ
⊗
e
θ
+
∂
S
r
z
∂
r
e
r
⊗
e
z
⊗
e
r
+
∂
S
r
z
∂
z
e
r
⊗
e
z
⊗
e
z
+
1
r
[
∂
S
r
z
∂
θ
−
S
θ
z
]
e
r
⊗
e
z
⊗
e
θ
+
∂
S
θ
r
∂
r
e
θ
⊗
e
r
⊗
e
r
+
∂
S
θ
r
∂
z
e
θ
⊗
e
r
⊗
e
z
+
1
r
[
∂
S
θ
r
∂
θ
+
(
S
r
r
−
S
θ
θ
)
]
e
θ
⊗
e
r
⊗
e
θ
+
∂
S
θ
θ
∂
r
e
θ
⊗
e
θ
⊗
e
r
+
∂
S
θ
θ
∂
z
e
θ
⊗
e
θ
⊗
e
z
+
1
r
[
∂
S
θ
θ
∂
θ
+
(
S
r
θ
+
S
θ
r
)
]
e
θ
⊗
e
θ
⊗
e
θ
+
∂
S
θ
z
∂
r
e
θ
⊗
e
z
⊗
e
r
+
∂
S
θ
z
∂
z
e
θ
⊗
e
z
⊗
e
z
+
1
r
[
∂
S
θ
z
∂
θ
+
S
r
z
]
e
θ
⊗
e
z
⊗
e
θ
+
∂
S
z
r
∂
r
e
z
⊗
e
r
⊗
e
r
+
∂
S
z
r
∂
z
e
z
⊗
e
r
⊗
e
z
+
1
r
[
∂
S
z
r
∂
θ
−
S
z
θ
]
e
z
⊗
e
r
⊗
e
θ
+
∂
S
z
θ
∂
r
e
z
⊗
e
θ
⊗
e
r
+
∂
S
z
θ
∂
z
e
z
⊗
e
θ
⊗
e
z
+
1
r
[
∂
S
z
θ
∂
θ
+
S
z
r
]
e
z
⊗
e
θ
⊗
e
θ
+
∂
S
z
z
∂
r
e
z
⊗
e
z
⊗
e
r
+
∂
S
z
z
∂
z
e
z
⊗
e
z
⊗
e
z
+
1
r
∂
S
z
z
∂
θ
e
z
⊗
e
z
⊗
e
θ
{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}{\boldsymbol {S}}={}\quad &{\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{rr}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{rr}}{\partial \theta }}-(S_{\theta r}+S_{r\theta })\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{r\theta }}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{rz}}{\partial z}}~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{rz}}{\partial \theta }}-S_{\theta z}\right]~\mathbf {e} _{r}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta r}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta r}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta \theta }}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta \theta }}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{\theta z}}{\partial r}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{\theta z}}{\partial z}}~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{\theta }\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{zr}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{zr}}{\partial \theta }}-S_{z\theta }\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{r}\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{z\theta }}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{z}+{\frac {1}{r}}\left[{\frac {\partial S_{z\theta }}{\partial \theta }}+S_{zr}\right]~\mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\otimes \mathbf {e} _{\theta }\\{}+{}&{\frac {\partial S_{zz}}{\partial r}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{r}+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{z}+{\frac {1}{r}}~{\frac {\partial S_{zz}}{\partial \theta }}~\mathbf {e} _{z}\otimes \mathbf {e} _{z}\otimes \mathbf {e} _{\theta }\end{aligned}}}
Divergence of a tensor field
The divergence of a tensor field
T
(
x
)
{\displaystyle {\boldsymbol {T}}(\mathbf {x} )}
(
∇
⋅
T
)
⋅
c
=
∇
⋅
(
c
⋅
T
T
)
;
∇
⋅
v
=
tr
(
∇
v
)
{\displaystyle ({\boldsymbol {\nabla }}\cdot {\boldsymbol {T}})\cdot \mathbf {c} ={\boldsymbol {\nabla }}\cdot \left(\mathbf {c} \cdot {\boldsymbol {T}}^{\textsf {T}}\right)~;\qquad {\boldsymbol {\nabla }}\cdot \mathbf {v} ={\text{tr}}({\boldsymbol {\nabla }}\mathbf {v} )}
where c is an arbitrary constant vector and v is a vector field. If
T
{\displaystyle {\boldsymbol {T}}}
n > 1 then the divergence of the field is a tensor of order n − 1.
Cartesian coordinates
In a Cartesian coordinate system we have the following relations for a vector field v and a second-order tensor field
S
{\displaystyle {\boldsymbol {S}}}
∇
⋅
v
=
∂
v
i
∂
x
i
=
v
i
,
i
∇
⋅
S
=
∂
S
i
k
∂
x
i
e
k
=
S
i
k
,
i
e
k
{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} &={\frac {\partial v_{i}}{\partial x_{i}}}=v_{i,i}\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&={\frac {\partial S_{ik}}{\partial x_{i}}}~\mathbf {e} _{k}=S_{ik,i}~\mathbf {e} _{k}\end{aligned}}}
where tensor index notation for partial derivatives is used in the rightmost expressions. Note that
∇
⋅
S
≠
∇
⋅
S
T
.
{\displaystyle {\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}\neq {\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}^{\textsf {T}}.}
For a symmetric second-order tensor, the divergence is also often written as[ 4]
∇
⋅
S
=
∂
S
k
i
∂
x
i
e
k
=
S
k
i
,
i
e
k
{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&={\cfrac {\partial S_{ki}}{\partial x_{i}}}~\mathbf {e} _{k}=S_{ki,i}~\mathbf {e} _{k}\end{aligned}}}
The above expression is sometimes used as the definition of
∇
⋅
S
{\displaystyle {\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}}
div
S
{\displaystyle \operatorname {div} {\boldsymbol {S}}}
The difference stems from whether the differentiation is performed with respect to the rows or columns of
S
{\displaystyle {\boldsymbol {S}}}
S
{\displaystyle \mathbf {S} }
v
{\displaystyle \mathbf {v} }
∇
⋅
(
∇
v
)
=
∇
⋅
(
v
i
,
j
e
i
⊗
e
j
)
=
v
i
,
j
i
e
i
⋅
e
i
⊗
e
j
=
(
∇
⋅
v
)
,
j
e
j
=
∇
(
∇
⋅
v
)
∇
⋅
[
(
∇
v
)
T
]
=
∇
⋅
(
v
j
,
i
e
i
⊗
e
j
)
=
v
j
,
i
i
e
i
⋅
e
i
⊗
e
j
=
∇
2
v
j
e
j
=
∇
2
v
{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \left({\boldsymbol {\nabla }}\mathbf {v} \right)&={\boldsymbol {\nabla }}\cdot \left(v_{i,j}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{i,ji}~\mathbf {e} _{i}\cdot \mathbf {e} _{i}\otimes \mathbf {e} _{j}=\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)_{,j}~\mathbf {e} _{j}={\boldsymbol {\nabla }}\left({\boldsymbol {\nabla }}\cdot \mathbf {v} \right)\\{\boldsymbol {\nabla }}\cdot \left[\left({\boldsymbol {\nabla }}\mathbf {v} \right)^{\textsf {T}}\right]&={\boldsymbol {\nabla }}\cdot \left(v_{j,i}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{j,ii}~\mathbf {e} _{i}\cdot \mathbf {e} _{i}\otimes \mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}v_{j}~\mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}\mathbf {v} \end{aligned}}}
The last equation is equivalent to the alternative definition / interpretation[ 4]
(
∇
⋅
)
alt
(
∇
v
)
=
(
∇
⋅
)
alt
(
v
i
,
j
e
i
⊗
e
j
)
=
v
i
,
j
j
e
i
⊗
e
j
⋅
e
j
=
∇
2
v
i
e
i
=
∇
2
v
{\displaystyle {\begin{aligned}\left({\boldsymbol {\nabla }}\cdot \right)_{\text{alt}}\left({\boldsymbol {\nabla }}\mathbf {v} \right)=\left({\boldsymbol {\nabla }}\cdot \right)_{\text{alt}}\left(v_{i,j}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\right)=v_{i,jj}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\cdot \mathbf {e} _{j}={\boldsymbol {\nabla }}^{2}v_{i}~\mathbf {e} _{i}={\boldsymbol {\nabla }}^{2}\mathbf {v} \end{aligned}}}
Curvilinear coordinates
In curvilinear coordinates, the divergences of a vector field v and a second-order tensor field
S
{\displaystyle {\boldsymbol {S}}}
∇
⋅
v
=
(
∂
v
i
∂
ξ
i
+
v
k
Γ
i
k
i
)
∇
⋅
S
=
(
∂
S
i
k
∂
ξ
i
−
S
l
k
Γ
i
i
l
−
S
i
l
Γ
i
k
l
)
g
k
{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} &=\left({\cfrac {\partial v^{i}}{\partial \xi ^{i}}}+v^{k}~\Gamma _{ik}^{i}\right)\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&=\left({\cfrac {\partial S_{ik}}{\partial \xi _{i}}}-S_{lk}~\Gamma _{ii}^{l}-S_{il}~\Gamma _{ik}^{l}\right)~\mathbf {g} ^{k}\end{aligned}}}
More generally,
∇
⋅
S
=
[
∂
S
i
j
∂
q
k
−
Γ
k
i
l
S
l
j
−
Γ
k
j
l
S
i
l
]
g
i
k
b
j
=
[
∂
S
i
j
∂
q
i
+
Γ
i
l
i
S
l
j
+
Γ
i
l
j
S
i
l
]
b
j
=
[
∂
S
j
i
∂
q
i
+
Γ
i
l
i
S
j
l
−
Γ
i
j
l
S
l
i
]
b
j
=
[
∂
S
i
j
∂
q
k
−
Γ
i
k
l
S
l
j
+
Γ
k
l
j
S
i
l
]
g
i
k
b
j
{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}&=\left[{\cfrac {\partial S_{ij}}{\partial q^{k}}}-\Gamma _{ki}^{l}~S_{lj}-\Gamma _{kj}^{l}~S_{il}\right]~g^{ik}~\mathbf {b} ^{j}\\[8pt]&=\left[{\cfrac {\partial S^{ij}}{\partial q^{i}}}+\Gamma _{il}^{i}~S^{lj}+\Gamma _{il}^{j}~S^{il}\right]~\mathbf {b} _{j}\\[8pt]&=\left[{\cfrac {\partial S_{~j}^{i}}{\partial q^{i}}}+\Gamma _{il}^{i}~S_{~j}^{l}-\Gamma _{ij}^{l}~S_{~l}^{i}\right]~\mathbf {b} ^{j}\\[8pt]&=\left[{\cfrac {\partial S_{i}^{~j}}{\partial q^{k}}}-\Gamma _{ik}^{l}~S_{l}^{~j}+\Gamma _{kl}^{j}~S_{i}^{~l}\right]~g^{ik}~\mathbf {b} _{j}\end{aligned}}}
Cylindrical polar coordinates
In cylindrical polar coordinates
∇
⋅
v
=
∂
v
r
∂
r
+
1
r
(
∂
v
θ
∂
θ
+
v
r
)
+
∂
v
z
∂
z
∇
⋅
S
=
∂
S
r
r
∂
r
e
r
+
∂
S
r
θ
∂
r
e
θ
+
∂
S
r
z
∂
r
e
z
+
1
r
[
∂
S
θ
r
∂
θ
+
(
S
r
r
−
S
θ
θ
)
]
e
r
+
1
r
[
∂
S
θ
θ
∂
θ
+
(
S
r
θ
+
S
θ
r
)
]
e
θ
+
1
r
[
∂
S
θ
z
∂
θ
+
S
r
z
]
e
z
+
∂
S
z
r
∂
z
e
r
+
∂
S
z
θ
∂
z
e
θ
+
∂
S
z
z
∂
z
e
z
{\displaystyle {\begin{aligned}{\boldsymbol {\nabla }}\cdot \mathbf {v} =\quad &{\frac {\partial v_{r}}{\partial r}}+{\frac {1}{r}}\left({\frac {\partial v_{\theta }}{\partial \theta }}+v_{r}\right)+{\frac {\partial v_{z}}{\partial z}}\\{\boldsymbol {\nabla }}\cdot {\boldsymbol {S}}=\quad &{\frac {\partial S_{rr}}{\partial r}}~\mathbf {e} _{r}+{\frac {\partial S_{r\theta }}{\partial r}}~\mathbf {e} _{\theta }+{\frac {\partial S_{rz}}{\partial r}}~\mathbf {e} _{z}\\{}+{}&{\frac {1}{r}}\left[{\frac {\partial S_{\theta r}}{\partial \theta }}+(S_{rr}-S_{\theta \theta })\right]~\mathbf {e} _{r}+{\frac {1}{r}}\left[{\frac {\partial S_{\theta \theta }}{\partial \theta }}+(S_{r\theta }+S_{\theta r})\right]~\mathbf {e} _{\theta }+{\frac {1}{r}}\left[{\frac {\partial S_{\theta z}}{\partial \theta }}+S_{rz}\right]~\mathbf {e} _{z}\\{}+{}&{\frac {\partial S_{zr}}{\partial z}}~\mathbf {e} _{r}+{\frac {\partial S_{z\theta }}{\partial z}}~\mathbf {e} _{\theta }+{\frac {\partial S_{zz}}{\partial z}}~\mathbf {e} _{z}\end{aligned}}}
Curl of a tensor field
The curl of an order-n > 1 tensor field
T
(
x
)
{\displaystyle {\boldsymbol {T}}(\mathbf {x} )}
(
∇
×
T
)
⋅
c
=
∇
×
(
c
⋅
T
)
;
(
∇
×
v
)
⋅
c
=
∇
⋅
(
v
×
c
)
{\displaystyle ({\boldsymbol {\nabla }}\times {\boldsymbol {T}})\cdot \mathbf {c} ={\boldsymbol {\nabla }}\times (\mathbf {c} \cdot {\boldsymbol {T}})~;\qquad ({\boldsymbol {\nabla }}\times \mathbf {v} )\cdot \mathbf {c} ={\boldsymbol {\nabla }}\cdot (\mathbf {v} \times \mathbf {c} )}
c is an arbitrary constant vector and v is a vector field.
Consider a vector field v and an arbitrary constant vector c . In index notation, the cross product is given by
v
×
c
=
ε
i
j
k
v
j
c
k
e
i
{\displaystyle \mathbf {v} \times \mathbf {c} =\varepsilon _{ijk}~v_{j}~c_{k}~\mathbf {e} _{i}}
ε
i
j
k
{\displaystyle \varepsilon _{ijk}}
permutation symbol , otherwise known as the Levi-Civita symbol. Then,
∇
⋅
(
v
×
c
)
=
ε
i
j
k
v
j
,
i
c
k
=
(
ε
i
j
k
v
j
,
i
e
k
)
⋅
c
=
(
∇
×
v
)
⋅
c
{\displaystyle {\boldsymbol {\nabla }}\cdot (\mathbf {v} \times \mathbf {c} )=\varepsilon _{ijk}~v_{j,i}~c_{k}=(\varepsilon _{ijk}~v_{j,i}~\mathbf {e} _{k})\cdot \mathbf {c} =({\boldsymbol {\nabla }}\times \mathbf {v} )\cdot \mathbf {c} }
∇
×
v
=
ε
i
j
k
v
j
,
i
e
k
{\displaystyle {\boldsymbol {\nabla }}\times \mathbf {v} =\varepsilon _{ijk}~v_{j,i}~\mathbf {e} _{k}}
Curl of a second-order tensor field
For a second-order tensor
S
{\displaystyle {\boldsymbol {S}}}
c
⋅
S
=
c
m
S
m
j
e
j
{\displaystyle \mathbf {c} \cdot {\boldsymbol {S}}=c_{m}~S_{mj}~\mathbf {e} _{j}}
∇
×
(
c
⋅
S
)
=
ε
i
j
k
c
m
S
m
j
,
i
e
k
=
(
ε
i
j
k
S
m
j
,
i
e
k
⊗
e
m
)
⋅
c
=
(
∇
×
S
)
⋅
c
{\displaystyle {\boldsymbol {\nabla }}\times (\mathbf {c} \cdot {\boldsymbol {S}})=\varepsilon _{ijk}~c_{m}~S_{mj,i}~\mathbf {e} _{k}=(\varepsilon _{ijk}~S_{mj,i}~\mathbf {e} _{k}\otimes \mathbf {e} _{m})\cdot \mathbf {c} =({\boldsymbol {\nabla }}\times {\boldsymbol {S}})\cdot \mathbf {c} }
∇
×
S
=
ε
i
j
k
S
m
j
,
i
e
k
⊗
e
m
{\displaystyle {\boldsymbol {\nabla }}\times {\boldsymbol {S}}=\varepsilon _{ijk}~S_{mj,i}~\mathbf {e} _{k}\otimes \mathbf {e} _{m}}
Identities involving the curl of a tensor field
The most commonly used identity involving the curl of a tensor field,
T
{\displaystyle {\boldsymbol {T}}}
∇
×
(
∇
T
)
=
0
{\displaystyle {\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}{\boldsymbol {T}})={\boldsymbol {0}}}
S
{\displaystyle {\boldsymbol {S}}}
∇
×
(
∇
S
)
=
0
⟹
S
m
i
,
j
−
S
m
j
,
i
=
0
{\displaystyle {\boldsymbol {\nabla }}\times ({\boldsymbol {\nabla }}{\boldsymbol {S}})={\boldsymbol {0}}\quad \implies \quad S_{mi,j}-S_{mj,i}=0}
Derivative of the determinant of a second-order tensor
The derivative of the determinant of a second order tensor
A
{\displaystyle {\boldsymbol {A}}}
∂
∂
A
det
(
A
)
=
det
(
A
)
[
A
−
1
]
T
.
{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det({\boldsymbol {A}})=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}
In an orthonormal basis, the components of
A
{\displaystyle {\boldsymbol {A}}}
A . In that case, the right hand side corresponds the cofactors of the matrix.
Derivatives of the invariants of a second-order tensor
The principal invariants of a second order tensor are
I
1
(
A
)
=
tr
A
I
2
(
A
)
=
1
2
[
(
tr
A
)
2
−
tr
A
2
]
I
3
(
A
)
=
det
(
A
)
{\displaystyle {\begin{aligned}I_{1}({\boldsymbol {A}})&={\text{tr}}{\boldsymbol {A}}\\I_{2}({\boldsymbol {A}})&={\tfrac {1}{2}}\left[({\text{tr}}{\boldsymbol {A}})^{2}-{\text{tr}}{{\boldsymbol {A}}^{2}}\right]\\I_{3}({\boldsymbol {A}})&=\det({\boldsymbol {A}})\end{aligned}}}
The derivatives of these three invariants with respect to
A
{\displaystyle {\boldsymbol {A}}}
∂
I
1
∂
A
=
1
∂
I
2
∂
A
=
I
1
1
−
A
T
∂
I
3
∂
A
=
det
(
A
)
[
A
−
1
]
T
=
I
2
1
−
A
T
(
I
1
1
−
A
T
)
=
(
A
2
−
I
1
A
+
I
2
1
)
T
{\displaystyle {\begin{aligned}{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}&={\boldsymbol {\mathit {1}}}\\[3pt]{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}&=I_{1}\,{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\\[3pt]{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}&=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}\\&=I_{2}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}~\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\right)=\left({\boldsymbol {A}}^{2}-I_{1}~{\boldsymbol {A}}+I_{2}~{\boldsymbol {\mathit {1}}}\right)^{\textsf {T}}\end{aligned}}}
Proof
From the derivative of the determinant we know that
∂
I
3
∂
A
=
det
(
A
)
[
A
−
1
]
T
.
{\displaystyle {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det({\boldsymbol {A}})~\left[{\boldsymbol {A}}^{-1}\right]^{\textsf {T}}~.}
For the derivatives of the other two invariants, let us go back to the characteristic equation
det
(
λ
1
+
A
)
=
λ
3
+
I
1
(
A
)
λ
2
+
I
2
(
A
)
λ
+
I
3
(
A
)
.
{\displaystyle \det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})=\lambda ^{3}+I_{1}({\boldsymbol {A}})~\lambda ^{2}+I_{2}({\boldsymbol {A}})~\lambda +I_{3}({\boldsymbol {A}})~.}
Using the same approach as for the determinant of a tensor, we can show that
∂
∂
A
det
(
λ
1
+
A
)
=
det
(
λ
1
+
A
)
[
(
λ
1
+
A
)
−
1
]
T
.
{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}\right]^{\textsf {T}}~.}
Now the left hand side can be expanded as
∂
∂
A
det
(
λ
1
+
A
)
=
∂
∂
A
[
λ
3
+
I
1
(
A
)
λ
2
+
I
2
(
A
)
λ
+
I
3
(
A
)
]
=
∂
I
1
∂
A
λ
2
+
∂
I
2
∂
A
λ
+
∂
I
3
∂
A
.
{\displaystyle {\begin{aligned}{\frac {\partial }{\partial {\boldsymbol {A}}}}\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})&={\frac {\partial }{\partial {\boldsymbol {A}}}}\left[\lambda ^{3}+I_{1}({\boldsymbol {A}})~\lambda ^{2}+I_{2}({\boldsymbol {A}})~\lambda +I_{3}({\boldsymbol {A}})\right]\\&={\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~.\end{aligned}}}
Hence
∂
I
1
∂
A
λ
2
+
∂
I
2
∂
A
λ
+
∂
I
3
∂
A
=
det
(
λ
1
+
A
)
[
(
λ
1
+
A
)
−
1
]
T
{\displaystyle {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~\left[(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{-1}\right]^{\textsf {T}}}
(
λ
1
+
A
)
T
⋅
[
∂
I
1
∂
A
λ
2
+
∂
I
2
∂
A
λ
+
∂
I
3
∂
A
]
=
det
(
λ
1
+
A
)
1
.
{\displaystyle (\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})^{\textsf {T}}\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\det(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}})~{\boldsymbol {\mathit {1}}}~.}
Expanding the right hand side and separating terms on the left hand side gives
(
λ
1
+
A
T
)
⋅
[
∂
I
1
∂
A
λ
2
+
∂
I
2
∂
A
λ
+
∂
I
3
∂
A
]
=
[
λ
3
+
I
1
λ
2
+
I
2
λ
+
I
3
]
1
{\displaystyle \left(\lambda ~{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\right)\cdot \left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right]=\left[\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}}
or,
[
∂
I
1
∂
A
λ
3
+
∂
I
2
∂
A
λ
2
+
∂
I
3
∂
A
λ
]
1
+
A
T
⋅
∂
I
1
∂
A
λ
2
+
A
T
⋅
∂
I
2
∂
A
λ
+
A
T
⋅
∂
I
3
∂
A
=
[
λ
3
+
I
1
λ
2
+
I
2
λ
+
I
3
]
1
.
{\displaystyle {\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.&\left.+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~\lambda \right]{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\&=\left[\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}~.\end{aligned}}}
If we define
I
0
:=
1
{\displaystyle I_{0}:=1}
I
4
:=
0
{\displaystyle I_{4}:=0}
[
∂
I
1
∂
A
λ
3
+
∂
I
2
∂
A
λ
2
+
∂
I
3
∂
A
λ
+
∂
I
4
∂
A
]
1
+
A
T
⋅
∂
I
0
∂
A
λ
3
+
A
T
⋅
∂
I
1
∂
A
λ
2
+
A
T
⋅
∂
I
2
∂
A
λ
+
A
T
⋅
∂
I
3
∂
A
=
[
I
0
λ
3
+
I
1
λ
2
+
I
2
λ
+
I
3
]
1
.
{\displaystyle {\begin{aligned}\left[{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}\right.&\left.+{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~\lambda +{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}\right]{\boldsymbol {\mathit {1}}}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{0}}{\partial {\boldsymbol {A}}}}~\lambda ^{3}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~\lambda ^{2}+{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~\lambda +{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\\&=\left[I_{0}~\lambda ^{3}+I_{1}~\lambda ^{2}+I_{2}~\lambda +I_{3}\right]{\boldsymbol {\mathit {1}}}~.\end{aligned}}}
Collecting terms containing various powers of λ, we get
λ
3
(
I
0
1
−
∂
I
1
∂
A
1
−
A
T
⋅
∂
I
0
∂
A
)
+
λ
2
(
I
1
1
−
∂
I
2
∂
A
1
−
A
T
⋅
∂
I
1
∂
A
)
+
λ
(
I
2
1
−
∂
I
3
∂
A
1
−
A
T
⋅
∂
I
2
∂
A
)
+
(
I
3
1
−
∂
I
4
∂
A
1
−
A
T
⋅
∂
I
3
∂
A
)
=
0
.
{\displaystyle {\begin{aligned}\lambda ^{3}&\left(I_{0}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{0}}{\partial {\boldsymbol {A}}}}\right)+\lambda ^{2}\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}\right)+\\&\qquad \qquad \lambda \left(I_{2}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}\right)+\left(I_{3}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}\right)=0~.\end{aligned}}}
Then, invoking the arbitrariness of λ, we have
I
0
1
−
∂
I
1
∂
A
1
−
A
T
⋅
∂
I
0
∂
A
=
0
I
1
1
−
∂
I
2
∂
A
1
−
I
2
1
−
∂
I
3
∂
A
1
−
A
T
⋅
∂
I
2
∂
A
=
0
I
3
1
−
∂
I
4
∂
A
1
−
A
T
⋅
∂
I
3
∂
A
=
0
.
{\displaystyle {\begin{aligned}I_{0}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{0}}{\partial {\boldsymbol {A}}}}&=0\\I_{1}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-I_{2}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}&=0\\I_{3}~{\boldsymbol {\mathit {1}}}-{\frac {\partial I_{4}}{\partial {\boldsymbol {A}}}}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\cdot {\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}&=0~.\end{aligned}}}
This implies that
∂
I
1
∂
A
=
1
∂
I
2
∂
A
=
I
1
1
−
A
T
∂
I
3
∂
A
=
I
2
1
−
A
T
(
I
1
1
−
A
T
)
=
(
A
2
−
I
1
A
+
I
2
1
)
T
{\displaystyle {\begin{aligned}{\frac {\partial I_{1}}{\partial {\boldsymbol {A}}}}&={\boldsymbol {\mathit {1}}}\\{\frac {\partial I_{2}}{\partial {\boldsymbol {A}}}}&=I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\\{\frac {\partial I_{3}}{\partial {\boldsymbol {A}}}}&=I_{2}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}~\left(I_{1}~{\boldsymbol {\mathit {1}}}-{\boldsymbol {A}}^{\textsf {T}}\right)=\left({\boldsymbol {A}}^{2}-I_{1}~{\boldsymbol {A}}+I_{2}~{\boldsymbol {\mathit {1}}}\right)^{\textsf {T}}\end{aligned}}}
Derivative of the second-order identity tensor
Let
1
{\displaystyle {\boldsymbol {\mathit {1}}}}
A
{\displaystyle {\boldsymbol {A}}}
∂
1
∂
A
:
T
=
0
:
T
=
0
{\displaystyle {\frac {\partial {\boldsymbol {\mathit {1}}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}={\boldsymbol {\mathsf {0}}}:{\boldsymbol {T}}={\boldsymbol {\mathit {0}}}}
1
{\displaystyle {\boldsymbol {\mathit {1}}}}
A
{\displaystyle {\boldsymbol {A}}}
Derivative of a second-order tensor with respect to itself
Let
A
{\displaystyle {\boldsymbol {A}}}
∂
A
∂
A
:
T
=
[
∂
∂
α
(
A
+
α
T
)
]
α
=
0
=
T
=
I
:
T
{\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}=\left[{\frac {\partial }{\partial \alpha }}({\boldsymbol {A}}+\alpha ~{\boldsymbol {T}})\right]_{\alpha =0}={\boldsymbol {T}}={\boldsymbol {\mathsf {I}}}:{\boldsymbol {T}}}
Therefore,
∂
A
∂
A
=
I
{\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}={\boldsymbol {\mathsf {I}}}}
Here
I
{\displaystyle {\boldsymbol {\mathsf {I}}}}
I
=
δ
i
k
δ
j
l
e
i
⊗
e
j
⊗
e
k
⊗
e
l
{\displaystyle {\boldsymbol {\mathsf {I}}}=\delta _{ik}~\delta _{jl}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{l}}
This result implies that
∂
A
T
∂
A
:
T
=
I
T
:
T
=
T
T
{\displaystyle {\frac {\partial {\boldsymbol {A}}^{\textsf {T}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}={\boldsymbol {\mathsf {I}}}^{\textsf {T}}:{\boldsymbol {T}}={\boldsymbol {T}}^{\textsf {T}}}
I
T
=
δ
j
k
δ
i
l
e
i
⊗
e
j
⊗
e
k
⊗
e
l
{\displaystyle {\boldsymbol {\mathsf {I}}}^{\textsf {T}}=\delta _{jk}~\delta _{il}~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{l}}
Therefore, if the tensor
A
{\displaystyle {\boldsymbol {A}}}
∂
A
∂
A
=
I
(
s
)
=
1
2
(
I
+
I
T
)
{\displaystyle {\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}={\boldsymbol {\mathsf {I}}}^{(s)}={\frac {1}{2}}~\left({\boldsymbol {\mathsf {I}}}+{\boldsymbol {\mathsf {I}}}^{\textsf {T}}\right)}
I
(
s
)
=
1
2
(
δ
i
k
δ
j
l
+
δ
i
l
δ
j
k
)
e
i
⊗
e
j
⊗
e
k
⊗
e
l
{\displaystyle {\boldsymbol {\mathsf {I}}}^{(s)}={\frac {1}{2}}~(\delta _{ik}~\delta _{jl}+\delta _{il}~\delta _{jk})~\mathbf {e} _{i}\otimes \mathbf {e} _{j}\otimes \mathbf {e} _{k}\otimes \mathbf {e} _{l}}
Derivative of the inverse of a second-order tensor
Let
A
{\displaystyle {\boldsymbol {A}}}
T
{\displaystyle {\boldsymbol {T}}}
∂
∂
A
(
A
−
1
)
:
T
=
−
A
−
1
⋅
T
⋅
A
−
1
{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\left({\boldsymbol {A}}^{-1}\right):{\boldsymbol {T}}=-{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\cdot {\boldsymbol {A}}^{-1}}
∂
A
i
j
−
1
∂
A
k
l
T
k
l
=
−
A
i
k
−
1
T
k
l
A
l
j
−
1
⟹
∂
A
i
j
−
1
∂
A
k
l
=
−
A
i
k
−
1
A
l
j
−
1
{\displaystyle {\frac {\partial A_{ij}^{-1}}{\partial A_{kl}}}~T_{kl}=-A_{ik}^{-1}~T_{kl}~A_{lj}^{-1}\implies {\frac {\partial A_{ij}^{-1}}{\partial A_{kl}}}=-A_{ik}^{-1}~A_{lj}^{-1}}
∂
∂
A
(
A
−
T
)
:
T
=
−
A
−
T
⋅
T
T
⋅
A
−
T
{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\left({\boldsymbol {A}}^{-{\textsf {T}}}\right):{\boldsymbol {T}}=-{\boldsymbol {A}}^{-{\textsf {T}}}\cdot {\boldsymbol {T}}^{\textsf {T}}\cdot {\boldsymbol {A}}^{-{\textsf {T}}}}
∂
A
j
i
−
1
∂
A
k
l
T
k
l
=
−
A
j
k
−
1
T
l
k
A
l
i
−
1
⟹
∂
A
j
i
−
1
∂
A
k
l
=
−
A
l
i
−
1
A
j
k
−
1
{\displaystyle {\frac {\partial A_{ji}^{-1}}{\partial A_{kl}}}~T_{kl}=-A_{jk}^{-1}~T_{lk}~A_{li}^{-1}\implies {\frac {\partial A_{ji}^{-1}}{\partial A_{kl}}}=-A_{li}^{-1}~A_{jk}^{-1}}
A
{\displaystyle {\boldsymbol {A}}}
∂
A
i
j
−
1
∂
A
k
l
=
−
1
2
(
A
i
k
−
1
A
j
l
−
1
+
A
i
l
−
1
A
j
k
−
1
)
{\displaystyle {\frac {\partial A_{ij}^{-1}}{\partial A_{kl}}}=-{\cfrac {1}{2}}\left(A_{ik}^{-1}~A_{jl}^{-1}+A_{il}^{-1}~A_{jk}^{-1}\right)}
Proof
Recall that
∂
1
∂
A
:
T
=
0
{\displaystyle {\frac {\partial {\boldsymbol {\mathit {1}}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}={\boldsymbol {\mathit {0}}}}
Since
A
−
1
⋅
A
=
1
{\displaystyle {\boldsymbol {A}}^{-1}\cdot {\boldsymbol {A}}={\boldsymbol {\mathit {1}}}}
∂
∂
A
(
A
−
1
⋅
A
)
:
T
=
0
{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\left({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {A}}\right):{\boldsymbol {T}}={\boldsymbol {\mathit {0}}}}
Using the product rule for second order tensors
∂
∂
S
[
F
1
(
S
)
⋅
F
2
(
S
)
]
:
T
=
(
∂
F
1
∂
S
:
T
)
⋅
F
2
+
F
1
⋅
(
∂
F
2
∂
S
:
T
)
{\displaystyle {\frac {\partial }{\partial {\boldsymbol {S}}}}[{\boldsymbol {F}}_{1}({\boldsymbol {S}})\cdot {\boldsymbol {F}}_{2}({\boldsymbol {S}})]:{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {F}}_{1}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {F}}_{2}+{\boldsymbol {F}}_{1}\cdot \left({\frac {\partial {\boldsymbol {F}}_{2}}{\partial {\boldsymbol {S}}}}:{\boldsymbol {T}}\right)}
we get
∂
∂
A
(
A
−
1
⋅
A
)
:
T
=
(
∂
A
−
1
∂
A
:
T
)
⋅
A
+
A
−
1
⋅
(
∂
A
∂
A
:
T
)
=
0
{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}({\boldsymbol {A}}^{-1}\cdot {\boldsymbol {A}}):{\boldsymbol {T}}=\left({\frac {\partial {\boldsymbol {A}}^{-1}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {A}}+{\boldsymbol {A}}^{-1}\cdot \left({\frac {\partial {\boldsymbol {A}}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}\right)={\boldsymbol {\mathit {0}}}}
(
∂
A
−
1
∂
A
:
T
)
⋅
A
=
−
A
−
1
⋅
T
{\displaystyle \left({\frac {\partial {\boldsymbol {A}}^{-1}}{\partial {\boldsymbol {A}}}}:{\boldsymbol {T}}\right)\cdot {\boldsymbol {A}}=-{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}}
Therefore,
∂
∂
A
(
A
−
1
)
:
T
=
−
A
−
1
⋅
T
⋅
A
−
1
{\displaystyle {\frac {\partial }{\partial {\boldsymbol {A}}}}\left({\boldsymbol {A}}^{-1}\right):{\boldsymbol {T}}=-{\boldsymbol {A}}^{-1}\cdot {\boldsymbol {T}}\cdot {\boldsymbol {A}}^{-1}}
Integration by parts
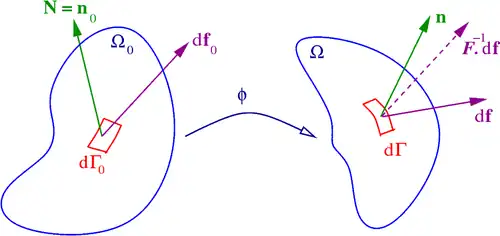
Domain
Ω
{\displaystyle \Omega }
Γ
{\displaystyle \Gamma }
n
{\displaystyle \mathbf {n} }
Another important operation related to tensor derivatives in continuum mechanics is integration by parts. The formula for integration by parts can be written as
∫
Ω
F
⊗
∇
G
d
Ω
=
∫
Γ
n
⊗
(
F
⊗
G
)
d
Γ
−
∫
Ω
G
⊗
∇
F
d
Ω
{\displaystyle \int _{\Omega }{\boldsymbol {F}}\otimes {\boldsymbol {\nabla }}{\boldsymbol {G}}\,d\Omega =\int _{\Gamma }\mathbf {n} \otimes ({\boldsymbol {F}}\otimes {\boldsymbol {G}})\,d\Gamma -\int _{\Omega }{\boldsymbol {G}}\otimes {\boldsymbol {\nabla }}{\boldsymbol {F}}\,d\Omega }
where
F
{\displaystyle {\boldsymbol {F}}}
G
{\displaystyle {\boldsymbol {G}}}
n
{\displaystyle \mathbf {n} }
⊗
{\displaystyle \otimes }
∇
{\displaystyle {\boldsymbol {\nabla }}}
F
{\displaystyle {\boldsymbol {F}}}
divergence theorem
∫
Ω
∇
G
d
Ω
=
∫
Γ
n
⊗
G
d
Γ
.
{\displaystyle \int _{\Omega }{\boldsymbol {\nabla }}{\boldsymbol {G}}\,d\Omega =\int _{\Gamma }\mathbf {n} \otimes {\boldsymbol {G}}\,d\Gamma \,.}
We can express the formula for integration by parts in Cartesian index notation as
∫
Ω
F
i
j
k
.
.
.
.
G
l
m
n
.
.
.
,
p
d
Ω
=
∫
Γ
n
p
F
i
j
k
.
.
.
G
l
m
n
.
.
.
d
Γ
−
∫
Ω
G
l
m
n
.
.
.
F
i
j
k
.
.
.
,
p
d
Ω
.
{\displaystyle \int _{\Omega }F_{ijk....}\,G_{lmn...,p}\,d\Omega =\int _{\Gamma }n_{p}\,F_{ijk...}\,G_{lmn...}\,d\Gamma -\int _{\Omega }G_{lmn...}\,F_{ijk...,p}\,d\Omega \,.}
For the special case where the tensor product operation is a contraction of one index and the gradient operation is a divergence, and both
F
{\displaystyle {\boldsymbol {F}}}
G
{\displaystyle {\boldsymbol {G}}}
∫
Ω
F
⋅
(
∇
⋅
G
)
d
Ω
=
∫
Γ
n
⋅
(
G
⋅
F
T
)
d
Γ
−
∫
Ω
(
∇
F
)
:
G
T
d
Ω
.
{\displaystyle \int _{\Omega }{\boldsymbol {F}}\cdot ({\boldsymbol {\nabla }}\cdot {\boldsymbol {G}})\,d\Omega =\int _{\Gamma }\mathbf {n} \cdot \left({\boldsymbol {G}}\cdot {\boldsymbol {F}}^{\textsf {T}}\right)\,d\Gamma -\int _{\Omega }({\boldsymbol {\nabla }}{\boldsymbol {F}}):{\boldsymbol {G}}^{\textsf {T}}\,d\Omega \,.}
∫
Ω
F
i
j
G
p
j
,
p
d
Ω
=
∫
Γ
n
p
F
i
j
G
p
j
d
Γ
−
∫
Ω
G
p
j
F
i
j
,
p
d
Ω
.
{\displaystyle \int _{\Omega }F_{ij}\,G_{pj,p}\,d\Omega =\int _{\Gamma }n_{p}\,F_{ij}\,G_{pj}\,d\Gamma -\int _{\Omega }G_{pj}\,F_{ij,p}\,d\Omega \,.}
See also
References
^ Simo, J. C.; Hughes, T. J. R. (1998). Computational Inelasticity . Springer. doi :10.1007/b98904 . ISBN 978-0-387-97520-7 . ^ Marsden, Jerrold E.; Hughes, Thomas J. R. (2000). Mathematical Foundations of Elasticity . Dover. ISBN 978-0-486-678658 . ^ Ogden, R. W. (2000). Nonlinear Elastic Deformations . Dover. ISBN 978-0-486-696485 . ^ a b Hjelmstad, Keith (2004). Fundamentals of Structural Mechanics . Springer Science & Business Media. p. 45. ISBN 978-0-387-233307 .