In continuum mechanics , a Mooney–Rivlin solid [ 1] [ 2] hyperelastic material model where the strain energy density function
W
{\displaystyle W\,}
invariants of the left Cauchy–Green deformation tensor
B
{\displaystyle {\boldsymbol {B}}}
Melvin Mooney in 1940 and expressed in terms of invariants by Ronald Rivlin in 1948.
The strain energy density function for an incompressible Mooney–Rivlin material is[ 3] [ 4]
W
=
C
1
(
I
¯
1
−
3
)
+
C
2
(
I
¯
2
−
3
)
,
{\displaystyle W=C_{1}({\bar {I}}_{1}-3)+C_{2}({\bar {I}}_{2}-3),\,}
where
C
1
{\displaystyle C_{1}}
C
2
{\displaystyle C_{2}}
I
¯
1
{\displaystyle {\bar {I}}_{1}}
I
¯
2
{\displaystyle {\bar {I}}_{2}}
invariant of
B
¯
=
(
det
B
)
−
1
/
3
B
{\displaystyle {\bar {\boldsymbol {B}}}=(\det {\boldsymbol {B}})^{-1/3}{\boldsymbol {B}}}
unimodular component of
B
{\displaystyle {\boldsymbol {B}}}
[ 5]
I
¯
1
=
J
−
2
/
3
I
1
,
I
1
=
λ
1
2
+
λ
2
2
+
λ
3
2
,
I
¯
2
=
J
−
4
/
3
I
2
,
I
2
=
λ
1
2
λ
2
2
+
λ
2
2
λ
3
2
+
λ
3
2
λ
1
2
{\displaystyle {\begin{aligned}{\bar {I}}_{1}&=J^{-2/3}~I_{1},\quad I_{1}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2},\\{\bar {I}}_{2}&=J^{-4/3}~I_{2},\quad I_{2}=\lambda _{1}^{2}\lambda _{2}^{2}+\lambda _{2}^{2}\lambda _{3}^{2}+\lambda _{3}^{2}\lambda _{1}^{2}\end{aligned}}}
where
F
{\displaystyle {\boldsymbol {F}}}
deformation gradient and
J
=
det
(
F
)
=
λ
1
λ
2
λ
3
{\displaystyle J=\det({\boldsymbol {F}})=\lambda _{1}\lambda _{2}\lambda _{3}}
J
=
1
{\displaystyle J=1}
Derivation
The Mooney–Rivlin model is a special case of the generalized Rivlin model (also called polynomial hyperelastic model [ 6]
W
=
∑
p
,
q
=
0
N
C
p
q
(
I
¯
1
−
3
)
p
(
I
¯
2
−
3
)
q
+
∑
m
=
1
M
1
D
m
(
J
−
1
)
2
m
{\displaystyle W=\sum _{p,q=0}^{N}C_{pq}({\bar {I}}_{1}-3)^{p}~({\bar {I}}_{2}-3)^{q}+\sum _{m=1}^{M}{\frac {1}{D_{m}}}~(J-1)^{2m}}
with
C
00
=
0
{\displaystyle C_{00}=0}
C
p
q
{\displaystyle C_{pq}}
D
m
{\displaystyle D_{m}}
compressible Mooney–Rivlin material
N
=
1
,
C
01
=
C
2
,
C
11
=
0
,
C
10
=
C
1
,
M
=
1
{\displaystyle N=1,C_{01}=C_{2},C_{11}=0,C_{10}=C_{1},M=1}
W
=
C
01
(
I
¯
2
−
3
)
+
C
10
(
I
¯
1
−
3
)
+
1
D
1
(
J
−
1
)
2
{\displaystyle W=C_{01}~({\bar {I}}_{2}-3)+C_{10}~({\bar {I}}_{1}-3)+{\frac {1}{D_{1}}}~(J-1)^{2}}
If
C
01
=
0
{\displaystyle C_{01}=0}
neo-Hookean solid , a special case of a Mooney–Rivlin solid .
For consistency with linear elasticity in the limit of small strains , it is necessary that
κ
=
2
/
D
1
;
μ
=
2
(
C
01
+
C
10
)
{\displaystyle \kappa =2/D_{1}~;~~\mu =2~(C_{01}+C_{10})}
where
κ
{\displaystyle \kappa }
bulk modulus and
μ
{\displaystyle \mu }
shear modulus .
The Cauchy stress in a compressible hyperelastic material with a stress free reference configuration is given by
σ
=
2
J
[
1
J
2
/
3
(
∂
W
∂
I
¯
1
+
I
¯
1
∂
W
∂
I
¯
2
)
B
−
1
J
4
/
3
∂
W
∂
I
¯
2
B
⋅
B
]
+
[
∂
W
∂
J
−
2
3
J
(
I
¯
1
∂
W
∂
I
¯
1
+
2
I
¯
2
∂
W
∂
I
¯
2
)
]
I
{\displaystyle {\boldsymbol {\sigma }}={\cfrac {2}{J}}\left[{\cfrac {1}{J^{2/3}}}\left({\cfrac {\partial {W}}{\partial {\bar {I}}_{1}}}+{\bar {I}}_{1}~{\cfrac {\partial {W}}{\partial {\bar {I}}_{2}}}\right){\boldsymbol {B}}-{\cfrac {1}{J^{4/3}}}~{\cfrac {\partial {W}}{\partial {\bar {I}}_{2}}}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+\left[{\cfrac {\partial {W}}{\partial J}}-{\cfrac {2}{3J}}\left({\bar {I}}_{1}~{\cfrac {\partial {W}}{\partial {\bar {I}}_{1}}}+2~{\bar {I}}_{2}~{\cfrac {\partial {W}}{\partial {\bar {I}}_{2}}}\right)\right]~{\boldsymbol {I}}}
For a compressible Mooney–Rivlin material,
∂
W
∂
I
¯
1
=
C
1
;
∂
W
∂
I
¯
2
=
C
2
;
∂
W
∂
J
=
2
D
1
(
J
−
1
)
{\displaystyle {\cfrac {\partial {W}}{\partial {\bar {I}}_{1}}}=C_{1}~;~~{\cfrac {\partial {W}}{\partial {\bar {I}}_{2}}}=C_{2}~;~~{\cfrac {\partial {W}}{\partial J}}={\frac {2}{D_{1}}}(J-1)}
Therefore, the Cauchy stress in a compressible Mooney–Rivlin material is given by
σ
=
2
J
[
1
J
2
/
3
(
C
1
+
I
¯
1
C
2
)
B
−
1
J
4
/
3
C
2
B
⋅
B
]
+
[
2
D
1
(
J
−
1
)
−
2
3
J
(
C
1
I
¯
1
+
2
C
2
I
¯
2
)
]
I
{\displaystyle {\boldsymbol {\sigma }}={\cfrac {2}{J}}\left[{\cfrac {1}{J^{2/3}}}\left(C_{1}+{\bar {I}}_{1}~C_{2}\right){\boldsymbol {B}}-{\cfrac {1}{J^{4/3}}}~C_{2}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}\right]+\left[{\frac {2}{D_{1}}}(J-1)-{\cfrac {2}{3J}}\left(C_{1}{\bar {I}}_{1}+2C_{2}{\bar {I}}_{2}~\right)\right]{\boldsymbol {I}}}
It can be shown, after some algebra, that the pressure is given by
p
:=
−
1
3
tr
(
σ
)
=
−
∂
W
∂
J
=
−
2
D
1
(
J
−
1
)
.
{\displaystyle p:=-{\tfrac {1}{3}}\,{\text{tr}}({\boldsymbol {\sigma }})=-{\frac {\partial W}{\partial J}}=-{\frac {2}{D_{1}}}(J-1)\,.}
The stress can then be expressed in the form
σ
=
−
p
I
+
1
J
[
2
J
2
/
3
(
C
1
+
I
¯
1
C
2
)
B
−
2
J
4
/
3
C
2
B
⋅
B
−
2
3
(
C
1
I
¯
1
+
2
C
2
I
¯
2
)
I
]
.
{\displaystyle {\boldsymbol {\sigma }}=-p~{\boldsymbol {I}}+{\cfrac {1}{J}}\left[{\cfrac {2}{J^{2/3}}}\left(C_{1}+{\bar {I}}_{1}~C_{2}\right){\boldsymbol {B}}-{\cfrac {2}{J^{4/3}}}~C_{2}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}-{\cfrac {2}{3}}\left(C_{1}\,{\bar {I}}_{1}+2C_{2}\,{\bar {I}}_{2}\right){\boldsymbol {I}}\right]\,.}
The above equation is often written using the unimodular tensor
B
¯
=
J
−
2
/
3
B
{\displaystyle {\bar {\boldsymbol {B}}}=J^{-2/3}\,{\boldsymbol {B}}}
σ
=
−
p
I
+
1
J
[
2
(
C
1
+
I
¯
1
C
2
)
B
¯
−
2
C
2
B
¯
⋅
B
¯
−
2
3
(
C
1
I
¯
1
+
2
C
2
I
¯
2
)
I
]
.
{\displaystyle {\boldsymbol {\sigma }}=-p~{\boldsymbol {I}}+{\cfrac {1}{J}}\left[2\left(C_{1}+{\bar {I}}_{1}~C_{2}\right){\bar {\boldsymbol {B}}}-2~C_{2}~{\bar {\boldsymbol {B}}}\cdot {\bar {\boldsymbol {B}}}-{\cfrac {2}{3}}\left(C_{1}\,{\bar {I}}_{1}+2C_{2}\,{\bar {I}}_{2}\right){\boldsymbol {I}}\right]\,.}
For an incompressible Mooney–Rivlin material with
J
=
1
{\displaystyle J=1}
p
=
0
{\displaystyle p=0}
B
¯
=
B
{\displaystyle {\bar {\boldsymbol {B}}}={\boldsymbol {B}}}
σ
=
2
(
C
1
+
I
1
C
2
)
B
−
2
C
2
B
⋅
B
−
2
3
(
C
1
I
1
+
2
C
2
I
2
)
I
.
{\displaystyle {\boldsymbol {\sigma }}=2\left(C_{1}+I_{1}~C_{2}\right){\boldsymbol {B}}-2C_{2}~{\boldsymbol {B}}\cdot {\boldsymbol {B}}-{\cfrac {2}{3}}\left(C_{1}\,I_{1}+2C_{2}\,I_{2}\right){\boldsymbol {I}}\,.}
Since
det
J
=
1
{\displaystyle \det J=1}
Cayley–Hamilton theorem implies
B
−
1
=
B
⋅
B
−
I
1
B
+
I
2
I
.
{\displaystyle {\boldsymbol {B}}^{-1}={\boldsymbol {B}}\cdot {\boldsymbol {B}}-I_{1}~{\boldsymbol {B}}+I_{2}~{\boldsymbol {I}}.}
Hence, the Cauchy stress can be expressed as
σ
=
−
p
∗
I
+
2
C
1
B
−
2
C
2
B
−
1
{\displaystyle {\boldsymbol {\sigma }}=-p^{*}~{\boldsymbol {I}}+2C_{1}~{\boldsymbol {B}}-2C_{2}~{\boldsymbol {B}}^{-1}}
where
p
∗
:=
2
3
(
C
1
I
1
−
C
2
I
2
)
.
{\displaystyle p^{*}:={\tfrac {2}{3}}(C_{1}~I_{1}-C_{2}~I_{2}).\,}
Cauchy stress in terms of principal stretches
In terms of the principal stretches , the Cauchy stress differences for an incompressible hyperelastic material are given by
σ
11
−
σ
33
=
λ
1
∂
W
∂
λ
1
−
λ
3
∂
W
∂
λ
3
;
σ
22
−
σ
33
=
λ
2
∂
W
∂
λ
2
−
λ
3
∂
W
∂
λ
3
{\displaystyle \sigma _{11}-\sigma _{33}=\lambda _{1}~{\cfrac {\partial {W}}{\partial \lambda _{1}}}-\lambda _{3}~{\cfrac {\partial {W}}{\partial \lambda _{3}}}~;~~\sigma _{22}-\sigma _{33}=\lambda _{2}~{\cfrac {\partial {W}}{\partial \lambda _{2}}}-\lambda _{3}~{\cfrac {\partial {W}}{\partial \lambda _{3}}}}
For an incompressible Mooney-Rivlin material,
W
=
C
1
(
λ
1
2
+
λ
2
2
+
λ
3
2
−
3
)
+
C
2
(
λ
1
2
λ
2
2
+
λ
2
2
λ
3
2
+
λ
3
2
λ
1
2
−
3
)
;
λ
1
λ
2
λ
3
=
1
{\displaystyle W=C_{1}(\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}-3)+C_{2}(\lambda _{1}^{2}\lambda _{2}^{2}+\lambda _{2}^{2}\lambda _{3}^{2}+\lambda _{3}^{2}\lambda _{1}^{2}-3)~;~~\lambda _{1}\lambda _{2}\lambda _{3}=1}
Therefore,
λ
1
∂
W
∂
λ
1
=
2
C
1
λ
1
2
+
2
C
2
λ
1
2
(
λ
2
2
+
λ
3
2
)
;
λ
2
∂
W
∂
λ
2
=
2
C
1
λ
2
2
+
2
C
2
λ
2
2
(
λ
1
2
+
λ
3
2
)
;
λ
3
∂
W
∂
λ
3
=
2
C
1
λ
3
2
+
2
C
2
λ
3
2
(
λ
1
2
+
λ
2
2
)
{\displaystyle \lambda _{1}{\cfrac {\partial {W}}{\partial \lambda _{1}}}=2C_{1}\lambda _{1}^{2}+2C_{2}\lambda _{1}^{2}(\lambda _{2}^{2}+\lambda _{3}^{2})~;~~\lambda _{2}{\cfrac {\partial {W}}{\partial \lambda _{2}}}=2C_{1}\lambda _{2}^{2}+2C_{2}\lambda _{2}^{2}(\lambda _{1}^{2}+\lambda _{3}^{2})~;~~\lambda _{3}{\cfrac {\partial {W}}{\partial \lambda _{3}}}=2C_{1}\lambda _{3}^{2}+2C_{2}\lambda _{3}^{2}(\lambda _{1}^{2}+\lambda _{2}^{2})}
Since
λ
1
λ
2
λ
3
=
1
{\displaystyle \lambda _{1}\lambda _{2}\lambda _{3}=1}
λ
1
∂
W
∂
λ
1
=
2
C
1
λ
1
2
+
2
C
2
(
1
λ
3
2
+
1
λ
2
2
)
;
λ
2
∂
W
∂
λ
2
=
2
C
1
λ
2
2
+
2
C
2
(
1
λ
3
2
+
1
λ
1
2
)
λ
3
∂
W
∂
λ
3
=
2
C
1
λ
3
2
+
2
C
2
(
1
λ
2
2
+
1
λ
1
2
)
{\displaystyle {\begin{aligned}\lambda _{1}{\cfrac {\partial {W}}{\partial \lambda _{1}}}&=2C_{1}\lambda _{1}^{2}+2C_{2}\left({\cfrac {1}{\lambda _{3}^{2}}}+{\cfrac {1}{\lambda _{2}^{2}}}\right)~;~~\lambda _{2}{\cfrac {\partial {W}}{\partial \lambda _{2}}}=2C_{1}\lambda _{2}^{2}+2C_{2}\left({\cfrac {1}{\lambda _{3}^{2}}}+{\cfrac {1}{\lambda _{1}^{2}}}\right)\\\lambda _{3}{\cfrac {\partial {W}}{\partial \lambda _{3}}}&=2C_{1}\lambda _{3}^{2}+2C_{2}\left({\cfrac {1}{\lambda _{2}^{2}}}+{\cfrac {1}{\lambda _{1}^{2}}}\right)\end{aligned}}}
Then the expressions for the Cauchy stress differences become
σ
11
−
σ
33
=
2
C
1
(
λ
1
2
−
λ
3
2
)
−
2
C
2
(
1
λ
1
2
−
1
λ
3
2
)
;
σ
22
−
σ
33
=
2
C
1
(
λ
2
2
−
λ
3
2
)
−
2
C
2
(
1
λ
2
2
−
1
λ
3
2
)
{\displaystyle \sigma _{11}-\sigma _{33}=2C_{1}(\lambda _{1}^{2}-\lambda _{3}^{2})-2C_{2}\left({\cfrac {1}{\lambda _{1}^{2}}}-{\cfrac {1}{\lambda _{3}^{2}}}\right)~;~~\sigma _{22}-\sigma _{33}=2C_{1}(\lambda _{2}^{2}-\lambda _{3}^{2})-2C_{2}\left({\cfrac {1}{\lambda _{2}^{2}}}-{\cfrac {1}{\lambda _{3}^{2}}}\right)}
Uniaxial extension
For the case of an incompressible Mooney–Rivlin material under uniaxial elongation,
λ
1
=
λ
{\displaystyle \lambda _{1}=\lambda \,}
λ
2
=
λ
3
=
1
/
λ
{\displaystyle \lambda _{2}=\lambda _{3}=1/{\sqrt {\lambda }}}
true stress (Cauchy stress) differences can be calculated as:
σ
11
−
σ
33
=
2
C
1
(
λ
2
−
1
λ
)
−
2
C
2
(
1
λ
2
−
λ
)
σ
22
−
σ
33
=
0
{\displaystyle {\begin{aligned}\sigma _{11}-\sigma _{33}&=2C_{1}\left(\lambda ^{2}-{\cfrac {1}{\lambda }}\right)-2C_{2}\left({\cfrac {1}{\lambda ^{2}}}-\lambda \right)\\\sigma _{22}-\sigma _{33}&=0\end{aligned}}}
Simple tension
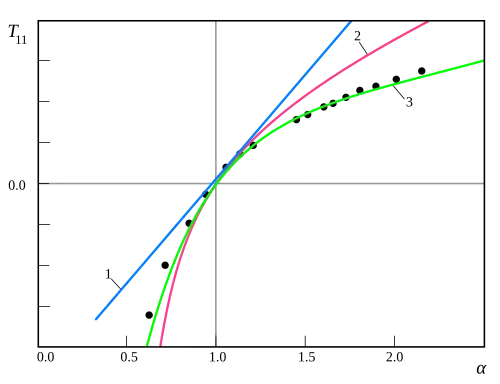
Comparison of experimental results (dots) and predictions for Hooke's law (1, blue line), neo-Hookean solid (2, red line) and Mooney–Rivlin solid models(3, green line) In the case of simple tension,
σ
22
=
σ
33
=
0
{\displaystyle \sigma _{22}=\sigma _{33}=0}
σ
11
=
(
2
C
1
+
2
C
2
λ
)
(
λ
2
−
1
λ
)
{\displaystyle \sigma _{11}=\left(2C_{1}+{\cfrac {2C_{2}}{\lambda }}\right)\left(\lambda ^{2}-{\cfrac {1}{\lambda }}\right)}
In alternative notation, where the Cauchy stress is written as
T
{\displaystyle {\boldsymbol {T}}}
α
{\displaystyle \alpha }
T
11
=
(
2
C
1
+
2
C
2
α
)
(
α
2
−
α
−
1
)
{\displaystyle T_{11}=\left(2C_{1}+{\frac {2C_{2}}{\alpha }}\right)\left(\alpha ^{2}-\alpha ^{-1}\right)}
and the engineering stress (force per unit reference area) for an incompressible Mooney–Rivlin material under simple tension can be calculated using
T
11
e
n
g
=
T
11
α
2
α
3
=
T
11
α
{\displaystyle T_{11}^{\mathrm {eng} }=T_{11}\alpha _{2}\alpha _{3}={\cfrac {T_{11}}{\alpha }}}
T
11
e
n
g
=
(
2
C
1
+
2
C
2
α
)
(
α
−
α
−
2
)
{\displaystyle T_{11}^{\mathrm {eng} }=\left(2C_{1}+{\frac {2C_{2}}{\alpha }}\right)\left(\alpha -\alpha ^{-2}\right)}
If we define
T
11
∗
:=
T
11
e
n
g
α
−
α
−
2
;
β
:=
1
α
{\displaystyle T_{11}^{*}:={\cfrac {T_{11}^{\mathrm {eng} }}{\alpha -\alpha ^{-2}}}~;~~\beta :={\cfrac {1}{\alpha }}}
then
T
11
∗
=
2
C
1
+
2
C
2
β
.
{\displaystyle T_{11}^{*}=2C_{1}+2C_{2}\beta ~.}
The slope of the
T
11
∗
{\displaystyle T_{11}^{*}}
β
{\displaystyle \beta }
C
2
{\displaystyle C_{2}}
T
11
∗
{\displaystyle T_{11}^{*}}
C
1
{\displaystyle C_{1}}
Neo-Hookean solid does, but requires an additional empirical constant.
Equibiaxial tension
In the case of equibiaxial tension, the principal stretches are
λ
1
=
λ
2
=
λ
{\displaystyle \lambda _{1}=\lambda _{2}=\lambda }
λ
3
=
1
/
λ
2
{\displaystyle \lambda _{3}=1/\lambda ^{2}}
σ
11
−
σ
33
=
σ
22
−
σ
33
=
2
C
1
(
λ
2
−
1
λ
4
)
−
2
C
2
(
1
λ
2
−
λ
4
)
{\displaystyle \sigma _{11}-\sigma _{33}=\sigma _{22}-\sigma _{33}=2C_{1}\left(\lambda ^{2}-{\cfrac {1}{\lambda ^{4}}}\right)-2C_{2}\left({\cfrac {1}{\lambda ^{2}}}-\lambda ^{4}\right)}
The equations for equibiaxial tension are equivalent to those governing uniaxial compression.
Pure shear
A pure shear deformation can be achieved by applying stretches of the form [ 7]
λ
1
=
λ
;
λ
2
=
1
λ
;
λ
3
=
1
{\displaystyle \lambda _{1}=\lambda ~;~~\lambda _{2}={\cfrac {1}{\lambda }}~;~~\lambda _{3}=1}
The Cauchy stress differences for pure shear may therefore be expressed as
σ
11
−
σ
33
=
2
C
1
(
λ
2
−
1
)
−
2
C
2
(
1
λ
2
−
1
)
;
σ
22
−
σ
33
=
2
C
1
(
1
λ
2
−
1
)
−
2
C
2
(
λ
2
−
1
)
{\displaystyle \sigma _{11}-\sigma _{33}=2C_{1}(\lambda ^{2}-1)-2C_{2}\left({\cfrac {1}{\lambda ^{2}}}-1\right)~;~~\sigma _{22}-\sigma _{33}=2C_{1}\left({\cfrac {1}{\lambda ^{2}}}-1\right)-2C_{2}(\lambda ^{2}-1)}
Therefore
σ
11
−
σ
22
=
2
(
C
1
+
C
2
)
(
λ
2
−
1
λ
2
)
{\displaystyle \sigma _{11}-\sigma _{22}=2(C_{1}+C_{2})\left(\lambda ^{2}-{\cfrac {1}{\lambda ^{2}}}\right)}
For a pure shear deformation
I
1
=
λ
1
2
+
λ
2
2
+
λ
3
2
=
λ
2
+
1
λ
2
+
1
;
I
2
=
1
λ
1
2
+
1
λ
2
2
+
1
λ
3
2
=
1
λ
2
+
λ
2
+
1
{\displaystyle I_{1}=\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2}=\lambda ^{2}+{\cfrac {1}{\lambda ^{2}}}+1~;~~I_{2}={\cfrac {1}{\lambda _{1}^{2}}}+{\cfrac {1}{\lambda _{2}^{2}}}+{\cfrac {1}{\lambda _{3}^{2}}}={\cfrac {1}{\lambda ^{2}}}+\lambda ^{2}+1}
Therefore
I
1
=
I
2
{\displaystyle I_{1}=I_{2}}
Simple shear
The deformation gradient for a simple shear deformation has the form[ 7]
F
=
1
+
γ
e
1
⊗
e
2
{\displaystyle {\boldsymbol {F}}={\boldsymbol {1}}+\gamma ~\mathbf {e} _{1}\otimes \mathbf {e} _{2}}
where
e
1
,
e
2
{\displaystyle \mathbf {e} _{1},\mathbf {e} _{2}}
γ
=
λ
−
1
λ
;
λ
1
=
λ
;
λ
2
=
1
λ
;
λ
3
=
1
{\displaystyle \gamma =\lambda -{\cfrac {1}{\lambda }}~;~~\lambda _{1}=\lambda ~;~~\lambda _{2}={\cfrac {1}{\lambda }}~;~~\lambda _{3}=1}
In matrix form, the deformation gradient and the left Cauchy-Green deformation tensor may then be expressed as
F
=
[
1
γ
0
0
1
0
0
0
1
]
;
B
=
F
⋅
F
T
=
[
1
+
γ
2
γ
0
γ
1
0
0
0
1
]
{\displaystyle {\boldsymbol {F}}={\begin{bmatrix}1&\gamma &0\\0&1&0\\0&0&1\end{bmatrix}}~;~~{\boldsymbol {B}}={\boldsymbol {F}}\cdot {\boldsymbol {F}}^{T}={\begin{bmatrix}1+\gamma ^{2}&\gamma &0\\\gamma &1&0\\0&0&1\end{bmatrix}}}
Therefore,
B
−
1
=
[
1
−
γ
0
−
γ
1
+
γ
2
0
0
0
1
]
{\displaystyle {\boldsymbol {B}}^{-1}={\begin{bmatrix}1&-\gamma &0\\-\gamma &1+\gamma ^{2}&0\\0&0&1\end{bmatrix}}}
The Cauchy stress is given by
σ
=
[
−
p
∗
+
2
(
C
1
−
C
2
)
+
2
C
1
γ
2
2
(
C
1
+
C
2
)
γ
0
2
(
C
1
+
C
2
)
γ
−
p
∗
+
2
(
C
1
−
C
2
)
−
2
C
2
γ
2
0
0
0
−
p
∗
+
2
(
C
1
−
C
2
)
]
{\displaystyle {\boldsymbol {\sigma }}={\begin{bmatrix}-p^{*}+2(C_{1}-C_{2})+2C_{1}\gamma ^{2}&2(C_{1}+C_{2})\gamma &0\\2(C_{1}+C_{2})\gamma &-p^{*}+2(C_{1}-C_{2})-2C_{2}\gamma ^{2}&0\\0&0&-p^{*}+2(C_{1}-C_{2})\end{bmatrix}}}
For consistency with linear elasticity, clearly
μ
=
2
(
C
1
+
C
2
)
{\displaystyle \mu =2(C_{1}+C_{2})}
μ
{\displaystyle \mu }
Rubber
Elastic response of rubber-like materials are often modeled based on the Mooney–Rivlin model. The constants
C
1
,
C
2
{\displaystyle C_{1},C_{2}}
[ 8]
Notes and references
^ Mooney, M., 1940, A theory of large elastic deformation , Journal of Applied Physics, 11(9), pp. 582–592.
^ Rivlin, R. S., 1948, Large elastic deformations of isotropic materials. IV. Further developments of the general theory , Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences, 241(835), pp. 379–397.
^ Boulanger, P. and Hayes, M. A., 2001, "Finite amplitude waves in Mooney–Rivlin and Hadamard materials", in Topics in Finite Elasticity , ed. M. A Hayes and G. Soccomandi, International Center for Mechanical Sciences.
^ C. W. Macosko, 1994, Rheology: principles, measurement and applications , VCH Publishers, ISBN 1-56081-579-5 .
^ Unimodularity in this context means
det
B
¯
=
1
{\displaystyle \det {\bar {\boldsymbol {B}}}=1}
^ Bower, Allan (2009). Applied Mechanics of Solids ISBN 978-1-4398-0247-2 . Retrieved 2018-04-19 . ^ a b Ogden, R. W., 1984, Nonlinear elastic deformations , Dover
^ Hamza, Muhsin; Alwan, Hassan (2010). "Hyperelastic Constitutive Modeling of Rubber and Rubber-Like Materials under Finite Strain" . Engineering and Technology Journal . 28 (13): 2560– 2575. doi :10.30684/etj.28.13.5
See also