Differentiation rules

Part of a series of articles about
Calculus
${\displaystyle \int _{a}^{b}f'(t)\,dt=f(b)-f(a)}$
Fundamental theorem Limits Continuity Rolle's theorem Mean value theorem Inverse function theorem
Differential Definitions Derivative (generalizations) Differential infinitesimal of a function total Concepts Differentiation notation Second derivative Implicit differentiation Logarithmic differentiation Related rates Taylor's theorem Sum Product Chain Power Quotient L'Hôpital's rule Inverse General Leibniz Faà di Bruno's formula Reynolds
Integral Lists of integrals Integral transform Leibniz integral rule Definitions Antiderivative Integral (improper) Riemann integral Lebesgue integration Contour integration Integral of inverse functions Integration by Parts Discs Cylindrical shells Substitution (trigonometric, tangent half-angle, Euler) Euler's formula Partial fractions (Heaviside's method) Changing order Reduction formulae Differentiating under the integral sign Risch algorithm
Series Geometric (arithmetico-geometric) Harmonic Alternating Power Binomial Taylor Convergence tests Summand limit (term test) Ratio Root Integral Direct comparison Limit comparison Alternating series Cauchy condensation Dirichlet Abel
Vector Gradient Divergence Curl Laplacian Directional derivative Identities Theorems Gradient Green's Stokes' Divergence Generalized Stokes Helmholtz decomposition
Multivariable Formalisms Matrix Tensor Exterior Geometric Definitions Partial derivative Multiple integral Line integral Surface integral Volume integral Jacobian Hessian
Advanced Calculus on Euclidean space Generalized functions Limit of distributions
Specialized Fractional Malliavin Stochastic Variations
Miscellanea Precalculus History Glossary List of topics Integration Bee Mathematical analysis Nonstandard analysis

This article is a summary of differentiation rules, that is, rules for computing the derivative of a function in calculus.

Unless otherwise stated, all functions are functions of real numbers (${\textstyle \mathbb {R} }$) that return real values, although, more generally, the formulas below apply wherever they are well defined,^[1][2] including the case of complex numbers (${\textstyle \mathbb {C} }$).^[3]

For any value of ${\textstyle c}$, where ${\textstyle c\in \mathbb {R} }$, if ${\textstyle f(x)}$ is the constant function given by ${\textstyle f(x)=c}$, then ${\textstyle {\frac {df}{dx}}=0}$.^[4]

Let ${\textstyle c\in \mathbb {R} }$ and ${\textstyle f(x)=c}$. By the definition of the derivative: $${\displaystyle {\begin{aligned}f'(x)&=\lim _{h\to 0}{\frac {f(x+h)-f(x)}{h}}\\&=\lim _{h\to 0}{\frac {(c)-(c)}{h}}\\&=\lim _{h\to 0}{\frac {0}{h}}\\&=\lim _{h\to 0}0\\&=0.\end{aligned}}}$$

This computation shows that the derivative of any constant function is 0.

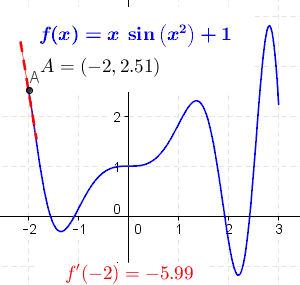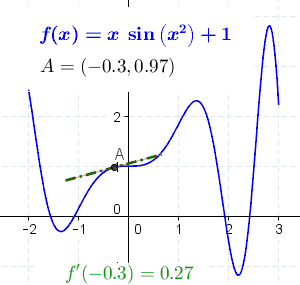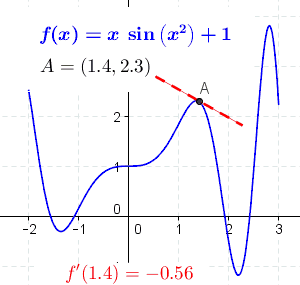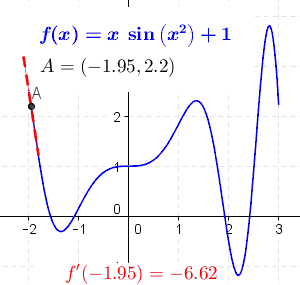
The derivative of the function at a point is the slope of the line tangent to the curve at the point. The slope of the constant function is 0, because the tangent line to the constant function is horizontal and its angle is 0.

In other words, the value of the constant function, ${\textstyle y}$, will not change as the value of ${\textstyle x}$ increases or decreases.

For any functions ${\textstyle f}$ and ${\textstyle g}$ and any real numbers ${\textstyle a}$ and ${\textstyle b}$, the derivative of the function ${\textstyle h(x)=af(x)+bg(x)}$ with respect to ${\textstyle x}$ is ${\textstyle h'(x)=af'(x)+bg'(x)}$.

In Leibniz's notation, this formula is written as: $${\displaystyle {\frac {d(af+bg)}{dx}}=a{\frac {df}{dx}}+b{\frac {dg}{dx}}.}$$

Special cases include:

• The constant factor rule:

$${\displaystyle (af)'=af',}$$

• The sum rule:

$${\displaystyle (f+g)'=f'+g',}$$

• The difference rule:

$${\displaystyle (f-g)'=f'-g'.}$$

For the functions ${\textstyle f}$ and ${\textstyle g}$, the derivative of the function ${\textstyle h(x)=f(x)g(x)}$ with respect to ${\textstyle x}$ is: $${\displaystyle h'(x)=(fg)'(x)=f'(x)g(x)+f(x)g'(x).}$$

In Leibniz's notation, this formula is written: $${\displaystyle {\frac {d(fg)}{dx}}=g{\frac {df}{dx}}+f{\frac {dg}{dx}}.}$$

The derivative of the function ${\textstyle h(x)=f(g(x))}$ is: $${\displaystyle h'(x)=f'(g(x))\cdot g'(x).}$$

In Leibniz's notation, this formula is written as: $${\displaystyle {\frac {d}{dx}}h(x)=\left.{\frac {d}{dz}}f(z)\right|_{z=g(x)}\cdot {\frac {d}{dx}}g(x),}$$ often abridged to: $${\displaystyle {\frac {dh(x)}{dx}}={\frac {df(g(x))}{dg(x)}}\cdot {\frac {dg(x)}{dx}}.}$$

Focusing on the notion of maps, and the differential being a map ${\textstyle {\text{D}}}$, this formula is written in a more concise way as: $${\displaystyle [{\text{D}}(f\circ g)]_{x}=[{\text{D}}f]_{g(x)}\cdot [{\text{D}}g]_{x}.}$$

If the function ${\textstyle f}$ has an inverse function ${\textstyle g}$, meaning that ${\textstyle g(f(x))=x}$ and ${\textstyle f(g(y))=y}$, then: $${\displaystyle g'={\frac {1}{f'\circ g}}.}$$

In Leibniz notation, this formula is written as: $${\displaystyle {\frac {dx}{dy}}={\frac {1}{\frac {dy}{dx}}}.}$$

If ${\textstyle f(x)=x^{r}}$, for any real number ${\textstyle r\neq 0}$, then: $${\displaystyle f'(x)=rx^{r-1}.}$$

When ${\textstyle r=1}$, this formula becomes the special case that, if ${\textstyle f(x)=x}$, then ${\textstyle f'(x)=1}$.

Combining the power rule with the sum and constant multiple rules permits the computation of the derivative of any polynomial.

The derivative of ${\textstyle h(x)={\frac {1}{f(x)}}}$ for any (nonvanishing) function ${\textstyle f}$ is: $${\displaystyle h'(x)=-{\frac {f'(x)}{(f(x))^{2}}},}$$ wherever ${\textstyle f}$ is nonzero.

In Leibniz's notation, this formula is written: $${\displaystyle {\frac {d\left({\frac {1}{f}}\right)}{dx}}=-{\frac {1}{f^{2}}}{\frac {df}{dx}}.}$$

The reciprocal rule can be derived either from the quotient rule or from the combination of power rule and chain rule.

If ${\textstyle f}$ and ${\textstyle g}$ are functions, then: $${\displaystyle \left({\frac {f}{g}}\right)'={\frac {f'g-g'f}{g^{2}}},}$$ wherever ${\textstyle g}$ is nonzero.

This can be derived from the product rule and the reciprocal rule.

The elementary power rule generalizes considerably. The most general power rule is the functional power rule: for any functions ${\textstyle f}$ and ${\textstyle g}$, $${\displaystyle (f^{g})'=\left(e^{g\ln f}\right)'=f^{g}\left(f'{g \over f}+g'\ln f\right),\quad }$$ wherever both sides are well defined.

Special cases:

• If ${\textstyle f(x)=x^{a}}$, then ${\textstyle f'(x)=ax^{a-1}}$ when ${\textstyle a}$ is any nonzero real number and ${\textstyle x}$ is positive.
• The reciprocal rule may be derived as the special case where ${\textstyle g(x)=-1\!}$.

$${\displaystyle {\frac {d}{dx}}\left(c^{ax}\right)={ac^{ax}\ln c},\qquad c>0.}$$ The equation above is true for all ${\displaystyle c}$, but the derivative for ${\displaystyle c<0}$ yields a complex number.

$${\displaystyle {\frac {d}{dx}}\left(e^{ax}\right)=ae^{ax}.}$$

$${\displaystyle {\frac {d}{dx}}\left(\log _{c}x\right)={1 \over x\ln c},\qquad c>1.}$$ The equation above is also true for all ${\textstyle c}$ but yields a complex number if ${\textstyle c<0}$.

$${\displaystyle {\frac {d}{dx}}\left(\ln x\right)={1 \over x},\qquad x>0.}$$

$${\displaystyle {\frac {d}{dx}}\left(\ln |x|\right)={1 \over x},\qquad x\neq 0.}$$

$${\displaystyle {\frac {d}{dx}}\left(W(x)\right)={1 \over {x+e^{W(x)}}},\qquad x>-{1 \over e},}$$ where ${\textstyle W(x)}$ is the Lambert W function.

$${\displaystyle {\frac {d}{dx}}\left(x^{x}\right)=x^{x}(1+\ln x).}$$

$${\displaystyle {\frac {d}{dx}}\left(f(x)^{g(x)}\right)=g(x)f(x)^{g(x)-1}{\frac {df}{dx}}+f(x)^{g(x)}\ln {(f(x))}{\frac {dg}{dx}},\qquad {\text{if }}f(x)>0{\text{ and }}{\frac {df}{dx}}{\text{ and }}{\frac {dg}{dx}}{\text{ exist.}}}$$

$${\displaystyle {\frac {d}{dx}}\left(f_{1}(x)^{f_{2}(x)^{\left(...\right)^{f_{n}(x)}}}\right)=\left[\sum \limits _{k=1}^{n}{\frac {\partial }{\partial x_{k}}}\left(f_{1}(x_{1})^{f_{2}(x_{2})^{\left(...\right)^{f_{n}(x_{n})}}}\right)\right]{\biggr \vert }_{x_{1}=x_{2}=...=x_{n}=x},\qquad {\text{ if }}f_{i<n}(x)>0{\text{ and }}{\frac {df_{i}}{dx}}{\text{ exists.}}}$$

The logarithmic derivative is another way of stating the rule for differentiating the logarithm of a function (using the chain rule): $${\displaystyle (\ln f)'={\frac {f'}{f}},}$$ wherever ${\textstyle f}$ is positive.

Logarithmic differentiation is a technique which uses logarithms and its differentiation rules to simplify certain expressions before actually applying the derivative.

Logarithms can be used to remove exponents, convert products into sums, and convert division into subtraction—each of which may lead to a simplified expression for taking derivatives.

${\displaystyle {\frac {d}{dx}}\sin x=\cos x}$	${\displaystyle {\frac {d}{dx}}\arcsin x={\frac {1}{\sqrt {1-x^{2}}}}}$
${\displaystyle {\frac {d}{dx}}\cos x=-\sin x}$	${\displaystyle {\frac {d}{dx}}\arccos x=-{\frac {1}{\sqrt {1-x^{2}}}}}$
${\displaystyle {\frac {d}{dx}}\tan x=\sec ^{2}x={\frac {1}{\cos ^{2}x}}=1+\tan ^{2}x}$	${\displaystyle {\frac {d}{dx}}\arctan x={\frac {1}{1+x^{2}}}}$
${\displaystyle {\frac {d}{dx}}\csc x=-\csc {x}\cot {x}}$	${\displaystyle {\frac {d}{dx}}\operatorname {arccsc} x=-{\frac {1}{|x|{\sqrt {x^{2}-1}}}}}$
${\displaystyle {\frac {d}{dx}}\sec x=\sec {x}\tan {x}}$	${\displaystyle {\frac {d}{dx}}\operatorname {arcsec} x={\frac {1}{|x|{\sqrt {x^{2}-1}}}}}$
${\displaystyle {\frac {d}{dx}}\cot x=-\csc ^{2}x=-{\frac {1}{\sin ^{2}x}}=-1-\cot ^{2}x}$	${\displaystyle {\frac {d}{dx}}\operatorname {arccot} x=-{1 \over 1+x^{2}}}$

The derivatives in the table above are for when the range of the inverse secant is ${\textstyle [0,\pi ]}$ and when the range of the inverse cosecant is ${\textstyle \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}$.

It is common to additionally define an inverse tangent function with two arguments, ${\textstyle \arctan(y,x)}$. Its value lies in the range ${\textstyle [-\pi ,\pi ]}$ and reflects the quadrant of the point ${\textstyle (x,y)}$. For the first and fourth quadrant (i.e., ${\displaystyle x>0}$), one has ${\textstyle \arctan(y,x>0)=\arctan({\frac {y}{x}})}$. Its partial derivatives are: $${\displaystyle {\frac {\partial \arctan(y,x)}{\partial y}}={\frac {x}{x^{2}+y^{2}}}\qquad {\text{and}}\qquad {\frac {\partial \arctan(y,x)}{\partial x}}={\frac {-y}{x^{2}+y^{2}}}.}$$

${\displaystyle {\frac {d}{dx}}\sinh x=\cosh x}$	${\displaystyle {\frac {d}{dx}}\operatorname {arsinh} x={\frac {1}{\sqrt {1+x^{2}}}}}$
${\displaystyle {\frac {d}{dx}}\cosh x=\sinh x}$	${\displaystyle {\frac {d}{dx}}\operatorname {arcosh} x={\frac {1}{\sqrt {x^{2}-1}}}}$
${\displaystyle {\frac {d}{dx}}\tanh x={\operatorname {sech} ^{2}x}=1-\tanh ^{2}x}$	${\displaystyle {\frac {d}{dx}}\operatorname {artanh} x={\frac {1}{1-x^{2}}}}$
${\displaystyle {\frac {d}{dx}}\operatorname {csch} x=-\operatorname {csch} {x}\coth {x}}$	${\displaystyle {\frac {d}{dx}}\operatorname {arcsch} x=-{\frac {1}{|x|{\sqrt {1+x^{2}}}}}}$
${\displaystyle {\frac {d}{dx}}\operatorname {sech} x=-\operatorname {sech} {x}\tanh {x}}$	${\displaystyle {\frac {d}{dx}}\operatorname {arsech} x=-{\frac {1}{x{\sqrt {1-x^{2}}}}}}$
${\displaystyle {\frac {d}{dx}}\coth x=-\operatorname {csch} ^{2}x=1-\coth ^{2}x}$	${\displaystyle {\frac {d}{dx}}\operatorname {arcoth} x={\frac {1}{1-x^{2}}}}$

$${\displaystyle \Gamma (x)=\int _{0}^{\infty }t^{x-1}e^{-t}\,dt}$$ $${\displaystyle {\begin{aligned}\Gamma '(x)&=\int _{0}^{\infty }t^{x-1}e^{-t}\ln t\,dt\\&=\Gamma (x)\left(\sum _{n=1}^{\infty }\left(\ln \left(1+{\dfrac {1}{n}}\right)-{\dfrac {1}{x+n}}\right)-{\dfrac {1}{x}}\right)\\&=\Gamma (x)\psi (x),\end{aligned}}}$$ with ${\textstyle \psi (x)}$ being the digamma function, expressed by the parenthesized expression to the right of ${\textstyle \Gamma (x)}$ in the line above.

$${\displaystyle \zeta (x)=\sum _{n=1}^{\infty }{\frac {1}{n^{x}}}}$$ $${\displaystyle {\begin{aligned}\zeta '(x)&=-\sum _{n=1}^{\infty }{\frac {\ln n}{n^{x}}}=-{\frac {\ln 2}{2^{x}}}-{\frac {\ln 3}{3^{x}}}-{\frac {\ln 4}{4^{x}}}-\cdots \\&=-\sum _{p{\text{ prime}}}{\frac {p^{-x}\ln p}{(1-p^{-x})^{2}}}\prod _{q{\text{ prime}},q\neq p}{\frac {1}{1-q^{-x}}}\end{aligned}}}$$

Suppose that it is required to differentiate with respect to ${\textstyle x}$ the function: $${\displaystyle F(x)=\int _{a(x)}^{b(x)}f(x,t)\,dt,}$$

where the functions ${\textstyle f(x,t)}$ and ${\textstyle {\frac {\partial }{\partial x}}\,f(x,t)}$ are both continuous in both ${\textstyle t}$ and ${\textstyle x}$ in some region of the ${\textstyle (t,x)}$ plane, including ${\textstyle a(x)\leq t\leq b(x)}$, where ${\textstyle x_{0}\leq x\leq x_{1}}$, and the functions ${\textstyle a(x)}$ and ${\textstyle b(x)}$ are both continuous and both have continuous derivatives for ${\textstyle x_{0}\leq x\leq x_{1}}$. Then, for ${\textstyle \,x_{0}\leq x\leq x_{1}}$: $${\displaystyle F'(x)=f(x,b(x))\,b'(x)-f(x,a(x))\,a'(x)+\int _{a(x)}^{b(x)}{\frac {\partial }{\partial x}}\,f(x,t)\;dt\,.}$$

This formula is the general form of the Leibniz integral rule and can be derived using the fundamental theorem of calculus.

Some rules exist for computing the ${\textstyle n}$th derivative of functions, where ${\textstyle n}$ is a positive integer, including:

If ${\textstyle f}$ and ${\textstyle g}$ are ${\textstyle n}$-times differentiable, then: $${\displaystyle {\frac {d^{n}}{dx^{n}}}[f(g(x))]=n!\sum _{\{k_{m}\}}f^{(r)}(g(x))\prod _{m=1}^{n}{\frac {1}{k_{m}!}}\left(g^{(m)}(x)\right)^{k_{m}},}$$ where ${\textstyle r=\sum _{m=1}^{n-1}k_{m}}$ and the set ${\textstyle \{k_{m}\}}$ consists of all non-negative integer solutions of the Diophantine equation ${\textstyle \sum _{m=1}^{n}mk_{m}=n}$.

If ${\textstyle f}$ and ${\textstyle g}$ are ${\textstyle n}$-times differentiable, then: $${\displaystyle {\frac {d^{n}}{dx^{n}}}[f(x)g(x)]=\sum _{k=0}^{n}{\binom {n}{k}}{\frac {d^{n-k}}{dx^{n-k}}}f(x){\frac {d^{k}}{dx^{k}}}g(x).}$$

• Differentiable function – Mathematical function whose derivative exists
• Differential of a function – Notion in calculus
• Differentiation of integrals – Problem in mathematics
• Differentiation under the integral sign – Differentiation under the integral sign formulaPages displaying short descriptions of redirect targets
• Hyperbolic functions – Collective name of 6 mathematical functions
• Inverse hyperbolic functions – Mathematical functions
• Inverse trigonometric functions – Inverse functions of sin, cos, tan, etc.
• Lists of integrals
• List of mathematical functions
• Matrix calculus – Specialized notation for multivariable calculus
• Trigonometric functions – Functions of an angle
• Vector calculus identities – Mathematical identities

These rules are given in many books, both on elementary and advanced calculus, in pure and applied mathematics. Those in this article (in addition to the above references) can be found in:

• Mathematical Handbook of Formulas and Tables (3rd edition), S. Lipschutz, M.R. Spiegel, J. Liu, Schaum's Outline Series, 2009, ISBN 978-0-07-154855-7.
• The Cambridge Handbook of Physics Formulas, G. Woan, Cambridge University Press, 2010, ISBN 978-0-521-57507-2.
• Mathematical methods for physics and engineering, K.F. Riley, M.P. Hobson, S.J. Bence, Cambridge University Press, 2010, ISBN 978-0-521-86153-3
• NIST Handbook of Mathematical Functions, F. W. J. Olver, D. W. Lozier, R. F. Boisvert, C. W. Clark, Cambridge University Press, 2010, ISBN 978-0-521-19225-5.

• Derivative calculator with formula simplification
• The table of derivatives with animated proves