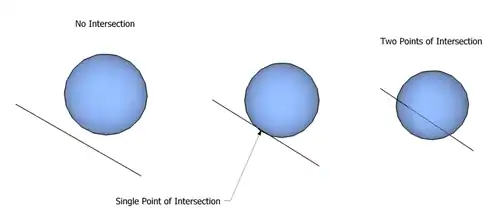
The three possible line-sphere intersections: In analytic geometry , a line and a sphere can intersect in three ways:
No intersection at all
Intersection in exactly one point
Intersection in two points. Methods for distinguishing these cases, and determining the coordinates for the points in the latter cases, are useful in a number of circumstances. For example, it is a common calculation to perform during ray tracing .[ 1]
Calculation using vectors in 3D
In vector notation , the equations are as follows:
Equation for a sphere
‖
x
−
c
‖
2
=
r
2
{\displaystyle \left\Vert \mathbf {x} -\mathbf {c} \right\Vert ^{2}=r^{2}}
x
{\displaystyle \mathbf {x} }
c
{\displaystyle \mathbf {c} }
r
{\displaystyle r}
Equation for a line starting at
o
{\displaystyle \mathbf {o} }
x
=
o
+
d
u
{\displaystyle \mathbf {x} =\mathbf {o} +d\mathbf {u} }
x
{\displaystyle \mathbf {x} }
o
{\displaystyle \mathbf {o} }
d
{\displaystyle d}
u
{\displaystyle \mathbf {u} }
Searching for points that are on the line and on the sphere means combining the equations and solving for
d
{\displaystyle d}
dot product of vectors:
Equations combined
‖
o
+
d
u
−
c
‖
2
=
r
2
⇔
(
o
+
d
u
−
c
)
⋅
(
o
+
d
u
−
c
)
=
r
2
{\displaystyle \left\Vert \mathbf {o} +d\mathbf {u} -\mathbf {c} \right\Vert ^{2}=r^{2}\Leftrightarrow (\mathbf {o} +d\mathbf {u} -\mathbf {c} )\cdot (\mathbf {o} +d\mathbf {u} -\mathbf {c} )=r^{2}}
Expanded and rearranged:
d
2
(
u
⋅
u
)
+
2
d
[
u
⋅
(
o
−
c
)
]
+
(
o
−
c
)
⋅
(
o
−
c
)
−
r
2
=
0
{\displaystyle d^{2}(\mathbf {u} \cdot \mathbf {u} )+2d[\mathbf {u} \cdot (\mathbf {o} -\mathbf {c} )]+(\mathbf {o} -\mathbf {c} )\cdot (\mathbf {o} -\mathbf {c} )-r^{2}=0}
The form of a quadratic formula is now observable. (This quadratic equation is an instance of Joachimsthal's equation.[ 2]
a
d
2
+
b
d
+
c
=
0
{\displaystyle ad^{2}+bd+c=0}
where
a
=
u
⋅
u
=
‖
u
‖
2
{\displaystyle a=\mathbf {u} \cdot \mathbf {u} =\left\Vert \mathbf {u} \right\Vert ^{2}}
b
=
2
[
u
⋅
(
o
−
c
)
]
{\displaystyle b=2[\mathbf {u} \cdot (\mathbf {o} -\mathbf {c} )]}
c
=
(
o
−
c
)
⋅
(
o
−
c
)
−
r
2
=
‖
o
−
c
‖
2
−
r
2
{\displaystyle c=(\mathbf {o} -\mathbf {c} )\cdot (\mathbf {o} -\mathbf {c} )-r^{2}=\left\Vert \mathbf {o} -\mathbf {c} \right\Vert ^{2}-r^{2}}
Simplified
d
=
−
2
[
u
⋅
(
o
−
c
)
]
±
(
2
[
u
⋅
(
o
−
c
)
]
)
2
−
4
‖
u
‖
2
(
‖
o
−
c
‖
2
−
r
2
)
2
‖
u
‖
2
{\displaystyle d={\frac {-2[\mathbf {u} \cdot (\mathbf {o} -\mathbf {c} )]\pm {\sqrt {(2[\mathbf {u} \cdot (\mathbf {o} -\mathbf {c} )])^{2}-4\left\Vert \mathbf {u} \right\Vert ^{2}(\left\Vert \mathbf {o} -\mathbf {c} \right\Vert ^{2}-r^{2})}}}{2\left\Vert \mathbf {u} \right\Vert ^{2}}}}
Note that in the specific case where
u
{\displaystyle \mathbf {u} }
‖
u
‖
2
=
1
{\displaystyle \left\Vert \mathbf {u} \right\Vert ^{2}=1}
u
^
{\displaystyle {\hat {\mathbf {u} }}}
u
{\displaystyle \mathbf {u} }
∇
=
[
u
^
⋅
(
o
−
c
)
]
2
−
(
‖
o
−
c
‖
2
−
r
2
)
{\displaystyle \nabla =[{\hat {\mathbf {u} }}\cdot (\mathbf {o} -\mathbf {c} )]^{2}-(\left\Vert \mathbf {o} -\mathbf {c} \right\Vert ^{2}-r^{2})}
d
=
−
[
u
^
⋅
(
o
−
c
)
]
±
∇
{\displaystyle d=-[{\hat {\mathbf {u} }}\cdot (\mathbf {o} -\mathbf {c} )]\pm {\sqrt {\nabla }}}
If
∇
<
0
{\displaystyle \nabla <0}
If
∇
=
0
{\displaystyle \nabla =0}
If
∇
>
0
{\displaystyle \nabla >0}
See also
References
^ Eberly, David H. (2006). 3D game engine design: a practical approach to real-time computer graphics, 2nd edition . Morgan Kaufmann. p. 698. ISBN 0-12-229063-1 . ^ "Joachimsthal's Equation" .