Kaniadakis Gamma distribution

κ-Gamma distribution
Probability density function
Parameters	${\displaystyle 0\leq \kappa <1}$ ${\displaystyle \alpha >0}$ shape (real) ${\displaystyle \beta >0}$ rate (real) ${\displaystyle 0<\nu <1/\kappa }$
Support	${\displaystyle x\in [0,+\infty )}$
PDF	${\displaystyle (1+\kappa \nu )(2\kappa )^{\nu }{\frac {\Gamma {\big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}{\big )}}{\Gamma {\big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}{\big )}}}{\frac {\alpha \beta ^{\nu }}{\Gamma {\big (}\nu {\big )}}}x^{\alpha \nu -1}\exp _{\kappa }(-\beta x^{\alpha })}$
CDF	${\displaystyle (1+\kappa \nu )(2\kappa )^{\nu }{\frac {\Gamma {\big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}{\big )}}{\Gamma {\big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}{\big )}}}{\frac {\alpha \beta ^{\nu }}{\Gamma {\big (}\nu {\big )}}}\int _{0}^{x}z^{\alpha \nu -1}\exp _{\kappa }(-\beta z^{\alpha })dz}$
Mode	${\displaystyle \beta ^{-1/\alpha }{\Bigg (}\nu -{\frac {1}{\alpha }}{\Bigg )}^{\frac {1}{\alpha }}{\Bigg [}1-\kappa ^{2}{\bigg (}\nu -{\frac {1}{\alpha }}{\bigg )}^{2}{\Bigg ]}^{-{\frac {1}{2\alpha }}}}$
Method of moments	${\displaystyle \beta ^{-m/\alpha }{\frac {(1+\kappa \nu )(2\kappa )^{-m/\alpha }}{1+\kappa {\big (}\nu +{\frac {m}{\alpha }}{\big )}}}{\frac {\Gamma {\big (}\nu +{\frac {m}{\alpha }}{\big )}}{\Gamma (\nu )}}{\frac {\Gamma {\Big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}{\Big )}}{\Gamma {\Big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}{\Big )}}}{\frac {\Gamma {\Big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}-{\frac {m}{2\alpha }}{\Big )}}{\Gamma {\Big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}+{\frac {m}{2\alpha }}{\Big )}}}}$

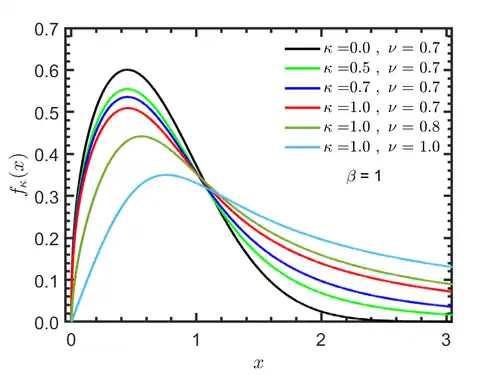
The Kaniadakis Generalized Gamma distribution (or κ-Generalized Gamma distribution) is a four-parameter family of continuous statistical distributions, supported on a semi-infinite interval [0,∞), which arising from the Kaniadakis statistics. It is one example of a Kaniadakis distribution. The κ-Gamma is a deformation of the Generalized Gamma distribution.

The Kaniadakis κ-Gamma distribution has the following probability density function:^[1]

${\displaystyle f_{_{\kappa }}(x)=(1+\kappa \nu )(2\kappa )^{\nu }{\frac {\Gamma {\big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}{\big )}}{\Gamma {\big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}{\big )}}}{\frac {\alpha \beta ^{\nu }}{\Gamma {\big (}\nu {\big )}}}x^{\alpha \nu -1}\exp _{\kappa }(-\beta x^{\alpha })}$

valid for ${\displaystyle x\geq 0}$, where ${\displaystyle 0\leq |\kappa |<1}$ is the entropic index associated with the Kaniadakis entropy, ${\displaystyle 0<\nu <1/\kappa }$, ${\displaystyle \beta >0}$ is the scale parameter, and ${\displaystyle \alpha >0}$ is the shape parameter.

The ordinary generalized Gamma distribution is recovered as ${\displaystyle \kappa \rightarrow 0}$: ${\displaystyle f_{_{0}}(x)={\frac {|\alpha |\beta ^{\nu }}{\Gamma \left(\nu \right)}}x^{\alpha \nu -1}\exp _{\kappa }(-\beta x^{\alpha })}$.

The cumulative distribution function of κ-Gamma distribution assumes the form:

${\displaystyle F_{\kappa }(x)=(1+\kappa \nu )(2\kappa )^{\nu }{\frac {\Gamma {\big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}{\big )}}{\Gamma {\big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}{\big )}}}{\frac {\alpha \beta ^{\nu }}{\Gamma {\big (}\nu {\big )}}}\int _{0}^{x}z^{\alpha \nu -1}\exp _{\kappa }(-\beta z^{\alpha })dz}$

valid for ${\displaystyle x\geq 0}$, where ${\displaystyle 0\leq |\kappa |<1}$. The cumulative Generalized Gamma distribution is recovered in the classical limit ${\displaystyle \kappa \rightarrow 0}$.

The κ-Gamma distribution has moment of order ${\displaystyle m}$ given by^[1]

${\displaystyle \operatorname {E} [X^{m}]=\beta ^{-m/\alpha }{\frac {(1+\kappa \nu )(2\kappa )^{-m/\alpha }}{1+\kappa {\big (}\nu +{\frac {m}{\alpha }}{\big )}}}{\frac {\Gamma {\big (}\nu +{\frac {m}{\alpha }}{\big )}}{\Gamma (\nu )}}{\frac {\Gamma {\Big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}{\Big )}}{\Gamma {\Big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}{\Big )}}}{\frac {\Gamma {\Big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}-{\frac {m}{2\alpha }}{\Big )}}{\Gamma {\Big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}+{\frac {m}{2\alpha }}{\Big )}}}}$

The moment of order ${\displaystyle m}$ of the κ-Gamma distribution is finite for ${\displaystyle 0<\nu +m/\alpha <1/\kappa }$.

The mode is given by:

${\displaystyle x_{\textrm {mode}}=\beta ^{-1/\alpha }{\Bigg (}\nu -{\frac {1}{\alpha }}{\Bigg )}^{\frac {1}{\alpha }}{\Bigg [}1-\kappa ^{2}{\bigg (}\nu -{\frac {1}{\alpha }}{\bigg )}^{2}{\Bigg ]}^{-{\frac {1}{2\alpha }}}}$

The κ-Gamma distribution behaves asymptotically as follows:^[1]

${\displaystyle \lim _{x\to +\infty }f_{\kappa }(x)\sim (2\kappa \beta )^{-1/\kappa }(1+\kappa \nu )(2\kappa )^{\nu }{\frac {\Gamma {\big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}{\big )}}{\Gamma {\big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}{\big )}}}{\frac {\alpha \beta ^{\nu }}{\Gamma {\big (}\nu {\big )}}}x^{\alpha \nu -1-\alpha /\kappa }}$

${\displaystyle \lim _{x\to 0^{+}}f_{\kappa }(x)=(1+\kappa \nu )(2\kappa )^{\nu }{\frac {\Gamma {\big (}{\frac {1}{2\kappa }}+{\frac {\nu }{2}}{\big )}}{\Gamma {\big (}{\frac {1}{2\kappa }}-{\frac {\nu }{2}}{\big )}}}{\frac {\alpha \beta ^{\nu }}{\Gamma {\big (}\nu {\big )}}}x^{\alpha \nu -1}}$

• The κ-Gamma distributions is a generalization of:
  • κ-Exponential distribution of type I, when ${\displaystyle \alpha =\nu =1}$;
  • Kaniadakis κ-Erlang distribution, when ${\displaystyle \alpha =1}$ and ${\displaystyle \nu =n=}$ positive integer.
  • κ-Half-Normal distribution, when ${\displaystyle \alpha =2}$ and ${\displaystyle \nu =1/2}$;
• A κ-Gamma distribution corresponds to several probability distributions when ${\displaystyle \kappa =0}$, such as:
  • Gamma distribution, when ${\displaystyle \alpha =1}$;
  • Exponential distribution, when ${\displaystyle \alpha =\nu =1}$;
  • Erlang distribution, when ${\displaystyle \alpha =1}$ and ${\displaystyle \nu =n=}$ positive integer;
  • Chi-Squared distribution, when ${\displaystyle \alpha =1}$ and ${\displaystyle \nu =}$ half integer;
  • Nakagami distribution, when ${\displaystyle \alpha =2}$ and ${\displaystyle \nu >0}$;
  • Rayleigh distribution, when ${\displaystyle \alpha =2}$ and ${\displaystyle \nu =1}$;
  • Chi distribution, when ${\displaystyle \alpha =2}$ and ${\displaystyle \nu =}$ half integer;
  • Maxwell distribution, when ${\displaystyle \alpha =2}$ and ${\displaystyle \nu =3/2}$;
  • Half-Normal distribution, when ${\displaystyle \alpha =2}$ and ${\displaystyle \nu =1/2}$;
  • Weibull distribution, when ${\displaystyle \alpha >0}$ and ${\displaystyle \nu =1}$;
  • Stretched Exponential distribution, when ${\displaystyle \alpha >0}$ and ${\displaystyle \nu =1/\alpha }$;

• Giorgio Kaniadakis
• Kaniadakis statistics
• Kaniadakis distribution
• Kaniadakis κ-Exponential distribution
• Kaniadakis κ-Gaussian distribution
• Kaniadakis κ-Weibull distribution
• Kaniadakis κ-Logistic distribution
• Kaniadakis κ-Erlang distribution

• Kaniadakis Statistics on arXiv.org