Dawson function

In mathematics, the Dawson function or Dawson integral^[1] (named after H. G. Dawson^[2]) is the one-sided Fourier–Laplace sine transform of the Gaussian function.

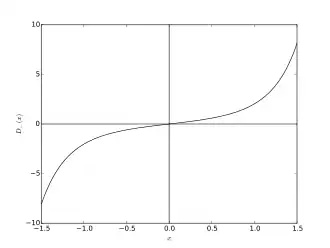
The Dawson function is defined as either: $${\displaystyle D_{+}(x)=e^{-x^{2}}\int _{0}^{x}e^{t^{2}}\,dt,}$$ also denoted as ${\displaystyle F(x)}$ or ${\displaystyle D(x),}$ or alternatively $${\displaystyle D_{-}(x)=e^{x^{2}}\int _{0}^{x}e^{-t^{2}}\,dt.\!}$$

The Dawson function is the one-sided Fourier–Laplace sine transform of the Gaussian function, $${\displaystyle D_{+}(x)={\frac {1}{2}}\int _{0}^{\infty }e^{-t^{2}/4}\,\sin(xt)\,dt.}$$

It is closely related to the error function erf, as

${\displaystyle D_{+}(x)={{\sqrt {\pi }} \over 2}e^{-x^{2}}\operatorname {erfi} (x)=-{i{\sqrt {\pi }} \over 2}e^{-x^{2}}\operatorname {erf} (ix)}$

where erfi is the imaginary error function, erfi(x) = −i erf(ix).
Similarly, $${\displaystyle D_{-}(x)={\frac {\sqrt {\pi }}{2}}e^{x^{2}}\operatorname {erf} (x)}$$ in terms of the real error function, erf.

In terms of either erfi or the Faddeeva function ${\displaystyle w(z),}$ the Dawson function can be extended to the entire complex plane:^[3] $${\displaystyle F(z)={{\sqrt {\pi }} \over 2}e^{-z^{2}}\operatorname {erfi} (z)={\frac {i{\sqrt {\pi }}}{2}}\left[e^{-z^{2}}-w(z)\right],}$$ which simplifies to $${\displaystyle D_{+}(x)=F(x)={\frac {\sqrt {\pi }}{2}}\operatorname {Im} [w(x)]}$$ $${\displaystyle D_{-}(x)=iF(-ix)=-{\frac {\sqrt {\pi }}{2}}\left[e^{x^{2}}-w(-ix)\right]}$$ for real ${\displaystyle x.}$

For ${\displaystyle |x|}$ near zero, F(x) ≈ x. For ${\displaystyle |x|}$ large, F(x) ≈ 1/(2x). More specifically, near the origin it has the series expansion $${\displaystyle F(x)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}\,2^{k}}{(2k+1)!!}}\,x^{2k+1}=x-{\frac {2}{3}}x^{3}+{\frac {4}{15}}x^{5}-\cdots ,}$$ while for large ${\displaystyle x}$ it has the asymptotic expansion $${\displaystyle F(x)={\frac {1}{2x}}+{\frac {1}{4x^{3}}}+{\frac {3}{8x^{5}}}+\cdots .}$$

More precisely $${\displaystyle \left|F(x)-\sum _{k=0}^{N}{\frac {(2k-1)!!}{2^{k+1}x^{2k+1}}}\right|\leq {\frac {C_{N}}{x^{2N+3}}}.}$$ where ${\displaystyle n!!}$ is the double factorial.

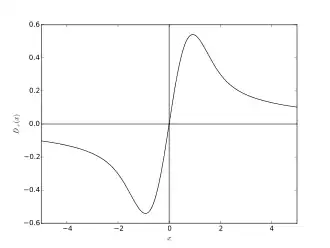
${\displaystyle F(x)}$ satisfies the differential equation $${\displaystyle {\frac {dF}{dx}}+2xF=1\,\!}$$ with the initial condition ${\displaystyle F(0)=0.}$ Consequently, it has extrema for $${\displaystyle F(x)={\frac {1}{2x}},}$$ resulting in x = ±0.92413887... (OEIS: A133841), F(x) = ±0.54104422... (OEIS: A133842).

Inflection points follow for $${\displaystyle F(x)={\frac {x}{2x^{2}-1}},}$$ resulting in x = ±1.50197526... (OEIS: A133843), F(x) = ±0.42768661... (OEIS: A245262). (Apart from the trivial inflection point at ${\displaystyle x=0,}$ ${\displaystyle F(x)=0.}$)

The Hilbert transform of the Gaussian is defined as $${\displaystyle H(y)=\pi ^{-1}\operatorname {P.V.} \int _{-\infty }^{\infty }{\frac {e^{-x^{2}}}{y-x}}\,dx}$$

P.V. denotes the Cauchy principal value, and we restrict ourselves to real ${\displaystyle y.}$ ${\displaystyle H(y)}$ can be related to the Dawson function as follows. Inside a principal value integral, we can treat ${\displaystyle 1/u}$ as a generalized function or distribution, and use the Fourier representation $${\displaystyle {1 \over u}=\int _{0}^{\infty }dk\,\sin ku=\int _{0}^{\infty }dk\,\operatorname {Im} e^{iku}.}$$

With ${\displaystyle 1/u=1/(y-x),}$ we use the exponential representation of ${\displaystyle \sin(ku)}$ and complete the square with respect to ${\displaystyle x}$ to find $${\displaystyle \pi H(y)=\operatorname {Im} \int _{0}^{\infty }dk\,\exp[-k^{2}/4+iky]\int _{-\infty }^{\infty }dx\,\exp[-(x+ik/2)^{2}].}$$

We can shift the integral over ${\displaystyle x}$ to the real axis, and it gives ${\displaystyle \pi ^{1/2}.}$ Thus $${\displaystyle \pi ^{1/2}H(y)=\operatorname {Im} \int _{0}^{\infty }dk\,\exp[-k^{2}/4+iky].}$$

We complete the square with respect to ${\displaystyle k}$ and obtain $${\displaystyle \pi ^{1/2}H(y)=e^{-y^{2}}\operatorname {Im} \int _{0}^{\infty }dk\,\exp[-(k/2-iy)^{2}].}$$

We change variables to ${\displaystyle u=ik/2+y:}$ $${\displaystyle \pi ^{1/2}H(y)=-2e^{-y^{2}}\operatorname {Im} i\int _{y}^{i\infty +y}du\ e^{u^{2}}.}$$

The integral can be performed as a contour integral around a rectangle in the complex plane. Taking the imaginary part of the result gives $${\displaystyle H(y)=2\pi ^{-1/2}F(y)}$$ where ${\displaystyle F(y)}$ is the Dawson function as defined above.

The Hilbert transform of ${\displaystyle x^{2n}e^{-x^{2}}}$ is also related to the Dawson function. We see this with the technique of differentiating inside the integral sign. Let $${\displaystyle H_{n}=\pi ^{-1}\operatorname {P.V.} \int _{-\infty }^{\infty }{\frac {x^{2n}e^{-x^{2}}}{y-x}}\,dx.}$$

Introduce $${\displaystyle H_{a}=\pi ^{-1}\operatorname {P.V.} \int _{-\infty }^{\infty }{e^{-ax^{2}} \over y-x}\,dx.}$$

The ${\displaystyle n}$th derivative is $${\displaystyle {\partial ^{n}H_{a} \over \partial a^{n}}=(-1)^{n}\pi ^{-1}\operatorname {P.V.} \int _{-\infty }^{\infty }{\frac {x^{2n}e^{-ax^{2}}}{y-x}}\,dx.}$$

We thus find $${\displaystyle \left.H_{n}=(-1)^{n}{\frac {\partial ^{n}H_{a}}{\partial a^{n}}}\right|_{a=1}.}$$

The derivatives are performed first, then the result evaluated at ${\displaystyle a=1.}$ A change of variable also gives ${\displaystyle H_{a}=2\pi ^{-1/2}F(y{\sqrt {a}}).}$ Since ${\displaystyle F'(y)=1-2yF(y),}$ we can write ${\displaystyle H_{n}=P_{1}(y)+P_{2}(y)F(y)}$ where ${\displaystyle P_{1}}$ and ${\displaystyle P_{2}}$ are polynomials. For example, ${\displaystyle H_{1}=-\pi ^{-1/2}y+2\pi ^{-1/2}y^{2}F(y).}$ Alternatively, ${\displaystyle H_{n}}$ can be calculated using the recurrence relation (for ${\displaystyle n\geq 0}$) $${\displaystyle H_{n+1}(y)=y^{2}H_{n}(y)-{\frac {(2n-1)!!}{{\sqrt {\pi }}2^{n}}}y.}$$

• List of mathematical functions

• gsl_sf_dawson in the GNU Scientific Library
• libcerf, numeric C library for complex error functions, provides a function voigt(x, sigma, gamma) with approximately 13–14 digits precision. It is based on the Faddeeva function as implemented in the MIT Faddeeva Package
• Dawson's Integral (at Mathworld)
• Error functions