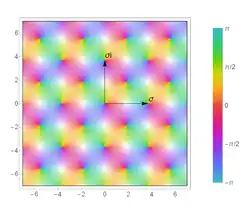
The lemniscate sine (red) and lemniscate cosine (purple) applied to a real argument, in comparison with the trigonometric sine y = sin(πx /ϖ ) In mathematics , the lemniscate elliptic functions are elliptic functions related to the arc length of the lemniscate of Bernoulli . They were first studied by Giulio Fagnano in 1718 and later by Leonhard Euler and Carl Friedrich Gauss , among others.[ 1]
The lemniscate sine and lemniscate cosine functions, usually written with the symbols sl and cl (sometimes the symbols sinlem and coslem or sin lemn and cos lemn are used instead),[ 2] trigonometric functions sine and cosine. While the trigonometric sine relates the arc length to the chord length in a unit-diameter circle
x
2
+
y
2
=
x
,
{\displaystyle x^{2}+y^{2}=x,}
[ 3]
(
x
2
+
y
2
)
2
=
x
2
−
y
2
.
{\displaystyle {\bigl (}x^{2}+y^{2}{\bigr )}{}^{2}=x^{2}-y^{2}.}
The lemniscate functions have periods related to a number
ϖ
=
{\displaystyle \varpi =}
lemniscate constant , the ratio of a lemniscate's perimeter to its diameter. This number is a quartic analog of the (quadratic )
π
=
{\displaystyle \pi =}
ratio of perimeter to diameter of a circle .
As complex functions , sl and cl have a square period lattice (a multiple of the Gaussian integers ) with fundamental periods
{
(
1
+
i
)
ϖ
,
(
1
−
i
)
ϖ
}
,
{\displaystyle \{(1+i)\varpi ,(1-i)\varpi \},}
[ 4] Jacobi elliptic functions on that lattice,
sl
z
=
sn
(
z
;
−
1
)
,
{\displaystyle \operatorname {sl} z=\operatorname {sn} (z;-1),}
cl
z
=
cd
(
z
;
−
1
)
{\displaystyle \operatorname {cl} z=\operatorname {cd} (z;-1)}
Similarly, the hyperbolic lemniscate sine slh and hyperbolic lemniscate cosine clh have a square period lattice with fundamental periods
{
2
ϖ
,
2
ϖ
i
}
.
{\displaystyle {\bigl \{}{\sqrt {2}}\varpi ,{\sqrt {2}}\varpi i{\bigr \}}.}
The lemniscate functions and the hyperbolic lemniscate functions are related to the Weierstrass elliptic function
℘
(
z
;
a
,
0
)
{\displaystyle \wp (z;a,0)}
Lemniscate sine and cosine functions
Definitions
The lemniscate functions sl and cl can be defined as the solution to the initial value problem :[ 5]
d
d
z
sl
z
=
(
1
+
sl
2
z
)
cl
z
,
d
d
z
cl
z
=
−
(
1
+
cl
2
z
)
sl
z
,
sl
0
=
0
,
cl
0
=
1
,
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {sl} z={\bigl (}1+\operatorname {sl} ^{2}z{\bigr )}\operatorname {cl} z,\ {\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {cl} z=-{\bigl (}1+\operatorname {cl} ^{2}z{\bigr )}\operatorname {sl} z,\ \operatorname {sl} 0=0,\ \operatorname {cl} 0=1,}
or equivalently as the inverses of an elliptic integral , the Schwarz–Christoffel map from the complex unit disk to a square with corners
{
1
2
ϖ
,
1
2
ϖ
i
,
−
1
2
ϖ
,
−
1
2
ϖ
i
}
:
{\displaystyle {\big \{}{\tfrac {1}{2}}\varpi ,{\tfrac {1}{2}}\varpi i,-{\tfrac {1}{2}}\varpi ,-{\tfrac {1}{2}}\varpi i{\big \}}\colon }
[ 6]
z
=
∫
0
sl
z
d
t
1
−
t
4
=
∫
cl
z
1
d
t
1
−
t
4
.
{\displaystyle z=\int _{0}^{\operatorname {sl} z}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}=\int _{\operatorname {cl} z}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}.}
Beyond that square, the functions can be extended to the complex plane via analytic continuation by successive reflections .
By comparison, the circular sine and cosine can be defined as the solution to the initial value problem:
d
d
z
sin
z
=
cos
z
,
d
d
z
cos
z
=
−
sin
z
,
sin
0
=
0
,
cos
0
=
1
,
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\sin z=\cos z,\ {\frac {\mathrm {d} }{\mathrm {d} z}}\cos z=-\sin z,\ \sin 0=0,\ \cos 0=1,}
or as inverses of a map from the upper half-plane to a half-infinite strip with real part between
−
1
2
π
,
1
2
π
{\displaystyle -{\tfrac {1}{2}}\pi ,{\tfrac {1}{2}}\pi }
z
=
∫
0
sin
z
d
t
1
−
t
2
=
∫
cos
z
1
d
t
1
−
t
2
.
{\displaystyle z=\int _{0}^{\sin z}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}=\int _{\cos z}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{2}}}}.}
Relation to the lemniscate constant
The lemniscate sine function and hyperbolic lemniscate sine functions are defined as inverses of elliptic integrals. The complete integrals are related to the lemniscate constant ϖ . The lemniscate functions have minimal real period
2
ϖ
{\displaystyle 2\varpi }
, minimal imaginary period
2
ϖ
i
{\displaystyle 2\varpi i}
and fundamental complex periods
(
1
+
i
)
ϖ
{\displaystyle (1+i)\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-i)\varpi }
ϖ
{\displaystyle \varpi }
called the lemniscate constant [ 7]
ϖ
=
2
∫
0
1
d
t
1
−
t
4
=
2.62205
…
{\displaystyle \varpi =2\int _{0}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}=2.62205\ldots }
The lemniscate functions satisfy the basic relation
cl
z
=
sl
(
1
2
ϖ
−
z
)
,
{\displaystyle \operatorname {cl} z={\operatorname {sl} }{\bigl (}{\tfrac {1}{2}}\varpi -z{\bigr )},}
cos
z
=
sin
(
1
2
π
−
z
)
.
{\displaystyle \cos z={\sin }{\bigl (}{\tfrac {1}{2}}\pi -z{\bigr )}.}
The lemniscate constant
ϖ
{\displaystyle \varpi }
is a close analog of the circle constant
π
{\displaystyle \pi }
, and many identities involving
π
{\displaystyle \pi }
have analogues involving
ϖ
{\displaystyle \varpi }
, as identities involving the trigonometric functions have analogues involving the lemniscate functions. For example, Viète's formula for
π
{\displaystyle \pi }
can be written:
2
π
=
1
2
⋅
1
2
+
1
2
1
2
⋅
1
2
+
1
2
1
2
+
1
2
1
2
⋯
{\displaystyle {\frac {2}{\pi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\sqrt {\frac {1}{2}}}}}}}\cdots }
An analogous formula for
ϖ
{\displaystyle \varpi }
is:[ 8]
2
ϖ
=
1
2
⋅
1
2
+
1
2
/
1
2
⋅
1
2
+
1
2
/
1
2
+
1
2
/
1
2
⋯
{\displaystyle {\frac {2}{\varpi }}={\sqrt {\frac {1}{2}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}\cdot {\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\Bigg /}\!{\sqrt {{\frac {1}{2}}+{\frac {1}{2}}{\bigg /}\!{\sqrt {\frac {1}{2}}}}}}}\cdots }
The Machin formula for
π
{\displaystyle \pi }
is
1
4
π
=
4
arctan
1
5
−
arctan
1
239
,
{\textstyle {\tfrac {1}{4}}\pi =4\arctan {\tfrac {1}{5}}-\arctan {\tfrac {1}{239}},}
π
{\displaystyle \pi }
can be developed using trigonometric angle sum identities, e.g. Euler's formula
1
4
π
=
arctan
1
2
+
arctan
1
3
{\textstyle {\tfrac {1}{4}}\pi =\arctan {\tfrac {1}{2}}+\arctan {\tfrac {1}{3}}}
ϖ
{\displaystyle \varpi }
, including the following found by Gauss:
1
2
ϖ
=
2
arcsl
1
2
+
arcsl
7
23
.
{\displaystyle {\tfrac {1}{2}}\varpi =2\operatorname {arcsl} {\tfrac {1}{2}}+\operatorname {arcsl} {\tfrac {7}{23}}.}
[ 9]
The lemniscate and circle constants were found by Gauss to be related to each-other by the arithmetic-geometric mean
M
{\displaystyle M}
:[ 10]
π
ϖ
=
M
(
1
,
2
)
{\displaystyle {\frac {\pi }{\varpi }}=M{\left(1,{\sqrt {2}}\!~\right)}}
Argument identities
sl
{\displaystyle \operatorname {sl} }
[ 11]
(
1
+
i
)
ϖ
{\displaystyle (1+i)\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-i)\varpi }
The lemniscate functions cl and sl are even and odd functions , respectively,
cl
(
−
z
)
=
cl
z
sl
(
−
z
)
=
−
sl
z
{\displaystyle {\begin{aligned}\operatorname {cl} (-z)&=\operatorname {cl} z\\[6mu]\operatorname {sl} (-z)&=-\operatorname {sl} z\end{aligned}}}
At translations of
1
2
ϖ
,
{\displaystyle {\tfrac {1}{2}}\varpi ,}
cl and sl are exchanged, and at translations of
1
2
i
ϖ
{\displaystyle {\tfrac {1}{2}}i\varpi }
reciprocated :[ 12]
cl
(
z
±
1
2
ϖ
)
=
∓
sl
z
,
cl
(
z
±
1
2
i
ϖ
)
=
∓
i
sl
z
sl
(
z
±
1
2
ϖ
)
=
±
cl
z
,
sl
(
z
±
1
2
i
ϖ
)
=
±
i
cl
z
{\displaystyle {\begin{aligned}{\operatorname {cl} }{\bigl (}z\pm {\tfrac {1}{2}}\varpi {\bigr )}&=\mp \operatorname {sl} z,&{\operatorname {cl} }{\bigl (}z\pm {\tfrac {1}{2}}i\varpi {\bigr )}&={\frac {\mp i}{\operatorname {sl} z}}\\[6mu]{\operatorname {sl} }{\bigl (}z\pm {\tfrac {1}{2}}\varpi {\bigr )}&=\pm \operatorname {cl} z,&{\operatorname {sl} }{\bigl (}z\pm {\tfrac {1}{2}}i\varpi {\bigr )}&={\frac {\pm i}{\operatorname {cl} z}}\end{aligned}}}
Doubling these to translations by a unit -Gaussian-integer multiple of
ϖ
{\displaystyle \varpi }
±
ϖ
{\displaystyle \pm \varpi }
±
i
ϖ
{\displaystyle \pm i\varpi }
involution :
cl
(
z
+
ϖ
)
=
cl
(
z
+
i
ϖ
)
=
−
cl
z
sl
(
z
+
ϖ
)
=
sl
(
z
+
i
ϖ
)
=
−
sl
z
{\displaystyle {\begin{aligned}\operatorname {cl} (z+\varpi )&=\operatorname {cl} (z+i\varpi )=-\operatorname {cl} z\\[4mu]\operatorname {sl} (z+\varpi )&=\operatorname {sl} (z+i\varpi )=-\operatorname {sl} z\end{aligned}}}
As a result, both functions are invariant under translation by an even-Gaussian-integer multiple of
ϖ
{\displaystyle \varpi }
[ 13]
(
a
+
b
i
)
ϖ
,
{\displaystyle (a+bi)\varpi ,}
a
+
b
=
2
k
{\displaystyle a+b=2k}
a
{\displaystyle a}
,
b
{\displaystyle b}
, and
k
{\displaystyle k}
.
cl
(
z
+
(
1
+
i
)
ϖ
)
=
cl
(
z
+
(
1
−
i
)
ϖ
)
=
cl
z
sl
(
z
+
(
1
+
i
)
ϖ
)
=
sl
(
z
+
(
1
−
i
)
ϖ
)
=
sl
z
{\displaystyle {\begin{aligned}{\operatorname {cl} }{\bigl (}z+(1+i)\varpi {\bigr )}&={\operatorname {cl} }{\bigl (}z+(1-i)\varpi {\bigr )}=\operatorname {cl} z\\[4mu]{\operatorname {sl} }{\bigl (}z+(1+i)\varpi {\bigr )}&={\operatorname {sl} }{\bigl (}z+(1-i)\varpi {\bigr )}=\operatorname {sl} z\end{aligned}}}
This makes them elliptic functions (doubly periodic meromorphic functions in the complex plane) with a diagonal square period lattice of fundamental periods
(
1
+
i
)
ϖ
{\displaystyle (1+i)\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-i)\varpi }
[ 14]
Reflections and quarter-turn rotations of lemniscate function arguments have simple expressions:
cl
z
¯
=
cl
z
¯
sl
z
¯
=
sl
z
¯
cl
i
z
=
1
cl
z
sl
i
z
=
i
sl
z
{\displaystyle {\begin{aligned}\operatorname {cl} {\bar {z}}&={\overline {\operatorname {cl} z}}\\[6mu]\operatorname {sl} {\bar {z}}&={\overline {\operatorname {sl} z}}\\[4mu]\operatorname {cl} iz&={\frac {1}{\operatorname {cl} z}}\\[6mu]\operatorname {sl} iz&=i\operatorname {sl} z\end{aligned}}}
The sl function has simple zeros at Gaussian integer multiples of
ϖ
{\displaystyle \varpi }
, complex numbers of the form
a
ϖ
+
b
ϖ
i
{\displaystyle a\varpi +b\varpi i}
a
{\displaystyle a}
and
b
{\displaystyle b}
. It has simple poles at Gaussian half-integer multiples of
ϖ
{\displaystyle \varpi }
, complex numbers of the form
(
a
+
1
2
)
ϖ
+
(
b
+
1
2
)
ϖ
i
{\displaystyle {\bigl (}a+{\tfrac {1}{2}}{\bigr )}\varpi +{\bigl (}b+{\tfrac {1}{2}}{\bigr )}\varpi i}
residues
(
−
1
)
a
−
b
+
1
i
{\displaystyle (-1)^{a-b+1}i}
cl function is reflected and offset from the sl function,
cl
z
=
sl
(
1
2
ϖ
−
z
)
{\displaystyle \operatorname {cl} z={\operatorname {sl} }{\bigl (}{\tfrac {1}{2}}\varpi -z{\bigr )}}
(
a
+
1
2
)
ϖ
+
b
ϖ
i
{\displaystyle {\bigl (}a+{\tfrac {1}{2}}{\bigr )}\varpi +b\varpi i}
a
ϖ
+
(
b
+
1
2
)
ϖ
i
,
{\displaystyle a\varpi +{\bigl (}b+{\tfrac {1}{2}}{\bigr )}\varpi i,}
(
−
1
)
a
−
b
i
.
{\displaystyle (-1)^{a-b}i.}
Also
sl
z
=
sl
w
↔
z
=
(
−
1
)
m
+
n
w
+
(
m
+
n
i
)
ϖ
{\displaystyle \operatorname {sl} z=\operatorname {sl} w\leftrightarrow z=(-1)^{m+n}w+(m+ni)\varpi }
for some
m
,
n
∈
Z
{\displaystyle m,n\in \mathbb {Z} }
sl
(
(
1
±
i
)
z
)
=
(
1
±
i
)
sl
z
sl
′
z
.
{\displaystyle \operatorname {sl} ((1\pm i)z)=(1\pm i){\frac {\operatorname {sl} z}{\operatorname {sl} 'z}}.}
The last formula is a special case of complex multiplication . Analogous formulas can be given for
sl
(
(
n
+
m
i
)
z
)
{\displaystyle \operatorname {sl} ((n+mi)z)}
n
+
m
i
{\displaystyle n+mi}
sl
{\displaystyle \operatorname {sl} }
Z
[
i
]
{\displaystyle \mathbb {Z} [i]}
[ 15]
There are also infinite series reflecting the distribution of the zeros and poles of sl :[ 16] [ 17]
1
sl
z
=
∑
(
n
,
k
)
∈
Z
2
(
−
1
)
n
+
k
z
+
n
ϖ
+
k
ϖ
i
{\displaystyle {\frac {1}{\operatorname {sl} z}}=\sum _{(n,k)\in \mathbb {Z} ^{2}}{\frac {(-1)^{n+k}}{z+n\varpi +k\varpi i}}}
sl
z
=
−
i
∑
(
n
,
k
)
∈
Z
2
(
−
1
)
n
+
k
z
+
(
n
+
1
/
2
)
ϖ
+
(
k
+
1
/
2
)
ϖ
i
.
{\displaystyle \operatorname {sl} z=-i\sum _{(n,k)\in \mathbb {Z} ^{2}}{\frac {(-1)^{n+k}}{z+(n+1/2)\varpi +(k+1/2)\varpi i}}.}
Pythagorean-like identity
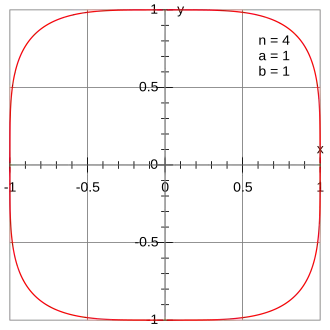
Curves x ² ⊕ y ² = a a . Negative a a a = ±1a = ∞ The lemniscate functions satisfy a Pythagorean -like identity:
c
l
2
z
+
s
l
2
z
+
c
l
2
z
s
l
2
z
=
1
{\displaystyle \operatorname {cl^{2}} z+\operatorname {sl^{2}} z+\operatorname {cl^{2}} z\,\operatorname {sl^{2}} z=1}
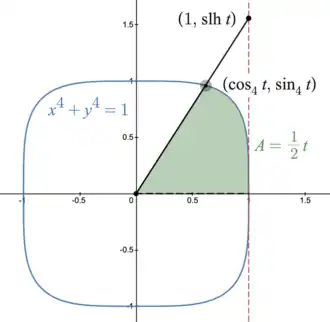
As a result, the parametric equation
(
x
,
y
)
=
(
cl
t
,
sl
t
)
{\displaystyle (x,y)=(\operatorname {cl} t,\operatorname {sl} t)}
quartic curve
x
2
+
y
2
+
x
2
y
2
=
1.
{\displaystyle x^{2}+y^{2}+x^{2}y^{2}=1.}
This identity can alternately be rewritten:[ 18]
(
1
+
c
l
2
z
)
(
1
+
s
l
2
z
)
=
2
{\displaystyle {\bigl (}1+\operatorname {cl^{2}} z{\bigr )}{\bigl (}1+\operatorname {sl^{2}} z{\bigr )}=2}
c
l
2
z
=
1
−
s
l
2
z
1
+
s
l
2
z
,
s
l
2
z
=
1
−
c
l
2
z
1
+
c
l
2
z
{\displaystyle \operatorname {cl^{2}} z={\frac {1-\operatorname {sl^{2}} z}{1+\operatorname {sl^{2}} z}},\quad \operatorname {sl^{2}} z={\frac {1-\operatorname {cl^{2}} z}{1+\operatorname {cl^{2}} z}}}
Defining a tangent-sum operator as
a
⊕
b
:=
tan
(
arctan
a
+
arctan
b
)
=
a
+
b
1
−
a
b
,
{\displaystyle a\oplus b\mathrel {:=} \tan(\arctan a+\arctan b)={\frac {a+b}{1-ab}},}
c
l
2
z
⊕
s
l
2
z
=
1.
{\displaystyle \operatorname {cl^{2}} z\oplus \operatorname {sl^{2}} z=1.}
The functions
cl
~
{\displaystyle {\tilde {\operatorname {cl} }}}
sl
~
{\displaystyle {\tilde {\operatorname {sl} }}}
(
∫
0
x
cl
~
t
d
t
)
2
+
(
1
−
∫
0
x
sl
~
t
d
t
)
2
=
1.
{\displaystyle \left(\int _{0}^{x}{\tilde {\operatorname {cl} }}\,t\,\mathrm {d} t\right)^{2}+\left(1-\int _{0}^{x}{\tilde {\operatorname {sl} }}\,t\,\mathrm {d} t\right)^{2}=1.}
Derivatives and integrals
The derivatives are as follows:
d
d
z
cl
z
=
c
l
′
z
=
−
(
1
+
c
l
2
z
)
sl
z
=
−
2
sl
z
sl
2
z
+
1
c
l
′
2
z
=
1
−
c
l
4
z
d
d
z
sl
z
=
s
l
′
z
=
(
1
+
s
l
2
z
)
cl
z
=
2
cl
z
cl
2
z
+
1
s
l
′
2
z
=
1
−
s
l
4
z
{\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {cl} z=\operatorname {cl'} z&=-{\bigl (}1+\operatorname {cl^{2}} z{\bigr )}\operatorname {sl} z=-{\frac {2\operatorname {sl} z}{\operatorname {sl} ^{2}z+1}}\\\operatorname {cl'^{2}} z&=1-\operatorname {cl^{4}} z\\[5mu]{\frac {\mathrm {d} }{\mathrm {d} z}}\operatorname {sl} z=\operatorname {sl'} z&={\bigl (}1+\operatorname {sl^{2}} z{\bigr )}\operatorname {cl} z={\frac {2\operatorname {cl} z}{\operatorname {cl} ^{2}z+1}}\\\operatorname {sl'^{2}} z&=1-\operatorname {sl^{4}} z\end{aligned}}}
d
d
z
cl
~
z
=
−
2
sl
~
z
cl
z
−
sl
~
z
cl
z
d
d
z
sl
~
z
=
2
cl
~
z
cl
z
−
cl
~
z
cl
z
{\displaystyle {\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} z}}\,{\tilde {\operatorname {cl} }}\,z&=-2\,{\tilde {\operatorname {sl} }}\,z\,\operatorname {cl} z-{\frac {{\tilde {\operatorname {sl} }}\,z}{\operatorname {cl} z}}\\{\frac {\mathrm {d} }{\mathrm {d} z}}\,{\tilde {\operatorname {sl} }}\,z&=2\,{\tilde {\operatorname {cl} }}\,z\,\operatorname {cl} z-{\frac {{\tilde {\operatorname {cl} }}\,z}{\operatorname {cl} z}}\end{aligned}}}
The second derivatives of lemniscate sine and lemniscate cosine are their negative duplicated cubes:
d
2
d
z
2
cl
z
=
−
2
c
l
3
z
{\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} z^{2}}}\operatorname {cl} z=-2\operatorname {cl^{3}} z}
d
2
d
z
2
sl
z
=
−
2
s
l
3
z
{\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} z^{2}}}\operatorname {sl} z=-2\operatorname {sl^{3}} z}
The lemniscate functions can be integrated using the inverse tangent function:
∫
cl
z
d
z
=
arctan
sl
z
+
C
∫
sl
z
d
z
=
−
arctan
cl
z
+
C
∫
cl
~
z
d
z
=
sl
~
z
cl
z
+
C
∫
sl
~
z
d
z
=
−
cl
~
z
cl
z
+
C
{\displaystyle {\begin{aligned}\int \operatorname {cl} z\mathop {\mathrm {d} z} &=\arctan \operatorname {sl} z+C\\\int \operatorname {sl} z\mathop {\mathrm {d} z} &=-\arctan \operatorname {cl} z+C\\\int {\tilde {\operatorname {cl} }}\,z\,\mathrm {d} z&={\frac {{\tilde {\operatorname {sl} }}\,z}{\operatorname {cl} z}}+C\\\int {\tilde {\operatorname {sl} }}\,z\,\mathrm {d} z&=-{\frac {{\tilde {\operatorname {cl} }}\,z}{\operatorname {cl} z}}+C\end{aligned}}}
Argument sum and multiple identities
Like the trigonometric functions, the lemniscate functions satisfy argument sum and difference identities. The original identity used by Fagnano for bisection of the lemniscate was:[ 19]
sl
(
u
+
v
)
=
sl
u
s
l
′
v
+
sl
v
s
l
′
u
1
+
s
l
2
u
s
l
2
v
{\displaystyle \operatorname {sl} (u+v)={\frac {\operatorname {sl} u\,\operatorname {sl'} v+\operatorname {sl} v\,\operatorname {sl'} u}{1+\operatorname {sl^{2}} u\,\operatorname {sl^{2}} v}}}
The derivative and Pythagorean-like identities can be used to rework the identity used by Fagano in terms of sl and cl . Defining a tangent-sum operator
a
⊕
b
:=
tan
(
arctan
a
+
arctan
b
)
{\displaystyle a\oplus b\mathrel {:=} \tan(\arctan a+\arctan b)}
a
⊖
b
:=
a
⊕
(
−
b
)
,
{\displaystyle a\ominus b\mathrel {:=} a\oplus (-b),}
[ 20]
cl
(
u
+
v
)
=
cl
u
cl
v
⊖
sl
u
sl
v
=
cl
u
cl
v
−
sl
u
sl
v
1
+
sl
u
cl
u
sl
v
cl
v
cl
(
u
−
v
)
=
cl
u
cl
v
⊕
sl
u
sl
v
sl
(
u
+
v
)
=
sl
u
cl
v
⊕
cl
u
sl
v
=
sl
u
cl
v
+
cl
u
sl
v
1
−
sl
u
cl
u
sl
v
cl
v
sl
(
u
−
v
)
=
sl
u
cl
v
⊖
cl
u
sl
v
{\displaystyle {\begin{aligned}\operatorname {cl} (u+v)&=\operatorname {cl} u\,\operatorname {cl} v\ominus \operatorname {sl} u\,\operatorname {sl} v={\frac {\operatorname {cl} u\,\operatorname {cl} v-\operatorname {sl} u\,\operatorname {sl} v}{1+\operatorname {sl} u\,\operatorname {cl} u\,\operatorname {sl} v\,\operatorname {cl} v}}\\[2mu]\operatorname {cl} (u-v)&=\operatorname {cl} u\,\operatorname {cl} v\oplus \operatorname {sl} u\,\operatorname {sl} v\\[2mu]\operatorname {sl} (u+v)&=\operatorname {sl} u\,\operatorname {cl} v\oplus \operatorname {cl} u\,\operatorname {sl} v={\frac {\operatorname {sl} u\,\operatorname {cl} v+\operatorname {cl} u\,\operatorname {sl} v}{1-\operatorname {sl} u\,\operatorname {cl} u\,\operatorname {sl} v\,\operatorname {cl} v}}\\[2mu]\operatorname {sl} (u-v)&=\operatorname {sl} u\,\operatorname {cl} v\ominus \operatorname {cl} u\,\operatorname {sl} v\end{aligned}}}
These resemble their trigonometric analogs :
cos
(
u
±
v
)
=
cos
u
cos
v
∓
sin
u
sin
v
sin
(
u
±
v
)
=
sin
u
cos
v
±
cos
u
sin
v
{\displaystyle {\begin{aligned}\cos(u\pm v)&=\cos u\,\cos v\mp \sin u\,\sin v\\[6mu]\sin(u\pm v)&=\sin u\,\cos v\pm \cos u\,\sin v\end{aligned}}}
In particular, to compute the complex-valued functions in real components,
cl
(
x
+
i
y
)
=
cl
x
−
i
sl
x
sl
y
cl
y
cl
y
+
i
sl
x
cl
x
sl
y
=
cl
x
cl
y
(
1
−
sl
2
x
sl
2
y
)
cl
2
y
+
sl
2
x
cl
2
x
sl
2
y
−
i
sl
x
sl
y
(
cl
2
x
+
cl
2
y
)
cl
2
y
+
sl
2
x
cl
2
x
sl
2
y
sl
(
x
+
i
y
)
=
sl
x
+
i
cl
x
sl
y
cl
y
cl
y
−
i
sl
x
cl
x
sl
y
=
sl
x
cl
y
(
1
−
cl
2
x
sl
2
y
)
cl
2
y
+
sl
2
x
cl
2
x
sl
2
y
+
i
cl
x
sl
y
(
sl
2
x
+
cl
2
y
)
cl
2
y
+
sl
2
x
cl
2
x
sl
2
y
{\displaystyle {\begin{aligned}\operatorname {cl} (x+iy)&={\frac {\operatorname {cl} x-i\operatorname {sl} x\,\operatorname {sl} y\,\operatorname {cl} y}{\operatorname {cl} y+i\operatorname {sl} x\,\operatorname {cl} x\,\operatorname {sl} y}}\\[4mu]&={\frac {\operatorname {cl} x\,\operatorname {cl} y\left(1-\operatorname {sl} ^{2}x\,\operatorname {sl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}-i{\frac {\operatorname {sl} x\,\operatorname {sl} y\left(\operatorname {cl} ^{2}x+\operatorname {cl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}\\[12mu]\operatorname {sl} (x+iy)&={\frac {\operatorname {sl} x+i\operatorname {cl} x\,\operatorname {sl} y\,\operatorname {cl} y}{\operatorname {cl} y-i\operatorname {sl} x\,\operatorname {cl} x\,\operatorname {sl} y}}\\[4mu]&={\frac {\operatorname {sl} x\,\operatorname {cl} y\left(1-\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}+i{\frac {\operatorname {cl} x\,\operatorname {sl} y\left(\operatorname {sl} ^{2}x+\operatorname {cl} ^{2}y\right)}{\operatorname {cl} ^{2}y+\operatorname {sl} ^{2}x\,\operatorname {cl} ^{2}x\,\operatorname {sl} ^{2}y}}\end{aligned}}}
Gauss discovered that
sl
(
u
−
v
)
sl
(
u
+
v
)
=
sl
(
(
1
+
i
)
u
)
−
sl
(
(
1
+
i
)
v
)
sl
(
(
1
+
i
)
u
)
+
sl
(
(
1
+
i
)
v
)
{\displaystyle {\frac {\operatorname {sl} (u-v)}{\operatorname {sl} (u+v)}}={\frac {\operatorname {sl} ((1+i)u)-\operatorname {sl} ((1+i)v)}{\operatorname {sl} ((1+i)u)+\operatorname {sl} ((1+i)v)}}}
where
u
,
v
∈
C
{\displaystyle u,v\in \mathbb {C} }
Also
sl
(
u
+
v
)
sl
(
u
−
v
)
=
sl
2
u
−
sl
2
v
1
+
sl
2
u
sl
2
v
{\displaystyle \operatorname {sl} (u+v)\operatorname {sl} (u-v)={\frac {\operatorname {sl} ^{2}u-\operatorname {sl} ^{2}v}{1+\operatorname {sl} ^{2}u\operatorname {sl} ^{2}v}}}
where
u
,
v
∈
C
{\displaystyle u,v\in \mathbb {C} }
sin
(
u
+
v
)
sin
(
u
−
v
)
=
sin
2
u
−
sin
2
v
.
{\displaystyle \sin(u+v)\sin(u-v)=\sin ^{2}u-\sin ^{2}v.}
Bisection formulas:
cl
2
1
2
x
=
1
+
cl
x
1
+
sl
2
x
1
+
1
+
sl
2
x
{\displaystyle \operatorname {cl} ^{2}{\tfrac {1}{2}}x={\frac {1+\operatorname {cl} x{\sqrt {1+\operatorname {sl} ^{2}x}}}{1+{\sqrt {1+\operatorname {sl} ^{2}x}}}}}
sl
2
1
2
x
=
1
−
cl
x
1
+
sl
2
x
1
+
1
+
sl
2
x
{\displaystyle \operatorname {sl} ^{2}{\tfrac {1}{2}}x={\frac {1-\operatorname {cl} x{\sqrt {1+\operatorname {sl} ^{2}x}}}{1+{\sqrt {1+\operatorname {sl} ^{2}x}}}}}
Duplication formulas:[ 21]
cl
2
x
=
−
1
+
2
cl
2
x
+
cl
4
x
1
+
2
cl
2
x
−
cl
4
x
{\displaystyle \operatorname {cl} 2x={\frac {-1+2\,\operatorname {cl} ^{2}x+\operatorname {cl} ^{4}x}{1+2\,\operatorname {cl} ^{2}x-\operatorname {cl} ^{4}x}}}
sl
2
x
=
2
sl
x
cl
x
1
+
sl
2
x
1
+
sl
4
x
{\displaystyle \operatorname {sl} 2x=2\,\operatorname {sl} x\,\operatorname {cl} x{\frac {1+\operatorname {sl} ^{2}x}{1+\operatorname {sl} ^{4}x}}}
Triplication formulas:[ 21]
cl
3
x
=
−
3
cl
x
+
6
cl
5
x
+
cl
9
x
1
+
6
cl
4
x
−
3
cl
8
x
{\displaystyle \operatorname {cl} 3x={\frac {-3\,\operatorname {cl} x+6\,\operatorname {cl} ^{5}x+\operatorname {cl} ^{9}x}{1+6\,\operatorname {cl} ^{4}x-3\,\operatorname {cl} ^{8}x}}}
sl
3
x
=
3
sl
x
−
6
sl
5
x
−
1
sl
9
x
1
+
6
sl
4
x
−
3
sl
8
x
{\displaystyle \operatorname {sl} 3x={\frac {\color {red}{3}\,\color {black}{\operatorname {sl} x-\,}\color {green}{6}\,\color {black}{\operatorname {sl} ^{5}x-\,}\color {blue}{1}\,\color {black}{\operatorname {sl} ^{9}x}}{\color {blue}{1}\,\color {black}{+\,}\,\color {green}{6}\,\color {black}{\operatorname {sl} ^{4}x-\,}\color {red}{3}\,\color {black}{\operatorname {sl} ^{8}x}}}}
Note the "reverse symmetry" of the coefficients of numerator and denominator of
sl
3
x
{\displaystyle \operatorname {sl} 3x}
sl
β
x
{\displaystyle \operatorname {sl} \beta x}
β
=
m
+
n
i
{\displaystyle \beta =m+ni}
m
,
n
∈
Z
{\displaystyle m,n\in \mathbb {Z} }
m
+
n
{\displaystyle m+n}
[ 15]
Lemnatomic polynomials
Let
L
{\displaystyle L}
lattice
L
=
Z
(
1
+
i
)
ϖ
+
Z
(
1
−
i
)
ϖ
.
{\displaystyle L=\mathbb {Z} (1+i)\varpi +\mathbb {Z} (1-i)\varpi .}
Furthermore, let
K
=
Q
(
i
)
{\displaystyle K=\mathbb {Q} (i)}
O
=
Z
[
i
]
{\displaystyle {\mathcal {O}}=\mathbb {Z} [i]}
z
∈
C
{\displaystyle z\in \mathbb {C} }
β
=
m
+
i
n
{\displaystyle \beta =m+in}
γ
=
m
′
+
i
n
′
{\displaystyle \gamma =m'+in'}
m
,
n
,
m
′
,
n
′
∈
Z
{\displaystyle m,n,m',n'\in \mathbb {Z} }
m
+
n
{\displaystyle m+n}
m
′
+
n
′
{\displaystyle m'+n'}
γ
≡
1
mod
2
(
1
+
i
)
{\displaystyle \gamma \equiv 1\,\operatorname {mod} \,2(1+i)}
sl
β
z
=
M
β
(
sl
z
)
{\displaystyle \operatorname {sl} \beta z=M_{\beta }(\operatorname {sl} z)}
M
β
(
x
)
=
i
ε
x
P
β
(
x
4
)
Q
β
(
x
4
)
{\displaystyle M_{\beta }(x)=i^{\varepsilon }x{\frac {P_{\beta }(x^{4})}{Q_{\beta }(x^{4})}}}
for some coprime polynomials
P
β
(
x
)
,
Q
β
(
x
)
∈
O
[
x
]
{\displaystyle P_{\beta }(x),Q_{\beta }(x)\in {\mathcal {O}}[x]}
ε
∈
{
0
,
1
,
2
,
3
}
{\displaystyle \varepsilon \in \{0,1,2,3\}}
[ 22]
x
P
β
(
x
4
)
=
∏
γ
|
β
Λ
γ
(
x
)
{\displaystyle xP_{\beta }(x^{4})=\prod _{\gamma |\beta }\Lambda _{\gamma }(x)}
and
Λ
β
(
x
)
=
∏
[
α
]
∈
(
O
/
β
O
)
×
(
x
−
sl
α
δ
β
)
{\displaystyle \Lambda _{\beta }(x)=\prod _{[\alpha ]\in ({\mathcal {O}}/\beta {\mathcal {O}})^{\times }}(x-\operatorname {sl} \alpha \delta _{\beta })}
where
δ
β
{\displaystyle \delta _{\beta }}
β
{\displaystyle \beta }
torsion generator (i.e.
δ
β
∈
(
1
/
β
)
L
{\displaystyle \delta _{\beta }\in (1/\beta )L}
[
δ
β
]
∈
(
1
/
β
)
L
/
L
{\displaystyle [\delta _{\beta }]\in (1/\beta )L/L}
(
1
/
β
)
L
/
L
{\displaystyle (1/\beta )L/L}
O
{\displaystyle {\mathcal {O}}}
module ). Examples of
β
{\displaystyle \beta }
2
ϖ
/
β
{\displaystyle 2\varpi /\beta }
(
1
+
i
)
ϖ
/
β
{\displaystyle (1+i)\varpi /\beta }
Λ
β
(
x
)
∈
O
[
x
]
{\displaystyle \Lambda _{\beta }(x)\in {\mathcal {O}}[x]}
β
{\displaystyle \beta }
lemnatomic polynomial . It is monic and is irreducible over
K
{\displaystyle K}
cyclotomic polynomials ,[ 23]
Φ
k
(
x
)
=
∏
[
a
]
∈
(
Z
/
k
Z
)
×
(
x
−
ζ
k
a
)
.
{\displaystyle \Phi _{k}(x)=\prod _{[a]\in (\mathbb {Z} /k\mathbb {Z} )^{\times }}(x-\zeta _{k}^{a}).}
The
β
{\displaystyle \beta }
Λ
β
(
x
)
{\displaystyle \Lambda _{\beta }(x)}
minimal polynomial of
sl
δ
β
{\displaystyle \operatorname {sl} \delta _{\beta }}
K
[
x
]
{\displaystyle K[x]}
ω
β
=
sl
(
2
ϖ
/
β
)
{\displaystyle \omega _{\beta }=\operatorname {sl} (2\varpi /\beta )}
ω
~
β
=
sl
(
(
1
+
i
)
ϖ
/
β
)
{\displaystyle {\tilde {\omega }}_{\beta }=\operatorname {sl} ((1+i)\varpi /\beta )}
ω
5
{\displaystyle \omega _{5}}
ω
~
5
{\displaystyle {\tilde {\omega }}_{5}}
K
[
x
]
{\displaystyle K[x]}
Λ
5
(
x
)
=
x
16
+
52
x
12
−
26
x
8
−
12
x
4
+
1
,
{\displaystyle \Lambda _{5}(x)=x^{16}+52x^{12}-26x^{8}-12x^{4}+1,}
and[ 24]
ω
5
=
−
13
+
6
5
+
2
85
−
38
5
4
{\displaystyle \omega _{5}={\sqrt[{4}]{-13+6{\sqrt {5}}+2{\sqrt {85-38{\sqrt {5}}}}}}}
ω
~
5
=
−
13
−
6
5
+
2
85
+
38
5
4
{\displaystyle {\tilde {\omega }}_{5}={\sqrt[{4}]{-13-6{\sqrt {5}}+2{\sqrt {85+38{\sqrt {5}}}}}}}
[ 25] (an equivalent expression is given in the table below). Another example is[ 23]
Λ
−
1
+
2
i
(
x
)
=
x
4
−
1
+
2
i
{\displaystyle \Lambda _{-1+2i}(x)=x^{4}-1+2i}
which is the minimal polynomial of
ω
−
1
+
2
i
{\displaystyle \omega _{-1+2i}}
ω
~
−
1
+
2
i
{\displaystyle {\tilde {\omega }}_{-1+2i}}
K
[
x
]
.
{\displaystyle K[x].}
If
p
{\displaystyle p}
β
{\displaystyle \beta }
[ 26] [ 27]
deg
Λ
β
=
β
2
∏
p
|
β
(
1
−
1
p
)
(
1
−
(
−
1
)
(
p
−
1
)
/
2
p
)
{\displaystyle \operatorname {deg} \Lambda _{\beta }=\beta ^{2}\prod _{p|\beta }\left(1-{\frac {1}{p}}\right)\left(1-{\frac {(-1)^{(p-1)/2}}{p}}\right)}
which can be compared to the cyclotomic analog
deg
Φ
k
=
k
∏
p
|
k
(
1
−
1
p
)
.
{\displaystyle \operatorname {deg} \Phi _{k}=k\prod _{p|k}\left(1-{\frac {1}{p}}\right).}
Specific values
Just as for the trigonometric functions, values of the lemniscate functions can be computed for divisions of the lemniscate into
n
{\displaystyle n}
parts of equal length, using only basic arithmetic and square roots, if and only if
n
{\displaystyle n}
is of the form
n
=
2
k
p
1
p
2
⋯
p
m
{\displaystyle n=2^{k}p_{1}p_{2}\cdots p_{m}}
k
{\displaystyle k}
is a non-negative integer and each
p
i
{\displaystyle p_{i}}
(if any) is a distinct Fermat prime .[ 28]
n
{\displaystyle n}
cl
n
ϖ
{\displaystyle \operatorname {cl} n\varpi }
sl
n
ϖ
{\displaystyle \operatorname {sl} n\varpi }
1
{\displaystyle 1}
−
1
{\displaystyle -1}
0
{\displaystyle 0}
5
6
{\displaystyle {\tfrac {5}{6}}}
−
2
3
−
3
4
{\displaystyle -{\sqrt[{4}]{2{\sqrt {3}}-3}}}
1
2
(
3
+
1
−
12
4
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}
3
4
{\displaystyle {\tfrac {3}{4}}}
−
2
−
1
{\displaystyle -{\sqrt {{\sqrt {2}}-1}}}
2
−
1
{\displaystyle {\sqrt {{\sqrt {2}}-1}}}
2
3
{\displaystyle {\tfrac {2}{3}}}
−
1
2
(
3
+
1
−
12
4
)
{\displaystyle -{\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}
2
3
−
3
4
{\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}}}
1
2
{\displaystyle {\tfrac {1}{2}}}
0
{\displaystyle 0}
1
{\displaystyle 1}
1
3
{\displaystyle {\tfrac {1}{3}}}
1
2
(
3
+
1
−
12
4
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}
2
3
−
3
4
{\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}}}
1
4
{\displaystyle {\tfrac {1}{4}}}
2
−
1
{\displaystyle {\sqrt {{\sqrt {2}}-1}}}
2
−
1
{\displaystyle {\sqrt {{\sqrt {2}}-1}}}
1
6
{\displaystyle {\tfrac {1}{6}}}
2
3
−
3
4
{\displaystyle {\sqrt[{4}]{2{\sqrt {3}}-3}}}
1
2
(
3
+
1
−
12
4
)
{\displaystyle {\tfrac {1}{2}}{\bigl (}{\sqrt {3}}+1-{\sqrt[{4}]{12}}{\bigr )}}
Relation to geometric shapes
The lemniscate sine and cosine relate the arc length of an arc of the lemniscate to the distance of one endpoint from the origin. The trigonometric sine and cosine analogously relate the arc length of an arc of a unit-diameter circle to the distance of one endpoint from the origin.
L
{\displaystyle {\mathcal {L}}}
lemniscate of Bernoulli with unit distance from its center to its furthest point (i.e. with unit "half-width"), is essential in the theory of the lemniscate elliptic functions. It can be characterized in at least three ways:
Angular characterization: Given two points
A
{\displaystyle A}
B
{\displaystyle B}
B
′
{\displaystyle B'}
reflection of
B
{\displaystyle B}
A
{\displaystyle A}
L
{\displaystyle {\mathcal {L}}}
closure of the locus of the points
P
{\displaystyle P}
|
A
P
B
−
A
P
B
′
|
{\displaystyle |APB-APB'|}
right angle .[ 29]
Focal characterization:
L
{\displaystyle {\mathcal {L}}}
F
1
=
(
−
1
2
,
0
)
{\displaystyle F_{1}={\bigl (}{-{\tfrac {1}{\sqrt {2}}}},0{\bigr )}}
F
2
=
(
1
2
,
0
)
{\displaystyle F_{2}={\bigl (}{\tfrac {1}{\sqrt {2}}},0{\bigr )}}
1
2
{\displaystyle {\tfrac {1}{2}}}
Explicit coordinate characterization:
L
{\displaystyle {\mathcal {L}}}
quartic curve satisfying the polar equation
r
2
=
cos
2
θ
{\displaystyle r^{2}=\cos 2\theta }
Cartesian equation
(
x
2
+
y
2
)
2
=
x
2
−
y
2
.
{\displaystyle {\bigl (}x^{2}+y^{2}{\bigr )}{}^{2}=x^{2}-y^{2}.}
The perimeter of
L
{\displaystyle {\mathcal {L}}}
2
ϖ
{\displaystyle 2\varpi }
[ 30]
The points on
L
{\displaystyle {\mathcal {L}}}
r
{\displaystyle r}
x
2
+
y
2
=
r
2
{\displaystyle x^{2}+y^{2}=r^{2}}
hyperbola
x
2
−
y
2
=
r
4
{\displaystyle x^{2}-y^{2}=r^{4}}
(
x
(
r
)
,
y
(
r
)
)
=
(
1
2
r
2
(
1
+
r
2
)
,
1
2
r
2
(
1
−
r
2
)
)
.
{\displaystyle {\big (}x(r),y(r){\big )}={\biggl (}\!{\sqrt {{\tfrac {1}{2}}r^{2}{\bigl (}1+r^{2}{\bigr )}}},\,{\sqrt {{\tfrac {1}{2}}r^{2}{\bigl (}1-r^{2}{\bigr )}}}\,{\biggr )}.}
Using this parametrization with
r
∈
[
0
,
1
]
{\displaystyle r\in [0,1]}
L
{\displaystyle {\mathcal {L}}}
arc length from the origin to a point
(
x
(
r
)
,
y
(
r
)
)
{\displaystyle {\big (}x(r),y(r){\big )}}
[ 31]
∫
0
r
x
′
(
t
)
2
+
y
′
(
t
)
2
d
t
=
∫
0
r
(
1
+
2
t
2
)
2
2
(
1
+
t
2
)
+
(
1
−
2
t
2
)
2
2
(
1
−
t
2
)
d
t
=
∫
0
r
d
t
1
−
t
4
=
arcsl
r
.
{\displaystyle {\begin{aligned}&\int _{0}^{r}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\mathop {\mathrm {d} t} \\&\quad {}=\int _{0}^{r}{\sqrt {{\frac {(1+2t^{2})^{2}}{2(1+t^{2})}}+{\frac {(1-2t^{2})^{2}}{2(1-t^{2})}}}}\mathop {\mathrm {d} t} \\[6mu]&\quad {}=\int _{0}^{r}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}\\[6mu]&\quad {}=\operatorname {arcsl} r.\end{aligned}}}
Likewise, the arc length from
(
1
,
0
)
{\displaystyle (1,0)}
(
x
(
r
)
,
y
(
r
)
)
{\displaystyle {\big (}x(r),y(r){\big )}}
∫
r
1
x
′
(
t
)
2
+
y
′
(
t
)
2
d
t
=
∫
r
1
d
t
1
−
t
4
=
arccl
r
=
1
2
ϖ
−
arcsl
r
.
{\displaystyle {\begin{aligned}&\int _{r}^{1}{\sqrt {x'(t)^{2}+y'(t)^{2}}}\mathop {\mathrm {d} t} \\&\quad {}=\int _{r}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}\\[6mu]&\quad {}=\operatorname {arccl} r={\tfrac {1}{2}}\varpi -\operatorname {arcsl} r.\end{aligned}}}
Or in the inverse direction, the lemniscate sine and cosine functions give the distance from the origin as functions of arc length from the origin and the point
(
1
,
0
)
{\displaystyle (1,0)}
Analogously, the circular sine and cosine functions relate the chord length to the arc length for the unit diameter circle with polar equation
r
=
cos
θ
{\displaystyle r=\cos \theta }
x
2
+
y
2
=
x
,
{\displaystyle x^{2}+y^{2}=x,}
(
x
(
r
)
,
y
(
r
)
)
=
(
r
2
,
r
2
(
1
−
r
2
)
)
.
{\displaystyle {\big (}x(r),y(r){\big )}={\biggl (}r^{2},\,{\sqrt {r^{2}{\bigl (}1-r^{2}{\bigr )}}}\,{\biggr )}.}
Alternatively, just as the unit circle
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1}
s
{\displaystyle s}
(
1
,
0
)
{\displaystyle (1,0)}
(
x
(
s
)
,
y
(
s
)
)
=
(
cos
s
,
sin
s
)
,
{\displaystyle (x(s),y(s))=(\cos s,\sin s),}
L
{\displaystyle {\mathcal {L}}}
s
{\displaystyle s}
(
1
,
0
)
{\displaystyle (1,0)}
[ 32]
(
x
(
s
)
,
y
(
s
)
)
=
(
cl
s
1
+
sl
2
s
,
sl
s
cl
s
1
+
sl
2
s
)
=
(
cl
~
s
,
sl
~
s
)
.
{\displaystyle (x(s),y(s))=\left({\frac {\operatorname {cl} s}{\sqrt {1+\operatorname {sl} ^{2}s}}},{\frac {\operatorname {sl} s\operatorname {cl} s}{\sqrt {1+\operatorname {sl} ^{2}s}}}\right)=\left({\tilde {\operatorname {cl} }}\,s,{\tilde {\operatorname {sl} }}\,s\right).}
The notation
cl
~
,
sl
~
{\displaystyle {\tilde {\operatorname {cl} }},\,{\tilde {\operatorname {sl} }}}
The lemniscate integral and lemniscate functions satisfy an argument duplication identity discovered by Fagnano in 1718:[ 33]
∫
0
z
d
t
1
−
t
4
=
2
∫
0
u
d
t
1
−
t
4
,
if
z
=
2
u
1
−
u
4
1
+
u
4
and
0
≤
u
≤
2
−
1
.
{\displaystyle \int _{0}^{z}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}=2\int _{0}^{u}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}},\quad {\text{if }}z={\frac {2u{\sqrt {1-u^{4}}}}{1+u^{4}}}{\text{ and }}0\leq u\leq {\sqrt {{\sqrt {2}}-1}}.}
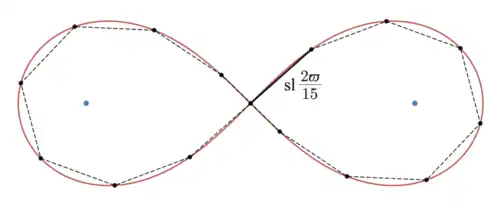
A lemniscate divided into 15 sections of equal arclength (red curves). Because the prime factors of 15 (3 and 5) are both Fermat primes, this polygon (in black) is constructible using a straightedge and compass. Later mathematicians generalized this result. Analogously to the constructible polygons in the circle, the lemniscate can be divided into
n
{\displaystyle n}
sections of equal arc length using only straightedge and compass if and only if
n
{\displaystyle n}
is of the form
n
=
2
k
p
1
p
2
⋯
p
m
{\displaystyle n=2^{k}p_{1}p_{2}\cdots p_{m}}
k
{\displaystyle k}
is a non-negative integer and each
p
i
{\displaystyle p_{i}}
(if any) is a distinct Fermat prime .[ 34] Niels Abel in 1827–1828, and the "only if" part was proved by Michael Rosen in 1981.[ 35]
n
{\displaystyle n}
sections of equal arc length using only straightedge and compass if and only if
φ
(
n
)
{\displaystyle \varphi (n)}
power of two (where
φ
{\displaystyle \varphi }
Euler's totient function ). The lemniscate is not assumed to be already drawn, as that would go against the rules of straightedge and compass constructions; instead, it is assumed that we are given only two points by which the lemniscate is defined, such as its center and radial point (one of the two points on the lemniscate such that their distance from the center is maximal) or its two foci.
Let
r
j
=
sl
2
j
ϖ
n
{\displaystyle r_{j}=\operatorname {sl} {\dfrac {2j\varpi }{n}}}
n
{\displaystyle n}
-division points for
L
{\displaystyle {\mathcal {L}}}
(
r
j
1
2
(
1
+
r
j
2
)
,
(
−
1
)
⌊
4
j
/
n
⌋
1
2
r
j
2
(
1
−
r
j
2
)
)
,
j
∈
{
1
,
2
,
…
,
n
}
{\displaystyle \left(r_{j}{\sqrt {{\tfrac {1}{2}}{\bigl (}1+r_{j}^{2}{\bigr )}}},\ (-1)^{\left\lfloor 4j/n\right\rfloor }{\sqrt {{\tfrac {1}{2}}r_{j}^{2}{\bigl (}1-r_{j}^{2}{\bigr )}}}\right),\quad j\in \{1,2,\ldots ,n\}}
where
⌊
⋅
⌋
{\displaystyle \lfloor \cdot \rfloor }
floor function . See below for some specific values of
sl
2
ϖ
n
{\displaystyle \operatorname {sl} {\dfrac {2\varpi }{n}}}
Arc length of rectangular elastica
The lemniscate sine relates the arc length to the x coordinate in the rectangular elastica. The inverse lemniscate sine also describes the arc length
s
{\displaystyle s}
relative to the
x
{\displaystyle x}
coordinate of the rectangular elastica .[ 36]
y
{\displaystyle y}
coordinate and arc length:
y
=
∫
x
1
t
2
d
t
1
−
t
4
,
s
=
arcsl
x
=
∫
0
x
d
t
1
−
t
4
{\displaystyle y=\int _{x}^{1}{\frac {t^{2}\mathop {\mathrm {d} t} }{\sqrt {1-t^{4}}}},\quad s=\operatorname {arcsl} x=\int _{0}^{x}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}}
The rectangular elastica solves a problem posed by Jacob Bernoulli , in 1691, to describe the shape of an idealized flexible rod fixed in a vertical orientation at the bottom end, and pulled down by a weight from the far end until it has been bent horizontal. Bernoulli's proposed solution established Euler–Bernoulli beam theory , further developed by Euler in the 18th century.
Elliptic characterization
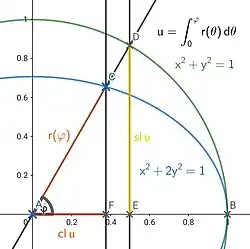
The lemniscate elliptic functions and an ellipse Let
C
{\displaystyle C}
x
2
+
2
y
2
=
1
{\displaystyle x^{2}+2y^{2}=1}
D
{\displaystyle D}
C
{\displaystyle C}
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1}
r
{\displaystyle r}
A
{\displaystyle A}
C
{\displaystyle C}
φ
{\displaystyle \varphi }
B
A
C
{\displaystyle BAC}
B
=
(
1
,
0
)
{\displaystyle B=(1,0)}
B
D
{\displaystyle BD}
u
{\displaystyle u}
u
=
∫
0
φ
r
(
θ
)
d
θ
=
∫
0
φ
d
θ
1
+
sin
2
θ
.
{\displaystyle u=\int _{0}^{\varphi }r(\theta )\,\mathrm {d} \theta =\int _{0}^{\varphi }{\frac {\mathrm {d} \theta }{\sqrt {1+\sin ^{2}\theta }}}.}
If
E
{\displaystyle E}
D
{\displaystyle D}
F
{\displaystyle F}
C
{\displaystyle C}
cl
u
=
A
F
¯
,
sl
u
=
D
E
¯
,
{\displaystyle \operatorname {cl} u={\overline {AF}},\quad \operatorname {sl} u={\overline {DE}},}
cl
~
u
=
A
F
¯
A
C
¯
,
sl
~
u
=
A
F
¯
F
C
¯
.
{\displaystyle {\tilde {\operatorname {cl} }}\,u={\overline {AF}}{\overline {AC}},\quad {\tilde {\operatorname {sl} }}\,u={\overline {AF}}{\overline {FC}}.}
Series Identities
Power series
The power series expansion of the lemniscate sine at the origin is[ 37]
sl
z
=
∑
n
=
0
∞
a
n
z
n
=
z
−
12
z
5
5
!
+
3024
z
9
9
!
−
4390848
z
13
13
!
+
⋯
,
|
z
|
<
ϖ
2
{\displaystyle \operatorname {sl} z=\sum _{n=0}^{\infty }a_{n}z^{n}=z-12{\frac {z^{5}}{5!}}+3024{\frac {z^{9}}{9!}}-4390848{\frac {z^{13}}{13!}}+\cdots ,\quad |z|<{\tfrac {\varpi }{\sqrt {2}}}}
where the coefficients
a
n
{\displaystyle a_{n}}
n
≢
1
(
mod
4
)
⟹
a
n
=
0
,
{\displaystyle n\not \equiv 1{\pmod {4}}\implies a_{n}=0,}
a
1
=
1
,
∀
n
∈
N
0
:
a
n
+
2
=
−
2
(
n
+
1
)
(
n
+
2
)
∑
i
+
j
+
k
=
n
a
i
a
j
a
k
{\displaystyle a_{1}=1,\,\forall n\in \mathbb {N} _{0}:\,a_{n+2}=-{\frac {2}{(n+1)(n+2)}}\sum _{i+j+k=n}a_{i}a_{j}a_{k}}
where
i
+
j
+
k
=
n
{\displaystyle i+j+k=n}
compositions of
n
{\displaystyle n}
a
13
{\displaystyle a_{13}}
13
−
2
=
11
{\displaystyle 13-2=11}
11
=
9
+
1
+
1
=
1
+
9
+
1
=
1
+
1
+
9
{\displaystyle 11=9+1+1=1+9+1=1+1+9}
11
=
5
+
5
+
1
=
5
+
1
+
5
=
1
+
5
+
5
{\displaystyle 11=5+5+1=5+1+5=1+5+5}
a
13
=
−
2
12
⋅
13
(
a
9
a
1
a
1
+
a
1
a
9
a
1
+
a
1
a
1
a
9
+
a
5
a
5
a
1
+
a
5
a
1
a
5
+
a
1
a
5
a
5
)
=
−
11
15600
.
{\displaystyle a_{13}=-{\tfrac {2}{12\cdot 13}}(a_{9}a_{1}a_{1}+a_{1}a_{9}a_{1}+a_{1}a_{1}a_{9}+a_{5}a_{5}a_{1}+a_{5}a_{1}a_{5}+a_{1}a_{5}a_{5})=-{\tfrac {11}{15600}}.}
The expansion can be equivalently written as[ 38]
sl
z
=
∑
n
=
0
∞
p
2
n
z
4
n
+
1
(
4
n
+
1
)
!
,
|
z
|
<
ϖ
2
{\displaystyle \operatorname {sl} z=\sum _{n=0}^{\infty }p_{2n}{\frac {z^{4n+1}}{(4n+1)!}},\quad \left|z\right|<{\frac {\varpi }{\sqrt {2}}}}
where
p
n
+
2
=
−
12
∑
j
=
0
n
(
2
n
+
2
2
j
+
2
)
p
n
−
j
∑
k
=
0
j
(
2
j
+
1
2
k
+
1
)
p
k
p
j
−
k
,
p
0
=
1
,
p
1
=
0.
{\displaystyle p_{n+2}=-12\sum _{j=0}^{n}{\binom {2n+2}{2j+2}}p_{n-j}\sum _{k=0}^{j}{\binom {2j+1}{2k+1}}p_{k}p_{j-k},\quad p_{0}=1,\,p_{1}=0.}
The power series expansion of
sl
~
{\displaystyle {\tilde {\operatorname {sl} }}}
sl
~
z
=
∑
n
=
0
∞
α
n
z
n
=
z
−
9
z
3
3
!
+
153
z
5
5
!
−
4977
z
7
7
!
+
⋯
,
|
z
|
<
ϖ
2
{\displaystyle {\tilde {\operatorname {sl} }}\,z=\sum _{n=0}^{\infty }\alpha _{n}z^{n}=z-9{\frac {z^{3}}{3!}}+153{\frac {z^{5}}{5!}}-4977{\frac {z^{7}}{7!}}+\cdots ,\quad \left|z\right|<{\frac {\varpi }{2}}}
where
α
n
=
0
{\displaystyle \alpha _{n}=0}
n
{\displaystyle n}
[ 39]
α
n
=
2
π
ϖ
(
−
1
)
(
n
−
1
)
/
2
n
!
∑
k
=
1
∞
(
2
k
π
/
ϖ
)
n
+
1
cosh
k
π
,
|
α
n
|
∼
2
n
+
5
/
2
n
+
1
ϖ
n
+
2
{\displaystyle \alpha _{n}={\sqrt {2}}{\frac {\pi }{\varpi }}{\frac {(-1)^{(n-1)/2}}{n!}}\sum _{k=1}^{\infty }{\frac {(2k\pi /\varpi )^{n+1}}{\cosh k\pi }},\quad \left|\alpha _{n}\right|\sim 2^{n+5/2}{\frac {n+1}{\varpi ^{n+2}}}}
if
n
{\displaystyle n}
The expansion can be equivalently written as[ 40]
sl
~
z
=
∑
n
=
0
∞
(
−
1
)
n
2
n
+
1
(
∑
l
=
0
n
2
l
(
2
n
+
2
2
l
+
1
)
s
l
t
n
−
l
)
z
2
n
+
1
(
2
n
+
1
)
!
,
|
z
|
<
ϖ
2
{\displaystyle {\tilde {\operatorname {sl} }}\,z=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2^{n+1}}}\left(\sum _{l=0}^{n}2^{l}{\binom {2n+2}{2l+1}}s_{l}t_{n-l}\right){\frac {z^{2n+1}}{(2n+1)!}},\quad \left|z\right|<{\frac {\varpi }{2}}}
where
s
n
+
2
=
3
s
n
+
1
+
24
∑
j
=
0
n
(
2
n
+
2
2
j
+
2
)
s
n
−
j
∑
k
=
0
j
(
2
j
+
1
2
k
+
1
)
s
k
s
j
−
k
,
s
0
=
1
,
s
1
=
3
,
{\displaystyle s_{n+2}=3s_{n+1}+24\sum _{j=0}^{n}{\binom {2n+2}{2j+2}}s_{n-j}\sum _{k=0}^{j}{\binom {2j+1}{2k+1}}s_{k}s_{j-k},\quad s_{0}=1,\,s_{1}=3,}
t
n
+
2
=
3
t
n
+
1
+
3
∑
j
=
0
n
(
2
n
+
2
2
j
+
2
)
t
n
−
j
∑
k
=
0
j
(
2
j
+
1
2
k
+
1
)
t
k
t
j
−
k
,
t
0
=
1
,
t
1
=
3.
{\displaystyle t_{n+2}=3t_{n+1}+3\sum _{j=0}^{n}{\binom {2n+2}{2j+2}}t_{n-j}\sum _{k=0}^{j}{\binom {2j+1}{2k+1}}t_{k}t_{j-k},\quad t_{0}=1,\,t_{1}=3.}
For the lemniscate cosine,[ 41]
cl
z
=
1
−
∑
n
=
0
∞
(
−
1
)
n
(
∑
l
=
0
n
2
l
(
2
n
+
2
2
l
+
1
)
q
l
r
n
−
l
)
z
2
n
+
2
(
2
n
+
2
)
!
=
1
−
2
z
2
2
!
+
12
z
4
4
!
−
216
z
6
6
!
+
⋯
,
|
z
|
<
ϖ
2
,
{\displaystyle \operatorname {cl} {z}=1-\sum _{n=0}^{\infty }(-1)^{n}\left(\sum _{l=0}^{n}2^{l}{\binom {2n+2}{2l+1}}q_{l}r_{n-l}\right){\frac {z^{2n+2}}{(2n+2)!}}=1-2{\frac {z^{2}}{2!}}+12{\frac {z^{4}}{4!}}-216{\frac {z^{6}}{6!}}+\cdots ,\quad \left|z\right|<{\frac {\varpi }{2}},}
cl
~
z
=
∑
n
=
0
∞
(
−
1
)
n
2
n
q
n
z
2
n
(
2
n
)
!
=
1
−
3
z
2
2
!
+
33
z
4
4
!
−
819
z
6
6
!
+
⋯
,
|
z
|
<
ϖ
2
{\displaystyle {\tilde {\operatorname {cl} }}\,z=\sum _{n=0}^{\infty }(-1)^{n}2^{n}q_{n}{\frac {z^{2n}}{(2n)!}}=1-3{\frac {z^{2}}{2!}}+33{\frac {z^{4}}{4!}}-819{\frac {z^{6}}{6!}}+\cdots ,\quad \left|z\right|<{\frac {\varpi }{2}}}
where
r
n
+
2
=
3
∑
j
=
0
n
(
2
n
+
2
2
j
+
2
)
r
n
−
j
∑
k
=
0
j
(
2
j
+
1
2
k
+
1
)
r
k
r
j
−
k
,
r
0
=
1
,
r
1
=
0
,
{\displaystyle r_{n+2}=3\sum _{j=0}^{n}{\binom {2n+2}{2j+2}}r_{n-j}\sum _{k=0}^{j}{\binom {2j+1}{2k+1}}r_{k}r_{j-k},\quad r_{0}=1,\,r_{1}=0,}
q
n
+
2
=
3
2
q
n
+
1
+
6
∑
j
=
0
n
(
2
n
+
2
2
j
+
2
)
q
n
−
j
∑
k
=
0
j
(
2
j
+
1
2
k
+
1
)
q
k
q
j
−
k
,
q
0
=
1
,
q
1
=
3
2
.
{\displaystyle q_{n+2}={\tfrac {3}{2}}q_{n+1}+6\sum _{j=0}^{n}{\binom {2n+2}{2j+2}}q_{n-j}\sum _{k=0}^{j}{\binom {2j+1}{2k+1}}q_{k}q_{j-k},\quad q_{0}=1,\,q_{1}={\tfrac {3}{2}}.}
Ramanujan's famous cos/cosh identity states that if
R
(
s
)
=
π
ϖ
2
∑
n
∈
Z
cos
(
2
n
π
s
/
ϖ
)
cosh
n
π
,
{\displaystyle R(s)={\frac {\pi }{\varpi {\sqrt {2}}}}\sum _{n\in \mathbb {Z} }{\frac {\cos(2n\pi s/\varpi )}{\cosh n\pi }},}
then[ 39]
R
(
s
)
−
2
+
R
(
i
s
)
−
2
=
2
,
|
Re
s
|
<
ϖ
2
,
|
Im
s
|
<
ϖ
2
.
{\displaystyle R(s)^{-2}+R(is)^{-2}=2,\quad \left|\operatorname {Re} s\right|<{\frac {\varpi }{2}},\left|\operatorname {Im} s\right|<{\frac {\varpi }{2}}.}
There is a close relation between the lemniscate functions and
R
(
s
)
{\displaystyle R(s)}
[ 39] [ 42]
sl
~
s
=
−
d
d
s
R
(
s
)
|
Im
s
|
<
ϖ
2
{\displaystyle {\tilde {\operatorname {sl} }}\,s=-{\frac {\mathrm {d} }{\mathrm {d} s}}R(s)\quad \left|\operatorname {Im} s\right|<{\frac {\varpi }{2}}}
cl
~
s
=
d
d
s
1
−
R
(
s
)
2
,
|
Re
s
−
ϖ
2
|
<
ϖ
2
,
|
Im
s
|
<
ϖ
2
{\displaystyle {\tilde {\operatorname {cl} }}\,s={\frac {\mathrm {d} }{\mathrm {d} s}}{\sqrt {1-R(s)^{2}}},\quad \left|\operatorname {Re} s-{\frac {\varpi }{2}}\right|<{\frac {\varpi }{2}},\,\left|\operatorname {Im} s\right|<{\frac {\varpi }{2}}}
and
R
(
s
)
=
1
1
+
sl
2
s
,
|
Im
s
|
<
ϖ
2
.
{\displaystyle R(s)={\frac {1}{\sqrt {1+\operatorname {sl} ^{2}s}}},\quad \left|\operatorname {Im} s\right|<{\frac {\varpi }{2}}.}
Continued fractions
For
z
∈
C
∖
{
0
}
{\displaystyle z\in \mathbb {C} \setminus \{0\}}
[ 43]
∫
0
∞
e
−
t
z
2
cl
t
d
t
=
1
/
2
z
+
a
1
z
+
a
2
z
+
a
3
z
+
⋱
,
a
n
=
n
2
4
(
(
−
1
)
n
+
1
+
3
)
{\displaystyle \int _{0}^{\infty }e^{-tz{\sqrt {2}}}\operatorname {cl} t\,\mathrm {d} t={\cfrac {1/{\sqrt {2}}}{z+{\cfrac {a_{1}}{z+{\cfrac {a_{2}}{z+{\cfrac {a_{3}}{z+\ddots }}}}}}}},\quad a_{n}={\frac {n^{2}}{4}}((-1)^{n+1}+3)}
∫
0
∞
e
−
t
z
2
sl
t
cl
t
d
t
=
1
/
2
z
2
+
b
1
−
a
1
z
2
+
b
2
−
a
2
z
2
+
b
3
−
⋱
,
a
n
=
n
2
(
4
n
2
−
1
)
,
b
n
=
3
(
2
n
−
1
)
2
{\displaystyle \int _{0}^{\infty }e^{-tz{\sqrt {2}}}\operatorname {sl} t\operatorname {cl} t\,\mathrm {d} t={\cfrac {1/2}{z^{2}+b_{1}-{\cfrac {a_{1}}{z^{2}+b_{2}-{\cfrac {a_{2}}{z^{2}+b_{3}-\ddots }}}}}},\quad a_{n}=n^{2}(4n^{2}-1),\,b_{n}=3(2n-1)^{2}}
Methods of computation
Several methods of computing
sl
x
{\displaystyle \operatorname {sl} x}
π
x
=
ϖ
x
~
{\displaystyle \pi x=\varpi {\tilde {x}}}
sl
(
ϖ
x
~
/
π
)
.
{\displaystyle \operatorname {sl} (\varpi {\tilde {x}}/\pi ).}
A hyperbolic series method:[ 46] [ 47]
sl
(
ϖ
π
x
)
=
π
ϖ
∑
n
∈
Z
(
−
1
)
n
cosh
(
x
−
(
n
+
1
/
2
)
π
)
,
x
∈
C
{\displaystyle \operatorname {sl} \left({\frac {\varpi }{\pi }}x\right)={\frac {\pi }{\varpi }}\sum _{n\in \mathbb {Z} }{\frac {(-1)^{n}}{\cosh(x-(n+1/2)\pi )}},\quad x\in \mathbb {C} }
1
sl
(
ϖ
x
/
π
)
=
π
ϖ
∑
n
∈
Z
(
−
1
)
n
sinh
(
x
−
n
π
)
=
π
ϖ
∑
n
∈
Z
(
−
1
)
n
sin
(
x
−
n
π
i
)
,
x
∈
C
{\displaystyle {\frac {1}{\operatorname {sl} (\varpi x/\pi )}}={\frac {\pi }{\varpi }}\sum _{n\in \mathbb {Z} }{\frac {(-1)^{n}}{{\sinh }{\left(x-n\pi \right)}}}={\frac {\pi }{\varpi }}\sum _{n\in \mathbb {Z} }{\frac {(-1)^{n}}{\sin(x-n\pi i)}},\quad x\in \mathbb {C} }
Fourier series method:[ 48]
sl
(
ϖ
π
x
)
=
2
π
ϖ
∑
n
=
0
∞
(
−
1
)
n
sin
(
(
2
n
+
1
)
x
)
cosh
(
(
n
+
1
/
2
)
π
)
,
|
Im
x
|
<
π
2
{\displaystyle \operatorname {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}={\frac {2\pi }{\varpi }}\sum _{n=0}^{\infty }{\frac {(-1)^{n}\sin((2n+1)x)}{\cosh((n+1/2)\pi )}},\quad \left|\operatorname {Im} x\right|<{\frac {\pi }{2}}}
cl
(
ϖ
π
x
)
=
2
π
ϖ
∑
n
=
0
∞
cos
(
(
2
n
+
1
)
x
)
cosh
(
(
n
+
1
/
2
)
π
)
,
|
Im
x
|
<
π
2
{\displaystyle \operatorname {cl} \left({\frac {\varpi }{\pi }}x\right)={\frac {2\pi }{\varpi }}\sum _{n=0}^{\infty }{\frac {\cos((2n+1)x)}{\cosh((n+1/2)\pi )}},\quad \left|\operatorname {Im} x\right|<{\frac {\pi }{2}}}
1
sl
(
ϖ
x
/
π
)
=
π
ϖ
(
1
sin
x
−
4
∑
n
=
0
∞
sin
(
(
2
n
+
1
)
x
)
e
(
2
n
+
1
)
π
+
1
)
,
|
Im
x
|
<
π
{\displaystyle {\frac {1}{\operatorname {sl} (\varpi x/\pi )}}={\frac {\pi }{\varpi }}\left({\frac {1}{\sin x}}-4\sum _{n=0}^{\infty }{\frac {\sin((2n+1)x)}{e^{(2n+1)\pi }+1}}\right),\quad \left|\operatorname {Im} x\right|<\pi }
The lemniscate functions can be computed more rapidly by
sl
(
ϖ
π
x
)
=
θ
1
(
x
,
e
−
π
)
θ
3
(
x
,
e
−
π
)
,
x
∈
C
cl
(
ϖ
π
x
)
=
θ
2
(
x
,
e
−
π
)
θ
4
(
x
,
e
−
π
)
,
x
∈
C
{\displaystyle {\begin{aligned}\operatorname {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}&={\frac {{\theta _{1}}{\left(x,e^{-\pi }\right)}}{{\theta _{3}}{\left(x,e^{-\pi }\right)}}},\quad x\in \mathbb {C} \\\operatorname {cl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}&={\frac {{\theta _{2}}{\left(x,e^{-\pi }\right)}}{{\theta _{4}}{\left(x,e^{-\pi }\right)}}},\quad x\in \mathbb {C} \end{aligned}}}
where
θ
1
(
x
,
e
−
π
)
=
∑
n
∈
Z
(
−
1
)
n
+
1
e
−
π
(
n
+
1
/
2
+
x
/
π
)
2
=
∑
n
∈
Z
(
−
1
)
n
e
−
π
(
n
+
1
/
2
)
2
sin
(
(
2
n
+
1
)
x
)
,
θ
2
(
x
,
e
−
π
)
=
∑
n
∈
Z
(
−
1
)
n
e
−
π
(
n
+
x
/
π
)
2
=
∑
n
∈
Z
e
−
π
(
n
+
1
/
2
)
2
cos
(
(
2
n
+
1
)
x
)
,
θ
3
(
x
,
e
−
π
)
=
∑
n
∈
Z
e
−
π
(
n
+
x
/
π
)
2
=
∑
n
∈
Z
e
−
π
n
2
cos
2
n
x
,
θ
4
(
x
,
e
−
π
)
=
∑
n
∈
Z
e
−
π
(
n
+
1
/
2
+
x
/
π
)
2
=
∑
n
∈
Z
(
−
1
)
n
e
−
π
n
2
cos
2
n
x
{\displaystyle {\begin{aligned}\theta _{1}(x,e^{-\pi })&=\sum _{n\in \mathbb {Z} }(-1)^{n+1}e^{-\pi (n+1/2+x/\pi )^{2}}=\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi (n+1/2)^{2}}\sin((2n+1)x),\\\theta _{2}(x,e^{-\pi })&=\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi (n+x/\pi )^{2}}=\sum _{n\in \mathbb {Z} }e^{-\pi (n+1/2)^{2}}\cos((2n+1)x),\\\theta _{3}(x,e^{-\pi })&=\sum _{n\in \mathbb {Z} }e^{-\pi (n+x/\pi )^{2}}=\sum _{n\in \mathbb {Z} }e^{-\pi n^{2}}\cos 2nx,\\\theta _{4}(x,e^{-\pi })&=\sum _{n\in \mathbb {Z} }e^{-\pi (n+1/2+x/\pi )^{2}}=\sum _{n\in \mathbb {Z} }(-1)^{n}e^{-\pi n^{2}}\cos 2nx\end{aligned}}}
are the Jacobi theta functions .[ 49]
Fourier series for the logarithm of the lemniscate sine:
ln
sl
(
ϖ
π
x
)
=
ln
2
−
π
4
+
ln
sin
x
+
2
∑
n
=
1
∞
(
−
1
)
n
cos
2
n
x
n
(
e
n
π
+
(
−
1
)
n
)
,
|
Im
x
|
<
π
2
{\displaystyle \ln \operatorname {sl} \left({\frac {\varpi }{\pi }}x\right)=\ln 2-{\frac {\pi }{4}}+\ln \sin x+2\sum _{n=1}^{\infty }{\frac {(-1)^{n}\cos 2nx}{n(e^{n\pi }+(-1)^{n})}},\quad \left|\operatorname {Im} x\right|<{\frac {\pi }{2}}}
The following series identities were discovered by Ramanujan :[ 50]
ϖ
2
π
2
sl
2
(
ϖ
x
/
π
)
=
1
sin
2
x
−
1
π
−
8
∑
n
=
1
∞
n
cos
2
n
x
e
2
n
π
−
1
,
|
Im
x
|
<
π
{\displaystyle {\frac {\varpi ^{2}}{\pi ^{2}\operatorname {sl} ^{2}(\varpi x/\pi )}}={\frac {1}{\sin ^{2}x}}-{\frac {1}{\pi }}-8\sum _{n=1}^{\infty }{\frac {n\cos 2nx}{e^{2n\pi }-1}},\quad \left|\operatorname {Im} x\right|<\pi }
arctan
sl
(
ϖ
π
x
)
=
2
∑
n
=
0
∞
sin
(
(
2
n
+
1
)
x
)
(
2
n
+
1
)
cosh
(
(
n
+
1
/
2
)
π
)
,
|
Im
x
|
<
π
2
{\displaystyle \arctan \operatorname {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=2\sum _{n=0}^{\infty }{\frac {\sin((2n+1)x)}{(2n+1)\cosh((n+1/2)\pi )}},\quad \left|\operatorname {Im} x\right|<{\frac {\pi }{2}}}
The functions
sl
~
{\displaystyle {\tilde {\operatorname {sl} }}}
cl
~
{\displaystyle {\tilde {\operatorname {cl} }}}
sin
{\displaystyle \sin }
cos
{\displaystyle \cos }
[ 39] [ 42] [ 51]
sl
~
s
=
2
2
π
2
ϖ
2
∑
n
=
1
∞
n
sin
(
2
n
π
s
/
ϖ
)
cosh
n
π
,
|
Im
s
|
<
ϖ
2
{\displaystyle {\tilde {\operatorname {sl} }}\,s=2{\sqrt {2}}{\frac {\pi ^{2}}{\varpi ^{2}}}\sum _{n=1}^{\infty }{\frac {n\sin(2n\pi s/\varpi )}{\cosh n\pi }},\quad \left|\operatorname {Im} s\right|<{\frac {\varpi }{2}}}
cl
~
s
=
2
π
2
ϖ
2
∑
n
=
0
∞
(
2
n
+
1
)
cos
(
(
2
n
+
1
)
π
s
/
ϖ
)
sinh
(
(
n
+
1
/
2
)
π
)
,
|
Im
s
|
<
ϖ
2
{\displaystyle {\tilde {\operatorname {cl} }}\,s={\sqrt {2}}{\frac {\pi ^{2}}{\varpi ^{2}}}\sum _{n=0}^{\infty }{\frac {(2n+1)\cos((2n+1)\pi s/\varpi )}{\sinh((n+1/2)\pi )}},\quad \left|\operatorname {Im} s\right|<{\frac {\varpi }{2}}}
sl
~
s
=
π
2
ϖ
2
2
∑
n
∈
Z
sinh
(
π
(
n
+
s
/
ϖ
)
)
cosh
2
(
π
(
n
+
s
/
ϖ
)
)
,
s
∈
C
{\displaystyle {\tilde {\operatorname {sl} }}\,s={\frac {\pi ^{2}}{\varpi ^{2}{\sqrt {2}}}}\sum _{n\in \mathbb {Z} }{\frac {\sinh(\pi (n+s/\varpi ))}{\cosh ^{2}(\pi (n+s/\varpi ))}},\quad s\in \mathbb {C} }
cl
~
s
=
π
2
ϖ
2
2
∑
n
∈
Z
(
−
1
)
n
cosh
2
(
π
(
n
+
s
/
ϖ
)
)
,
s
∈
C
{\displaystyle {\tilde {\operatorname {cl} }}\,s={\frac {\pi ^{2}}{\varpi ^{2}{\sqrt {2}}}}\sum _{n\in \mathbb {Z} }{\frac {(-1)^{n}}{\cosh ^{2}(\pi (n+s/\varpi ))}},\quad s\in \mathbb {C} }
The following identities come from product representations of the theta functions:[ 52]
s
l
(
ϖ
π
x
)
=
2
e
−
π
/
4
sin
x
∏
n
=
1
∞
1
−
2
e
−
2
n
π
cos
2
x
+
e
−
4
n
π
1
+
2
e
−
(
2
n
−
1
)
π
cos
2
x
+
e
−
(
4
n
−
2
)
π
,
x
∈
C
{\displaystyle \mathrm {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=2e^{-\pi /4}\sin x\prod _{n=1}^{\infty }{\frac {1-2e^{-2n\pi }\cos 2x+e^{-4n\pi }}{1+2e^{-(2n-1)\pi }\cos 2x+e^{-(4n-2)\pi }}},\quad x\in \mathbb {C} }
c
l
(
ϖ
π
x
)
=
2
e
−
π
/
4
cos
x
∏
n
=
1
∞
1
+
2
e
−
2
n
π
cos
2
x
+
e
−
4
n
π
1
−
2
e
−
(
2
n
−
1
)
π
cos
2
x
+
e
−
(
4
n
−
2
)
π
,
x
∈
C
{\displaystyle \mathrm {cl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=2e^{-\pi /4}\cos x\prod _{n=1}^{\infty }{\frac {1+2e^{-2n\pi }\cos 2x+e^{-4n\pi }}{1-2e^{-(2n-1)\pi }\cos 2x+e^{-(4n-2)\pi }}},\quad x\in \mathbb {C} }
A similar formula involving the
sn
{\displaystyle \operatorname {sn} }
[ 53]
The lemniscate functions as a ratio of entire functions
Since the lemniscate sine is a meromorphic function in the whole complex plane, it can be written as a ratio of entire functions . Gauss showed that sl has the following product expansion, reflecting the distribution of its zeros and poles:[ 54]
sl
z
=
M
(
z
)
N
(
z
)
{\displaystyle \operatorname {sl} z={\frac {M(z)}{N(z)}}}
where
M
(
z
)
=
z
∏
α
(
1
−
z
4
α
4
)
,
N
(
z
)
=
∏
β
(
1
−
z
4
β
4
)
.
{\displaystyle M(z)=z\prod _{\alpha }\left(1-{\frac {z^{4}}{\alpha ^{4}}}\right),\quad N(z)=\prod _{\beta }\left(1-{\frac {z^{4}}{\beta ^{4}}}\right).}
Here,
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
sl which are in the quadrant
Re
z
>
0
,
Im
z
≥
0
{\displaystyle \operatorname {Re} z>0,\operatorname {Im} z\geq 0}
[ 54] [ 55] uniform convergence .[ 56]
Proof of the infinite product for the lemniscate sine
Proof by logarithmic differentiation
It can be easily seen (using uniform and absolute convergence arguments to justify interchanging of limiting operations ) that
M
′
(
z
)
M
(
z
)
=
−
∑
n
=
0
∞
2
4
n
H
4
n
z
4
n
−
1
(
4
n
)
!
,
|
z
|
<
ϖ
{\displaystyle {\frac {M'(z)}{M(z)}}=-\sum _{n=0}^{\infty }2^{4n}\mathrm {H} _{4n}{\frac {z^{4n-1}}{(4n)!}},\quad \left|z\right|<\varpi }
(where
H
n
{\displaystyle \mathrm {H} _{n}}
Lemniscate elliptic functions § Hurwitz numbers ) and
N
′
(
z
)
N
(
z
)
=
(
1
+
i
)
M
′
(
(
1
+
i
)
z
)
M
(
(
1
+
i
)
z
)
−
M
′
(
z
)
M
(
z
)
.
{\displaystyle {\frac {N'(z)}{N(z)}}=(1+i){\frac {M'((1+i)z)}{M((1+i)z)}}-{\frac {M'(z)}{M(z)}}.}
Therefore
N
′
(
z
)
N
(
z
)
=
∑
n
=
0
∞
2
4
n
(
1
−
(
−
1
)
n
2
2
n
)
H
4
n
z
4
n
−
1
(
4
n
)
!
,
|
z
|
<
ϖ
2
.
{\displaystyle {\frac {N'(z)}{N(z)}}=\sum _{n=0}^{\infty }2^{4n}(1-(-1)^{n}2^{2n})\mathrm {H} _{4n}{\frac {z^{4n-1}}{(4n)!}},\quad \left|z\right|<{\frac {\varpi }{\sqrt {2}}}.}
It is known that
1
sl
2
z
=
∑
n
=
0
∞
2
4
n
(
4
n
−
1
)
H
4
n
z
4
n
−
2
(
4
n
)
!
,
|
z
|
<
ϖ
.
{\displaystyle {\frac {1}{\operatorname {sl} ^{2}z}}=\sum _{n=0}^{\infty }2^{4n}(4n-1)\mathrm {H} _{4n}{\frac {z^{4n-2}}{(4n)!}},\quad \left|z\right|<\varpi .}
Then from
d
d
z
sl
′
z
sl
z
=
−
1
sl
2
z
−
sl
2
z
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}{\frac {\operatorname {sl} 'z}{\operatorname {sl} z}}=-{\frac {1}{\operatorname {sl} ^{2}z}}-\operatorname {sl} ^{2}z}
and
sl
2
z
=
1
sl
2
z
−
(
1
+
i
)
2
sl
2
(
(
1
+
i
)
z
)
{\displaystyle \operatorname {sl} ^{2}z={\frac {1}{\operatorname {sl} ^{2}z}}-{\frac {(1+i)^{2}}{\operatorname {sl} ^{2}((1+i)z)}}}
we get
sl
′
z
sl
z
=
−
∑
n
=
0
∞
2
4
n
(
2
−
(
−
1
)
n
2
2
n
)
H
4
n
z
4
n
−
1
(
4
n
)
!
,
|
z
|
<
ϖ
2
.
{\displaystyle {\frac {\operatorname {sl} 'z}{\operatorname {sl} z}}=-\sum _{n=0}^{\infty }2^{4n}(2-(-1)^{n}2^{2n})\mathrm {H} _{4n}{\frac {z^{4n-1}}{(4n)!}},\quad \left|z\right|<{\frac {\varpi }{\sqrt {2}}}.}
Hence
sl
′
z
sl
z
=
M
′
(
z
)
M
(
z
)
−
N
′
(
z
)
N
(
z
)
,
|
z
|
<
ϖ
2
.
{\displaystyle {\frac {\operatorname {sl} 'z}{\operatorname {sl} z}}={\frac {M'(z)}{M(z)}}-{\frac {N'(z)}{N(z)}},\quad \left|z\right|<{\frac {\varpi }{\sqrt {2}}}.}
Therefore
sl
z
=
C
M
(
z
)
N
(
z
)
{\displaystyle \operatorname {sl} z=C{\frac {M(z)}{N(z)}}}
for some constant
C
{\displaystyle C}
|
z
|
<
ϖ
/
2
{\displaystyle \left|z\right|<\varpi /{\sqrt {2}}}
z
∈
C
{\displaystyle z\in \mathbb {C} }
lim
z
→
0
sl
z
z
=
1
{\displaystyle \lim _{z\to 0}{\frac {\operatorname {sl} z}{z}}=1}
gives
C
=
1
{\displaystyle C=1}
◼
{\displaystyle \blacksquare }
Proof by Liouville's theorem
Let
f
(
z
)
=
M
(
z
)
N
(
z
)
=
(
1
+
i
)
M
(
z
)
2
M
(
(
1
+
i
)
z
)
,
{\displaystyle f(z)={\frac {M(z)}{N(z)}}={\frac {(1+i)M(z)^{2}}{M((1+i)z)}},}
with patches at removable singularities.
The shifting formulas
M
(
z
+
2
ϖ
)
=
e
2
π
ϖ
(
z
+
ϖ
)
M
(
z
)
,
M
(
z
+
2
ϖ
i
)
=
e
−
2
π
ϖ
(
i
z
−
ϖ
)
M
(
z
)
{\displaystyle M(z+2\varpi )=e^{2{\frac {\pi }{\varpi }}(z+\varpi )}M(z),\quad M(z+2\varpi i)=e^{-2{\frac {\pi }{\varpi }}(iz-\varpi )}M(z)}
imply that
f
{\displaystyle f}
2
ϖ
{\displaystyle 2\varpi }
2
ϖ
i
{\displaystyle 2\varpi i}
sl
{\displaystyle \operatorname {sl} }
g
{\displaystyle g}
g
(
z
)
=
sl
z
f
(
z
)
,
{\displaystyle g(z)={\frac {\operatorname {sl} z}{f(z)}},}
when patched, is an elliptic function without poles. By Liouville's theorem , it is a constant. By using
sl
z
=
z
+
O
(
z
5
)
{\displaystyle \operatorname {sl} z=z+\operatorname {O} (z^{5})}
M
(
z
)
=
z
+
O
(
z
5
)
{\displaystyle M(z)=z+\operatorname {O} (z^{5})}
N
(
z
)
=
1
+
O
(
z
4
)
{\displaystyle N(z)=1+\operatorname {O} (z^{4})}
1
{\displaystyle 1}
◼
{\displaystyle \blacksquare }
Gauss conjectured that
ln
N
(
ϖ
)
=
π
/
2
{\displaystyle \ln N(\varpi )=\pi /2}
[ 57]
M
{\displaystyle M}
N
{\displaystyle N}
M
{\displaystyle M}
N
{\displaystyle N}
The
M
{\displaystyle M}
The
N
{\displaystyle N}
N
(
z
)
=
M
(
(
1
+
i
)
z
)
(
1
+
i
)
M
(
z
)
,
z
∉
ϖ
Z
[
i
]
{\displaystyle N(z)={\frac {M((1+i)z)}{(1+i)M(z)}},\quad z\notin \varpi \mathbb {Z} [i]}
and
N
(
2
z
)
=
M
(
z
)
4
+
N
(
z
)
4
.
{\displaystyle N(2z)=M(z)^{4}+N(z)^{4}.}
Thanks to a certain theorem[ 58]
z
{\displaystyle z}
[ 59] [ 60] [ 61] [ 62] [ 63]
M
(
z
)
=
z
−
2
z
5
5
!
−
36
z
9
9
!
+
552
z
13
13
!
+
⋯
,
z
∈
C
{\displaystyle M(z)=z-2{\frac {z^{5}}{5!}}-36{\frac {z^{9}}{9!}}+552{\frac {z^{13}}{13!}}+\cdots ,\quad z\in \mathbb {C} }
N
(
z
)
=
1
+
2
z
4
4
!
−
4
z
8
8
!
+
408
z
12
12
!
+
⋯
,
z
∈
C
.
{\displaystyle N(z)=1+2{\frac {z^{4}}{4!}}-4{\frac {z^{8}}{8!}}+408{\frac {z^{12}}{12!}}+\cdots ,\quad z\in \mathbb {C} .}
This can be contrasted with the power series of
sl
{\displaystyle \operatorname {sl} }
We define
S
{\displaystyle S}
T
{\displaystyle T}
S
(
z
)
=
N
(
z
1
+
i
)
2
−
i
M
(
z
1
+
i
)
2
,
T
(
z
)
=
S
(
i
z
)
.
{\displaystyle S(z)=N\left({\frac {z}{1+i}}\right)^{2}-iM\left({\frac {z}{1+i}}\right)^{2},\quad T(z)=S(iz).}
Then the lemniscate cosine can be written as
cl
z
=
S
(
z
)
T
(
z
)
{\displaystyle \operatorname {cl} z={\frac {S(z)}{T(z)}}}
where[ 64]
S
(
z
)
=
1
−
z
2
2
!
−
z
4
4
!
−
3
z
6
6
!
+
17
z
8
8
!
−
9
z
10
10
!
+
111
z
12
12
!
+
⋯
,
z
∈
C
{\displaystyle S(z)=1-{\frac {z^{2}}{2!}}-{\frac {z^{4}}{4!}}-3{\frac {z^{6}}{6!}}+17{\frac {z^{8}}{8!}}-9{\frac {z^{10}}{10!}}+111{\frac {z^{12}}{12!}}+\cdots ,\quad z\in \mathbb {C} }
T
(
z
)
=
1
+
z
2
2
!
−
z
4
4
!
+
3
z
6
6
!
+
17
z
8
8
!
+
9
z
10
10
!
+
111
z
12
12
!
+
⋯
,
z
∈
C
.
{\displaystyle T(z)=1+{\frac {z^{2}}{2!}}-{\frac {z^{4}}{4!}}+3{\frac {z^{6}}{6!}}+17{\frac {z^{8}}{8!}}+9{\frac {z^{10}}{10!}}+111{\frac {z^{12}}{12!}}+\cdots ,\quad z\in \mathbb {C} .}
Furthermore, the identities
M
(
2
z
)
=
2
M
(
z
)
N
(
z
)
S
(
z
)
T
(
z
)
,
{\displaystyle M(2z)=2M(z)N(z)S(z)T(z),}
S
(
2
z
)
=
S
(
z
)
4
−
2
M
(
z
)
4
,
{\displaystyle S(2z)=S(z)^{4}-2M(z)^{4},}
T
(
2
z
)
=
T
(
z
)
4
−
2
M
(
z
)
4
{\displaystyle T(2z)=T(z)^{4}-2M(z)^{4}}
and the Pythagorean-like identities
M
(
z
)
2
+
S
(
z
)
2
=
N
(
z
)
2
,
{\displaystyle M(z)^{2}+S(z)^{2}=N(z)^{2},}
M
(
z
)
2
+
N
(
z
)
2
=
T
(
z
)
2
{\displaystyle M(z)^{2}+N(z)^{2}=T(z)^{2}}
hold for all
z
∈
C
{\displaystyle z\in \mathbb {C} }
The quasi-addition formulas
M
(
z
+
w
)
M
(
z
−
w
)
=
M
(
z
)
2
N
(
w
)
2
−
N
(
z
)
2
M
(
w
)
2
,
{\displaystyle M(z+w)M(z-w)=M(z)^{2}N(w)^{2}-N(z)^{2}M(w)^{2},}
N
(
z
+
w
)
N
(
z
−
w
)
=
N
(
z
)
2
N
(
w
)
2
+
M
(
z
)
2
M
(
w
)
2
{\displaystyle N(z+w)N(z-w)=N(z)^{2}N(w)^{2}+M(z)^{2}M(w)^{2}}
(where
z
,
w
∈
C
{\displaystyle z,w\in \mathbb {C} }
M
{\displaystyle M}
N
{\displaystyle N}
[ 65]
Gauss'
M
{\displaystyle M}
N
{\displaystyle N}
M
(
z
)
M
″
(
z
)
=
M
′
(
z
)
2
−
N
(
z
)
2
,
{\displaystyle M(z)M''(z)=M'(z)^{2}-N(z)^{2},}
N
(
z
)
N
″
(
z
)
=
N
′
(
z
)
2
+
M
(
z
)
2
{\displaystyle N(z)N''(z)=N'(z)^{2}+M(z)^{2}}
where
z
∈
C
{\displaystyle z\in \mathbb {C} }
M
{\displaystyle M}
N
{\displaystyle N}
[ 66]
X
(
z
)
X
⁗
(
z
)
=
4
X
′
(
z
)
X
‴
(
z
)
−
3
X
″
(
z
)
2
+
2
X
(
z
)
2
,
z
∈
C
.
{\displaystyle X(z)X''''(z)=4X'(z)X'''(z)-3X''(z)^{2}+2X(z)^{2},\quad z\in \mathbb {C} .}
The functions can be also expressed by integrals involving elliptic functions:
M
(
z
)
=
z
exp
(
−
∫
0
z
∫
0
w
(
1
sl
2
v
−
1
v
2
)
d
v
d
w
)
,
{\displaystyle M(z)=z\exp \left(-\int _{0}^{z}\int _{0}^{w}\left({\frac {1}{\operatorname {sl} ^{2}v}}-{\frac {1}{v^{2}}}\right)\,\mathrm {d} v\,\mathrm {d} w\right),}
N
(
z
)
=
exp
(
∫
0
z
∫
0
w
sl
2
v
d
v
d
w
)
{\displaystyle N(z)=\exp \left(\int _{0}^{z}\int _{0}^{w}\operatorname {sl} ^{2}v\,\mathrm {d} v\,\mathrm {d} w\right)}
where the contours do not cross the poles; while the innermost integrals are path-independent, the outermost ones are path-dependent; however, the path dependence cancels out with the non-injectivity of the complex exponential function .
An alternative way of expressing the lemniscate functions as a ratio of entire functions involves the theta functions (see Lemniscate elliptic functions § Methods of computation ); the relation between
M
,
N
{\displaystyle M,N}
θ
1
,
θ
3
{\displaystyle \theta _{1},\theta _{3}}
M
(
z
)
=
2
−
1
/
4
e
π
z
2
/
(
2
ϖ
2
)
π
ϖ
θ
1
(
π
z
ϖ
,
e
−
π
)
,
{\displaystyle M(z)=2^{-1/4}e^{\pi z^{2}/(2\varpi ^{2})}{\sqrt {\frac {\pi }{\varpi }}}\theta _{1}\left({\frac {\pi z}{\varpi }},e^{-\pi }\right),}
N
(
z
)
=
2
−
1
/
4
e
π
z
2
/
(
2
ϖ
2
)
π
ϖ
θ
3
(
π
z
ϖ
,
e
−
π
)
{\displaystyle N(z)=2^{-1/4}e^{\pi z^{2}/(2\varpi ^{2})}{\sqrt {\frac {\pi }{\varpi }}}\theta _{3}\left({\frac {\pi z}{\varpi }},e^{-\pi }\right)}
where
z
∈
C
{\displaystyle z\in \mathbb {C} }
Relation to other functions
Relation to Weierstrass and Jacobi elliptic functions
The lemniscate functions are closely related to the Weierstrass elliptic function
℘
(
z
;
1
,
0
)
{\displaystyle \wp (z;1,0)}
g
2
=
1
{\displaystyle g_{2}=1}
and
g
3
=
0
{\displaystyle g_{3}=0}
. This lattice has fundamental periods
ω
1
=
2
ϖ
,
{\displaystyle \omega _{1}={\sqrt {2}}\varpi ,}
ω
2
=
i
ω
1
{\displaystyle \omega _{2}=i\omega _{1}}
e
1
=
1
2
,
e
2
=
0
,
e
3
=
−
1
2
.
{\displaystyle e_{1}={\tfrac {1}{2}},\ e_{2}=0,\ e_{3}=-{\tfrac {1}{2}}.}
The related case of a Weierstrass elliptic function with
g
2
=
a
{\displaystyle g_{2}=a}
,
g
3
=
0
{\displaystyle g_{3}=0}
may be handled by a scaling transformation. However, this may involve complex numbers. If it is desired to remain within real numbers, there are two cases to consider:
a
>
0
{\displaystyle a>0}
and
a
<
0
{\displaystyle a<0}
. The period parallelogram is either a square or a rhombus . The Weierstrass elliptic function
℘
(
z
;
−
1
,
0
)
{\displaystyle \wp (z;-1,0)}
[ 67]
The square of the lemniscate sine can be represented as
sl
2
z
=
1
℘
(
z
;
4
,
0
)
=
i
2
℘
(
(
1
−
i
)
z
;
−
1
,
0
)
=
−
2
℘
(
2
z
+
(
i
−
1
)
ϖ
2
;
1
,
0
)
{\displaystyle \operatorname {sl} ^{2}z={\frac {1}{\wp (z;4,0)}}={\frac {i}{2\wp ((1-i)z;-1,0)}}={-2\wp }{\left({\sqrt {2}}z+(i-1){\frac {\varpi }{\sqrt {2}}};1,0\right)}}
where the second and third argument of
℘
{\displaystyle \wp }
g
2
{\displaystyle g_{2}}
and
g
3
{\displaystyle g_{3}}
. The lemniscate sine is a rational function in the Weierstrass elliptic function and its derivative:[ 68]
sl
z
=
−
2
℘
(
z
;
−
1
,
0
)
℘
′
(
z
;
−
1
,
0
)
.
{\displaystyle \operatorname {sl} z=-2{\frac {\wp (z;-1,0)}{\wp '(z;-1,0)}}.}
The lemniscate functions can also be written in terms of Jacobi elliptic functions . The Jacobi elliptic functions
sn
{\displaystyle \operatorname {sn} }
cd
{\displaystyle \operatorname {cd} }
sn
{\displaystyle \operatorname {sn} }
cd
{\displaystyle \operatorname {cd} }
i
{\displaystyle i}
(and
sd
{\displaystyle \operatorname {sd} }
cn
{\displaystyle \operatorname {cn} }
1
/
2
{\displaystyle 1/{\sqrt {2}}}
[ 69] [ 70]
sl
z
=
sn
(
z
;
i
)
=
sc
(
z
;
2
)
=
1
2
sd
(
2
z
;
1
2
)
{\displaystyle \operatorname {sl} z=\operatorname {sn} (z;i)=\operatorname {sc} (z;{\sqrt {2}})={{\tfrac {1}{\sqrt {2}}}\operatorname {sd} }\left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right)}
cl
z
=
cd
(
z
;
i
)
=
dn
(
z
;
2
)
=
cn
(
2
z
;
1
2
)
{\displaystyle \operatorname {cl} z=\operatorname {cd} (z;i)=\operatorname {dn} (z;{\sqrt {2}})={\operatorname {cn} }\left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right)}
where the second arguments denote the elliptic modulus
k
{\displaystyle k}
The functions
sl
~
{\displaystyle {\tilde {\operatorname {sl} }}}
cl
~
{\displaystyle {\tilde {\operatorname {cl} }}}
sl
~
z
=
cd
(
z
;
i
)
sd
(
z
;
i
)
=
dn
(
z
;
2
)
sn
(
z
;
2
)
=
1
2
cn
(
2
z
;
1
2
)
sn
(
2
z
;
1
2
)
,
{\displaystyle {\tilde {\operatorname {sl} }}\,z=\operatorname {cd} (z;i)\operatorname {sd} (z;i)=\operatorname {dn} (z;{\sqrt {2}})\operatorname {sn} (z;{\sqrt {2}})={\tfrac {1}{\sqrt {2}}}\operatorname {cn} \left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right)\operatorname {sn} \left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right),}
cl
~
z
=
cd
(
z
;
i
)
nd
(
z
;
i
)
=
dn
(
z
;
2
)
cn
(
z
;
2
)
=
cn
(
2
z
;
1
2
)
dn
(
2
z
;
1
2
)
.
{\displaystyle {\tilde {\operatorname {cl} }}\,z=\operatorname {cd} (z;i)\operatorname {nd} (z;i)=\operatorname {dn} (z;{\sqrt {2}})\operatorname {cn} (z;{\sqrt {2}})=\operatorname {cn} \left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right)\operatorname {dn} \left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right).}
Relation to the modular lambda function
The lemniscate sine can be used for the computation of values of the modular lambda function :
∏
k
=
1
n
sl
(
2
k
−
1
2
n
+
1
ϖ
2
)
=
λ
(
(
2
n
+
1
)
i
)
1
−
λ
(
(
2
n
+
1
)
i
)
8
{\displaystyle \prod _{k=1}^{n}\;{\operatorname {sl} }{\left({\frac {2k-1}{2n+1}}{\frac {\varpi }{2}}\right)}={\sqrt[{8}]{\frac {\lambda ((2n+1)i)}{1-\lambda ((2n+1)i)}}}}
For example:
sl
(
1
14
ϖ
)
sl
(
3
14
ϖ
)
sl
(
5
14
ϖ
)
=
λ
(
7
i
)
1
−
λ
(
7
i
)
8
=
tan
(
1
2
arccsc
(
1
2
8
7
+
21
+
1
2
7
+
1
)
)
=
2
2
+
7
+
21
+
8
7
+
2
14
+
6
7
+
455
+
172
7
sl
(
1
18
ϖ
)
sl
(
3
18
ϖ
)
sl
(
5
18
ϖ
)
sl
(
7
18
ϖ
)
=
λ
(
9
i
)
1
−
λ
(
9
i
)
8
=
tan
(
|
|
π
4
−
arctan
(
|
|
2
2
3
−
2
3
−
2
2
−
3
3
+
3
−
1
12
4
|
|
)
)
{\displaystyle {\begin{aligned}&{\operatorname {sl} }{\bigl (}{\tfrac {1}{14}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {3}{14}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {5}{14}}\varpi {\bigr )}\\[7mu]&\quad {}={\sqrt[{8}]{\frac {\lambda (7i)}{1-\lambda (7i)}}}={\tan }{\Bigl (}{{\tfrac {1}{2}}\operatorname {arccsc} }{\Bigl (}{\tfrac {1}{2}}{\sqrt {8{\sqrt {7}}+21}}+{\tfrac {1}{2}}{\sqrt {7}}+1{\Bigr )}{\Bigr )}\\[7mu]&\quad {}={\frac {2}{2+{\sqrt {7}}+{\sqrt {21+8{\sqrt {7}}}}+{\sqrt {2{14+6{\sqrt {7}}+{\sqrt {455+172{\sqrt {7}}}}}}}}}\\[18mu]&{\operatorname {sl} }{\bigl (}{\tfrac {1}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {3}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {5}{18}}\varpi {\bigr )}\,{\operatorname {sl} }{\bigl (}{\tfrac {7}{18}}\varpi {\bigr )}\\&\quad {}={\sqrt[{8}]{\frac {\lambda (9i)}{1-\lambda (9i)}}}=\tan \left({\vphantom {\frac {\Big |}{\Big |}}}\right.{\frac {\pi }{4}}-\arctan \left({\vphantom {\frac {\Big |}{\Big |}}}\right.{\frac {2{\sqrt[{3}]{2{\sqrt {3}}-2}}-2{\sqrt[{3}]{2-{\sqrt {3}}}}+{\sqrt {3}}-1}{\sqrt[{4}]{12}}}\left.\left.{\vphantom {\frac {\Big |}{\Big |}}}\right)\right)\end{aligned}}}
Inverse functions
The inverse function of the lemniscate sine is the lemniscate arcsine, defined as[ 71]
arcsl
x
=
∫
0
x
d
t
1
−
t
4
.
{\displaystyle \operatorname {arcsl} x=\int _{0}^{x}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}.}
It can also be represented by the hypergeometric function :
arcsl
x
=
x
2
F
1
(
1
2
,
1
4
;
5
4
;
x
4
)
{\displaystyle \operatorname {arcsl} x=x\,{}_{2}F_{1}{\bigl (}{\tfrac {1}{2}},{\tfrac {1}{4}};{\tfrac {5}{4}};x^{4}{\bigr )}}
which can be easily seen by using the binomial series .
The inverse function of the lemniscate cosine is the lemniscate arccosine. This function is defined by following expression:
arccl
x
=
∫
x
1
d
t
1
−
t
4
=
1
2
ϖ
−
arcsl
x
{\displaystyle \operatorname {arccl} x=\int _{x}^{1}{\frac {\mathrm {d} t}{\sqrt {1-t^{4}}}}={\tfrac {1}{2}}\varpi -\operatorname {arcsl} x}
For
x
{\displaystyle x}
in the interval
−
1
≤
x
≤
1
{\displaystyle -1\leq x\leq 1}
sl
arcsl
x
=
x
{\displaystyle \operatorname {sl} \operatorname {arcsl} x=x}
cl
arccl
x
=
x
{\displaystyle \operatorname {cl} \operatorname {arccl} x=x}
For the halving of the lemniscate arc length these formulas are valid:
sl
(
1
2
arcsl
x
)
=
sin
(
1
2
arcsin
x
)
sech
(
1
2
arsinh
x
)
sl
(
1
2
arcsl
x
)
2
=
tan
(
1
4
arcsin
x
2
)
{\displaystyle {\begin{aligned}{\operatorname {sl} }{\bigl (}{\tfrac {1}{2}}\operatorname {arcsl} x{\bigr )}&={\sin }{\bigl (}{\tfrac {1}{2}}\arcsin x{\bigr )}\,{\operatorname {sech} }{\bigl (}{\tfrac {1}{2}}\operatorname {arsinh} x{\bigr )}\\{\operatorname {sl} }{\bigl (}{\tfrac {1}{2}}\operatorname {arcsl} x{\bigr )}^{2}&={\tan }{\bigl (}{\tfrac {1}{4}}\arcsin x^{2}{\bigr )}\end{aligned}}}
Furthermore there are the so called Hyperbolic lemniscate area functions:
aslh
(
x
)
=
∫
0
x
1
y
4
+
1
d
y
=
1
2
F
(
2
arctan
x
;
1
2
)
{\displaystyle \operatorname {aslh} (x)=\int _{0}^{x}{\frac {1}{\sqrt {y^{4}+1}}}\mathrm {d} y={\tfrac {1}{2}}F\left(2\arctan x;{\tfrac {1}{\sqrt {2}}}\right)}
aclh
(
x
)
=
∫
x
∞
1
y
4
+
1
d
y
=
1
2
F
(
2
arccot
x
;
1
2
)
{\displaystyle \operatorname {aclh} (x)=\int _{x}^{\infty }{\frac {1}{\sqrt {y^{4}+1}}}\mathrm {d} y={\tfrac {1}{2}}F\left(2\operatorname {arccot} x;{\tfrac {1}{\sqrt {2}}}\right)}
aclh
(
x
)
=
ϖ
2
−
aslh
(
x
)
{\displaystyle \operatorname {aclh} (x)={\frac {\varpi }{\sqrt {2}}}-\operatorname {aslh} (x)}
aslh
(
x
)
=
2
arcsl
(
x
/
1
+
x
4
+
1
)
{\displaystyle \operatorname {aslh} (x)={\sqrt {2}}\operatorname {arcsl} \left(x{\Big /}{\sqrt {\textstyle 1+{\sqrt {x^{4}+1}}}}\right)}
arcsl
(
x
)
=
2
aslh
(
x
/
1
+
1
−
x
4
)
{\displaystyle \operatorname {arcsl} (x)={\sqrt {2}}\operatorname {aslh} \left(x{\Big /}{\sqrt {\textstyle 1+{\sqrt {1-x^{4}}}}}\right)}
Expression using elliptic integrals
The lemniscate arcsine and the lemniscate arccosine can also be expressed by the Legendre-Form:
These functions can be displayed directly by using the incomplete elliptic integral of the first kind:
arcsl
x
=
1
2
F
(
arcsin
2
x
1
+
x
2
;
1
2
)
{\displaystyle \operatorname {arcsl} x={\frac {1}{\sqrt {2}}}F\left({\arcsin }{\frac {{\sqrt {2}}x}{\sqrt {1+x^{2}}}};{\frac {1}{\sqrt {2}}}\right)}
arcsl
x
=
2
(
2
−
1
)
F
(
arcsin
(
2
+
1
)
x
1
+
x
2
+
1
;
(
2
−
1
)
2
)
{\displaystyle \operatorname {arcsl} x=2({\sqrt {2}}-1)F\left({\arcsin }{\frac {({\sqrt {2}}+1)x}{{\sqrt {1+x^{2}}}+1}};({\sqrt {2}}-1)^{2}\right)}
The arc lengths of the lemniscate can also be expressed by only using the arc lengths of ellipses (calculated by elliptic integrals of the second kind):
arcsl
x
=
2
+
2
2
E
(
arcsin
(
2
+
1
)
x
1
+
x
2
+
1
;
(
2
−
1
)
2
)
−
E
(
arcsin
2
x
1
+
x
2
;
1
2
)
+
x
1
−
x
2
2
(
1
+
x
2
+
1
+
x
2
)
{\displaystyle {\begin{aligned}\operatorname {arcsl} x={}&{\frac {2+{\sqrt {2}}}{2}}E\left({\arcsin }{\frac {({\sqrt {2}}+1)x}{{\sqrt {1+x^{2}}}+1}};({\sqrt {2}}-1)^{2}\right)\\[5mu]&\ \ -E\left({\arcsin }{\frac {{\sqrt {2}}x}{\sqrt {1+x^{2}}}};{\frac {1}{\sqrt {2}}}\right)+{\frac {x{\sqrt {1-x^{2}}}}{{\sqrt {2}}(1+x^{2}+{\sqrt {1+x^{2}}})}}\end{aligned}}}
The lemniscate arccosine has this expression:
arccl
x
=
1
2
F
(
arccos
x
;
1
2
)
{\displaystyle \operatorname {arccl} x={\frac {1}{\sqrt {2}}}F\left(\arccos x;{\frac {1}{\sqrt {2}}}\right)}
Use in integration
The lemniscate arcsine can be used to integrate many functions. Here is a list of important integrals (the constants of integration are omitted):
∫
1
1
−
x
4
d
x
=
arcsl
x
{\displaystyle \int {\frac {1}{\sqrt {1-x^{4}}}}\,\mathrm {d} x=\operatorname {arcsl} x}
∫
1
(
x
2
+
1
)
(
2
x
2
+
1
)
d
x
=
arcsl
x
x
2
+
1
{\displaystyle \int {\frac {1}{\sqrt {(x^{2}+1)(2x^{2}+1)}}}\,\mathrm {d} x={\operatorname {arcsl} }{\frac {x}{\sqrt {x^{2}+1}}}}
∫
1
x
4
+
6
x
2
+
1
d
x
=
arcsl
2
x
x
4
+
6
x
2
+
1
+
x
2
+
1
{\displaystyle \int {\frac {1}{\sqrt {x^{4}+6x^{2}+1}}}\,\mathrm {d} x={\operatorname {arcsl} }{\frac {{\sqrt {2}}x}{\sqrt {{\sqrt {x^{4}+6x^{2}+1}}+x^{2}+1}}}}
∫
1
x
4
+
1
d
x
=
2
arcsl
x
x
4
+
1
+
1
{\displaystyle \int {\frac {1}{\sqrt {x^{4}+1}}}\,\mathrm {d} x={{\sqrt {2}}\operatorname {arcsl} }{\frac {x}{\sqrt {{\sqrt {x^{4}+1}}+1}}}}
∫
1
(
1
−
x
4
)
3
4
d
x
=
2
arcsl
x
1
+
1
−
x
4
{\displaystyle \int {\frac {1}{\sqrt[{4}]{(1-x^{4})^{3}}}}\,\mathrm {d} x={{\sqrt {2}}\operatorname {arcsl} }{\frac {x}{\sqrt {1+{\sqrt {1-x^{4}}}}}}}
∫
1
(
x
4
+
1
)
3
4
d
x
=
arcsl
x
x
4
+
1
4
{\displaystyle \int {\frac {1}{\sqrt[{4}]{(x^{4}+1)^{3}}}}\,\mathrm {d} x={\operatorname {arcsl} }{\frac {x}{\sqrt[{4}]{x^{4}+1}}}}
∫
1
(
1
−
x
2
)
3
4
d
x
=
2
arcsl
x
1
+
1
−
x
2
{\displaystyle \int {\frac {1}{\sqrt[{4}]{(1-x^{2})^{3}}}}\,\mathrm {d} x={2\operatorname {arcsl} }{\frac {x}{1+{\sqrt {1-x^{2}}}}}}
∫
1
(
x
2
+
1
)
3
4
d
x
=
2
arcsl
x
x
2
+
1
+
1
{\displaystyle \int {\frac {1}{\sqrt[{4}]{(x^{2}+1)^{3}}}}\,\mathrm {d} x={2\operatorname {arcsl} }{\frac {x}{{\sqrt {x^{2}+1}}+1}}}
∫
1
(
a
x
2
+
b
x
+
c
)
3
4
d
x
=
2
2
4
a
2
c
−
a
b
2
4
arcsl
2
a
x
+
b
4
a
(
a
x
2
+
b
x
+
c
)
+
4
a
c
−
b
2
{\displaystyle \int {\frac {1}{\sqrt[{4}]{(ax^{2}+bx+c)^{3}}}}\,\mathrm {d} x={{\frac {2{\sqrt {2}}}{\sqrt[{4}]{4a^{2}c-ab^{2}}}}\operatorname {arcsl} }{\frac {2ax+b}{{\sqrt {4a(ax^{2}+bx+c)}}+{\sqrt {4ac-b^{2}}}}}}
∫
sech
x
d
x
=
2
arcsl
tanh
1
2
x
{\displaystyle \int {\sqrt {\operatorname {sech} x}}\,\mathrm {d} x={2\operatorname {arcsl} }\tanh {\tfrac {1}{2}}x}
∫
sec
x
d
x
=
2
arcsl
tan
1
2
x
{\displaystyle \int {\sqrt {\sec x}}\,\mathrm {d} x={2\operatorname {arcsl} }\tan {\tfrac {1}{2}}x}
Hyperbolic lemniscate functions
The hyperbolic lemniscate sine (red) and hyperbolic lemniscate cosine (purple) applied to a real argument, in comparison with the trigonometric tangent (pale dashed red). The hyperbolic lemniscate sine in the complex plane. Dark areas represent zeros and bright areas represent poles. The complex argument is represented by varying hue. For convenience, let
σ
=
2
ϖ
{\displaystyle \sigma ={\sqrt {2}}\varpi }
σ
{\displaystyle \sigma }
π
{\displaystyle \pi }
σ
{\displaystyle \sigma }
3.7081
…
{\displaystyle 3.7081\ldots }
[ 72] [ 73]
The hyperbolic lemniscate sine (slh ) and cosine (clh ) can be defined as inverses of elliptic integrals as follows:
z
=
∗
∫
0
slh
z
d
t
1
+
t
4
=
∫
clh
z
∞
d
t
1
+
t
4
{\displaystyle z\mathrel {\overset {*}{=}} \int _{0}^{\operatorname {slh} z}{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}=\int _{\operatorname {clh} z}^{\infty }{\frac {\mathrm {d} t}{\sqrt {1+t^{4}}}}}
where in
(
∗
)
{\displaystyle (*)}
z
{\displaystyle z}
{
σ
/
2
,
σ
i
/
2
,
−
σ
/
2
,
−
σ
i
/
2
}
{\displaystyle \{\sigma /2,\sigma i/2,-\sigma /2,-\sigma i/2\}}
The complete integral has the value:
∫
0
∞
d
t
t
4
+
1
=
1
4
B
(
1
4
,
1
4
)
=
σ
2
=
1.85407
46773
01371
…
{\displaystyle \int _{0}^{\infty }{\frac {\mathrm {d} t}{\sqrt {t^{4}+1}}}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{4}}{\bigr )}={\frac {\sigma }{2}}=1.85407\;46773\;01371\ldots }
Therefore, the two defined functions have following relation to each other:
slh
z
=
clh
(
σ
2
−
z
)
{\displaystyle \operatorname {slh} z={\operatorname {clh} }{{\Bigl (}{\frac {\sigma }{2}}-z{\Bigr )}}}
The product of hyperbolic lemniscate sine and hyperbolic lemniscate cosine is equal to one:
slh
z
clh
z
=
1
{\displaystyle \operatorname {slh} z\,\operatorname {clh} z=1}
The functions
slh
{\displaystyle \operatorname {slh} }
clh
{\displaystyle \operatorname {clh} }
{
σ
,
σ
i
}
{\displaystyle \{\sigma ,\sigma i\}}
The hyperbolic lemniscate functions can be expressed in terms of lemniscate sine and lemniscate cosine:
slh
(
2
z
)
=
(
1
+
cl
2
z
)
sl
z
2
cl
z
{\displaystyle \operatorname {slh} {\bigl (}{\sqrt {2}}z{\bigr )}={\frac {(1+\operatorname {cl} ^{2}z)\operatorname {sl} z}{{\sqrt {2}}\operatorname {cl} z}}}
clh
(
2
z
)
=
(
1
+
sl
2
z
)
cl
z
2
sl
z
{\displaystyle \operatorname {clh} {\bigl (}{\sqrt {2}}z{\bigr )}={\frac {(1+\operatorname {sl} ^{2}z)\operatorname {cl} z}{{\sqrt {2}}\operatorname {sl} z}}}
But there is also a relation to the Jacobi elliptic functions with the elliptic modulus one by square root of two:
slh
z
=
sn
(
z
;
1
/
2
)
cd
(
z
;
1
/
2
)
{\displaystyle \operatorname {slh} z={\frac {\operatorname {sn} (z;1/{\sqrt {2}})}{\operatorname {cd} (z;1/{\sqrt {2}})}}}
clh
z
=
cd
(
z
;
1
/
2
)
sn
(
z
;
1
/
2
)
{\displaystyle \operatorname {clh} z={\frac {\operatorname {cd} (z;1/{\sqrt {2}})}{\operatorname {sn} (z;1/{\sqrt {2}})}}}
The hyperbolic lemniscate sine has following imaginary relation to the lemniscate sine:
slh
z
=
1
−
i
2
sl
(
1
+
i
2
z
)
=
sl
(
−
1
4
z
)
−
1
4
{\displaystyle \operatorname {slh} z={\frac {1-i}{\sqrt {2}}}\operatorname {sl} \left({\frac {1+i}{\sqrt {2}}}z\right)={\frac {\operatorname {sl} \left({\sqrt[{4}]{-1}}z\right)}{\sqrt[{4}]{-1}}}}
This is analogous to the relationship between hyperbolic and trigonometric sine:
sinh
z
=
−
i
sin
(
i
z
)
=
sin
(
−
1
2
z
)
−
1
2
{\displaystyle \sinh z=-i\sin(iz)={\frac {\sin \left({\sqrt[{2}]{-1}}z\right)}{\sqrt[{2}]{-1}}}}
Relation to quartic Fermat curve
Hyperbolic Lemniscate Tangent and Cotangent
This image shows the standardized superelliptic Fermat squircle curve of the fourth degree:
Superellipse with the relation
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
In a quartic Fermat curve
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
squircle ) the hyperbolic lemniscate sine and cosine are analogous to the tangent and cotangent functions in a unit circle
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1}
L
{\displaystyle L}
, the hyperbolic lemniscate sine of twice the enclosed area between this line and the x-axis is the y-coordinate of the intersection of
L
{\displaystyle L}
with the line
x
=
1
{\displaystyle x=1}
[ 74]
π
{\displaystyle \pi }
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1}
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
σ
{\displaystyle \sigma }
M
(
1
,
1
/
2
)
=
π
σ
{\displaystyle M(1,1/{\sqrt {2}})={\frac {\pi }{\sigma }}}
where
M
{\displaystyle M}
arithmetic–geometric mean .
The hyperbolic lemniscate sine satisfies the argument addition identity:
slh
(
a
+
b
)
=
slh
a
slh
′
b
+
slh
b
slh
′
a
1
−
slh
2
a
slh
2
b
{\displaystyle \operatorname {slh} (a+b)={\frac {\operatorname {slh} a\operatorname {slh} 'b+\operatorname {slh} b\operatorname {slh} 'a}{1-\operatorname {slh} ^{2}a\,\operatorname {slh} ^{2}b}}}
When
u
{\displaystyle u}
antiderivative of
slh
{\displaystyle \operatorname {slh} }
clh
{\displaystyle \operatorname {clh} }
d
d
u
slh
(
u
)
=
1
+
slh
(
u
)
4
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} u}}\operatorname {slh} (u)={\sqrt {1+\operatorname {slh} (u)^{4}}}}
d
d
u
clh
(
u
)
=
−
1
+
clh
(
u
)
4
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} u}}\operatorname {clh} (u)=-{\sqrt {1+\operatorname {clh} (u)^{4}}}}
d
d
u
1
2
arsinh
[
slh
(
u
)
2
]
=
slh
(
u
)
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} u}}\,{\frac {1}{2}}\operatorname {arsinh} {\bigl [}\operatorname {slh} (u)^{2}{\bigr ]}=\operatorname {slh} (u)}
d
d
u
−
1
2
arsinh
[
clh
(
u
)
2
]
=
clh
(
u
)
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} u}}-\,{\frac {1}{2}}\operatorname {arsinh} {\bigl [}\operatorname {clh} (u)^{2}{\bigr ]}=\operatorname {clh} (u)}
There are also the Hyperbolic lemniscate tangent and the Hyperbolic lemniscate coangent als further functions:
The functions tlh and ctlh fulfill the identities described in the differential equation mentioned:
tlh
(
2
u
)
=
sin
4
(
2
u
)
=
sl
(
u
)
cl
2
u
+
1
sl
2
u
+
cl
2
u
{\displaystyle {\text{tlh}}({\sqrt {2}}\,u)=\sin _{4}({\sqrt {2}}\,u)=\operatorname {sl} (u){\sqrt {\frac {\operatorname {cl} ^{2}u+1}{\operatorname {sl} ^{2}u+\operatorname {cl} ^{2}u}}}}
ctlh
(
2
u
)
=
cos
4
(
2
u
)
=
cl
(
u
)
sl
2
u
+
1
sl
2
u
+
cl
2
u
{\displaystyle {\text{ctlh}}({\sqrt {2}}\,u)=\cos _{4}({\sqrt {2}}\,u)=\operatorname {cl} (u){\sqrt {\frac {\operatorname {sl} ^{2}u+1}{\operatorname {sl} ^{2}u+\operatorname {cl} ^{2}u}}}}
The functional designation sl stands for the lemniscatic sine and the designation cl stands for the lemniscatic cosine.
In addition, those relations to the Jacobi elliptic functions are valid:
tlh
(
u
)
=
sn
(
u
;
1
2
2
)
cd
(
u
;
1
2
2
)
4
+
sn
(
u
;
1
2
2
)
4
4
{\displaystyle {\text{tlh}}(u)={\frac {{\text{sn}}(u;{\tfrac {1}{2}}{\sqrt {2}})}{\sqrt[{4}]{{\text{cd}}(u;{\tfrac {1}{2}}{\sqrt {2}})^{4}+{\text{sn}}(u;{\tfrac {1}{2}}{\sqrt {2}})^{4}}}}}
ctlh
(
u
)
=
cd
(
u
;
1
2
2
)
cd
(
u
;
1
2
2
)
4
+
sn
(
u
;
1
2
2
)
4
4
{\displaystyle {\text{ctlh}}(u)={\frac {{\text{cd}}(u;{\tfrac {1}{2}}{\sqrt {2}})}{\sqrt[{4}]{{\text{cd}}(u;{\tfrac {1}{2}}{\sqrt {2}})^{4}+{\text{sn}}(u;{\tfrac {1}{2}}{\sqrt {2}})^{4}}}}}
When
u
{\displaystyle u}
quarter period integral of
tlh
{\displaystyle \operatorname {tlh} }
ctlh
{\displaystyle \operatorname {ctlh} }
d
d
u
tlh
(
u
)
=
ctlh
(
u
)
3
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} u}}\operatorname {tlh} (u)=\operatorname {ctlh} (u)^{3}}
d
d
u
ctlh
(
u
)
=
−
tlh
(
u
)
3
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} u}}\operatorname {ctlh} (u)=-\operatorname {tlh} (u)^{3}}
∫
0
ϖ
/
2
tlh
(
u
)
d
u
=
ϖ
2
{\displaystyle \int _{0}^{\varpi /{\sqrt {2}}}\operatorname {tlh} (u)\,\mathrm {d} u={\frac {\varpi }{2}}}
∫
0
ϖ
/
2
ctlh
(
u
)
d
u
=
ϖ
2
{\displaystyle \int _{0}^{\varpi /{\sqrt {2}}}\operatorname {ctlh} (u)\,\mathrm {d} u={\frac {\varpi }{2}}}
Derivation of the Hyperbolic Lemniscate functions
With respect to the quartic Fermat curve
x
4
+
y
4
=
1
{\displaystyle x^{4}+y^{4}=1}
slh
{\displaystyle \operatorname {slh} }
clh
{\displaystyle \operatorname {clh} }
sin
4
{\displaystyle \sin _{4}}
cos
4
{\displaystyle \cos _{4}}
[ 75] The horizontal and vertical coordinates of this superellipse are dependent on twice the enclosed area w = 2A, so the following conditions must be met:
x
(
w
)
4
+
y
(
w
)
4
=
1
{\displaystyle x(w)^{4}+y(w)^{4}=1}
d
d
w
x
(
w
)
=
−
y
(
w
)
3
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} w}}x(w)=-y(w)^{3}}
d
d
w
y
(
w
)
=
x
(
w
)
3
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} w}}y(w)=x(w)^{3}}
x
(
w
=
0
)
=
1
{\displaystyle x(w=0)=1}
y
(
w
=
0
)
=
0
{\displaystyle y(w=0)=0}
The solutions to this system of equations are as follows:
x
(
w
)
=
cl
(
1
2
2
w
)
[
sl
(
1
2
2
w
)
2
+
1
]
1
/
2
[
sl
(
1
2
2
w
)
2
+
cl
(
1
2
2
w
)
2
]
−
1
/
2
{\displaystyle x(w)=\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}]^{-1/2}}
y
(
w
)
=
sl
(
1
2
2
w
)
[
cl
(
1
2
2
w
)
2
+
1
]
1
/
2
[
sl
(
1
2
2
w
)
2
+
cl
(
1
2
2
w
)
2
]
−
1
/
2
{\displaystyle y(w)=\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}]^{-1/2}}
The following therefore applies to the quotient:
y
(
w
)
x
(
w
)
=
sl
(
1
2
2
w
)
[
cl
(
1
2
2
w
)
2
+
1
]
1
/
2
cl
(
1
2
2
w
)
[
sl
(
1
2
2
w
)
2
+
1
]
1
/
2
=
slh
(
w
)
{\displaystyle {\frac {y(w)}{x(w)}}={\frac {\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}}{\operatorname {cl} ({\tfrac {1}{2}}{\sqrt {2}}w)[\operatorname {sl} ({\tfrac {1}{2}}{\sqrt {2}}w)^{2}+1]^{1/2}}}=\operatorname {slh} (w)}
The functions x(w) and y(w) are called cotangent hyperbolic lemniscatus and hyperbolic tangent .
x
(
w
)
=
ctlh
(
w
)
{\displaystyle x(w)={\text{ctlh}}(w)}
y
(
w
)
=
tlh
(
w
)
{\displaystyle y(w)={\text{tlh}}(w)}
The sketch also shows the fact that the derivation of the Areasinus hyperbolic lemniscatus function is equal to the reciprocal of the square root of the successor of the fourth power function.
First proof: comparison with the derivative of the arctangent
There is a black diagonal on the sketch shown on the right. The length of the segment that runs perpendicularly from the intersection of this black diagonal with the red vertical axis to the point (1|0) should be called s. And the length of the section of the black diagonal from the coordinate origin point to the point of intersection of this diagonal with the cyan curved line of the superellipse has the following value depending on the slh value:
D
(
s
)
=
(
1
s
4
+
1
4
)
2
+
(
s
s
4
+
1
4
)
2
=
s
2
+
1
s
4
+
1
4
{\displaystyle D(s)={\sqrt {{\biggl (}{\frac {1}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}+{\biggl (}{\frac {s}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}}}={\frac {\sqrt {s^{2}+1}}{\sqrt[{4}]{s^{4}+1}}}}
This connection is described by the Pythagorean theorem .
An analogous unit circle results in the arctangent of the circle trigonometric with the described area allocation.
The following derivation applies to this:
d
d
s
arctan
(
s
)
=
1
s
2
+
1
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} s}}\arctan(s)={\frac {1}{s^{2}+1}}}
To determine the derivation of the areasinus lemniscatus hyperbolicus, the comparison of the infinitesimally small triangular areas for the same diagonal in the superellipse and the unit circle is set up below. Because the summation of the infinitesimally small triangular areas describes the area dimensions. In the case of the superellipse in the picture, half of the area concerned is shown in green. Because of the quadratic ratio of the areas to the lengths of triangles with the same infinitesimally small angle at the origin of the coordinates, the following formula applies:
d
d
s
aslh
(
s
)
=
[
d
d
s
arctan
(
s
)
]
D
(
s
)
2
=
1
s
2
+
1
D
(
s
)
2
=
1
s
2
+
1
(
s
2
+
1
s
4
+
1
4
)
2
=
1
s
4
+
1
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} s}}{\text{aslh}}(s)={\biggl [}{\frac {\mathrm {d} }{\mathrm {d} s}}\arctan(s){\biggr ]}D(s)^{2}={\frac {1}{s^{2}+1}}D(s)^{2}={\frac {1}{s^{2}+1}}{\biggl (}{\frac {\sqrt {s^{2}+1}}{\sqrt[{4}]{s^{4}+1}}}{\biggr )}^{2}={\frac {1}{\sqrt {s^{4}+1}}}}
In the picture shown, the area tangent lemniscatus hyperbolicus assigns the height of the intersection of the diagonal and the curved line to twice the green area. The green area itself is created as the difference integral of the superellipse function from zero to the relevant height value minus the area of the adjacent triangle:
atlh
(
v
)
=
2
(
∫
0
v
1
−
w
4
4
d
w
)
−
v
1
−
v
4
4
{\displaystyle {\text{atlh}}(v)=2{\biggl (}\int _{0}^{v}{\sqrt[{4}]{1-w^{4}}}\mathrm {d} w{\biggr )}-v{\sqrt[{4}]{1-v^{4}}}}
d
d
v
atlh
(
v
)
=
2
1
−
v
4
4
−
(
d
d
v
v
1
−
v
4
4
)
=
1
(
1
−
v
4
)
3
/
4
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} v}}{\text{atlh}}(v)=2{\sqrt[{4}]{1-v^{4}}}-{\biggl (}{\frac {\mathrm {d} }{\mathrm {d} v}}v{\sqrt[{4}]{1-v^{4}}}{\biggr )}={\frac {1}{(1-v^{4})^{3/4}}}}
The following transformation applies:
aslh
(
x
)
=
atlh
(
x
x
4
+
1
4
)
{\displaystyle {\text{aslh}}(x)={\text{atlh}}{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}}
And so, according to the chain rule , this derivation holds:
d
d
x
aslh
(
x
)
=
d
d
x
atlh
(
x
x
4
+
1
4
)
=
(
d
d
x
x
x
4
+
1
4
)
[
1
−
(
x
x
4
+
1
4
)
4
]
−
3
/
4
=
{\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}{\text{aslh}}(x)={\frac {\mathrm {d} }{\mathrm {d} x}}{\text{atlh}}{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}={\biggl (}{\frac {\mathrm {d} }{\mathrm {d} x}}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}{\biggl [}1-{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}^{4}{\biggr ]}^{-3/4}=}
=
1
(
x
4
+
1
)
5
/
4
[
1
−
(
x
x
4
+
1
4
)
4
]
−
3
/
4
=
1
(
x
4
+
1
)
5
/
4
(
1
x
4
+
1
)
−
3
/
4
=
1
x
4
+
1
{\displaystyle ={\frac {1}{(x^{4}+1)^{5/4}}}{\biggl [}1-{\biggl (}{\frac {x}{\sqrt[{4}]{x^{4}+1}}}{\biggr )}^{4}{\biggr ]}^{-3/4}={\frac {1}{(x^{4}+1)^{5/4}}}{\biggl (}{\frac {1}{x^{4}+1}}{\biggr )}^{-3/4}={\frac {1}{\sqrt {x^{4}+1}}}}
Specific values
This list shows the values of the Hyperbolic Lemniscate Sine accurately. Recall that,
∫
0
∞
d
t
t
4
+
1
=
1
4
B
(
1
4
,
1
4
)
=
ϖ
2
=
σ
2
=
1.85407
…
{\displaystyle \int _{0}^{\infty }{\frac {\operatorname {d} t}{\sqrt {t^{4}+1}}}={\tfrac {1}{4}}\mathrm {B} {\bigl (}{\tfrac {1}{4}},{\tfrac {1}{4}}{\bigr )}={\frac {\varpi }{\sqrt {2}}}={\frac {\sigma }{2}}=1.85407\ldots }
whereas
1
2
B
(
1
2
,
1
2
)
=
π
2
,
{\displaystyle {\tfrac {1}{2}}\mathrm {B} {\bigl (}{\tfrac {1}{2}},{\tfrac {1}{2}}{\bigr )}={\tfrac {\pi }{2}},}
slh
(
ϖ
2
2
)
=
slh
(
σ
4
)
=
1
{\displaystyle {\operatorname {slh} }{\bigl (}{\tfrac {\varpi }{2{\sqrt {2}}}}{\bigr )}={\operatorname {slh} }{\bigl (}{\tfrac {\sigma }{4}}{\bigr )}=1}
sin
(
π
2
)
=
1
{\displaystyle {\sin }{\bigl (}{\tfrac {\pi }{2}}{\bigr )}=1}
slh
(
ϖ
2
2
)
=
1
{\displaystyle \operatorname {slh} \,\left({\frac {\varpi }{2{\sqrt {2}}}}\right)=1}
slh
(
ϖ
3
2
)
=
1
3
4
2
3
−
3
4
{\displaystyle \operatorname {slh} \,\left({\frac {\varpi }{3{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{3}}}{\sqrt[{4}]{2{\sqrt {3}}-3}}}
slh
(
2
ϖ
3
2
)
=
2
3
+
3
4
{\displaystyle \operatorname {slh} \,\left({\frac {2\varpi }{3{\sqrt {2}}}}\right)={\sqrt[{4}]{2{\sqrt {3}}+3}}}
slh
(
ϖ
4
2
)
=
1
2
4
(
2
+
1
−
1
)
{\displaystyle \operatorname {slh} \,\left({\frac {\varpi }{4{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{2}}}({\sqrt {{\sqrt {2}}+1}}-1)}
slh
(
3
ϖ
4
2
)
=
1
2
4
(
2
+
1
+
1
)
{\displaystyle \operatorname {slh} \,\left({\frac {3\varpi }{4{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{2}}}({\sqrt {{\sqrt {2}}+1}}+1)}
slh
(
ϖ
5
2
)
=
1
8
4
5
−
1
20
4
−
5
+
1
=
2
5
−
2
4
sin
(
1
20
π
)
sin
(
3
20
π
)
{\displaystyle \operatorname {slh} \,\left({\frac {\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{8}}}{\sqrt {{\sqrt {5}}-1}}{\sqrt {{\sqrt[{4}]{20}}-{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {\sin({\tfrac {1}{20}}\pi )\sin({\tfrac {3}{20}}\pi )}}}
slh
(
2
ϖ
5
2
)
=
1
2
2
4
(
5
+
1
)
20
4
−
5
+
1
=
2
5
+
2
4
sin
(
1
20
π
)
sin
(
3
20
π
)
{\displaystyle \operatorname {slh} \,\left({\frac {2\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{2{\sqrt[{4}]{2}}}}({\sqrt {5}}+1){\sqrt {{\sqrt[{4}]{20}}-{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}+2}}{\sqrt {\sin({\tfrac {1}{20}}\pi )\sin({\tfrac {3}{20}}\pi )}}}
slh
(
3
ϖ
5
2
)
=
1
8
4
5
−
1
20
4
+
5
+
1
=
2
5
−
2
4
cos
(
1
20
π
)
cos
(
3
20
π
)
{\displaystyle \operatorname {slh} \,\left({\frac {3\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{\sqrt[{4}]{8}}}{\sqrt {{\sqrt {5}}-1}}{\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}-2}}{\sqrt {\cos({\tfrac {1}{20}}\pi )\cos({\tfrac {3}{20}}\pi )}}}
slh
(
4
ϖ
5
2
)
=
1
2
2
4
(
5
+
1
)
20
4
+
5
+
1
=
2
5
+
2
4
cos
(
1
20
π
)
cos
(
3
20
π
)
{\displaystyle \operatorname {slh} \,\left({\frac {4\varpi }{5{\sqrt {2}}}}\right)={\frac {1}{2{\sqrt[{4}]{2}}}}({\sqrt {5}}+1){\sqrt {{\sqrt[{4}]{20}}+{\sqrt {{\sqrt {5}}+1}}}}=2{\sqrt[{4}]{{\sqrt {5}}+2}}{\sqrt {\cos({\tfrac {1}{20}}\pi )\cos({\tfrac {3}{20}}\pi )}}}
slh
(
ϖ
6
2
)
=
1
2
(
2
3
+
3
+
1
)
(
1
−
2
3
−
3
4
)
{\displaystyle \operatorname {slh} \,\left({\frac {\varpi }{6{\sqrt {2}}}}\right)={\frac {1}{2}}({\sqrt {2{\sqrt {3}}+3}}+1)(1-{\sqrt[{4}]{2{\sqrt {3}}-3}})}
slh
(
5
ϖ
6
2
)
=
1
2
(
2
3
+
3
+
1
)
(
1
+
2
3
−
3
4
)
{\displaystyle \operatorname {slh} \,\left({\frac {5\varpi }{6{\sqrt {2}}}}\right)={\frac {1}{2}}({\sqrt {2{\sqrt {3}}+3}}+1)(1+{\sqrt[{4}]{2{\sqrt {3}}-3}})}
That table shows the most important values of the Hyperbolic Lemniscate Tangent and Cotangent functions:
z
{\displaystyle z}
clh
z
{\displaystyle \operatorname {clh} z}
slh
z
{\displaystyle \operatorname {slh} z}
ctlh
z
=
cos
4
z
{\displaystyle \operatorname {ctlh} z=\cos _{4}z}
tlh
z
=
sin
4
z
{\displaystyle \operatorname {tlh} z=\sin _{4}z}
0
{\displaystyle 0}
∞
{\displaystyle \infty }
0
{\displaystyle 0}
1
{\displaystyle 1}
0
{\displaystyle 0}
1
4
σ
{\displaystyle {\tfrac {1}{4}}\sigma }
1
{\displaystyle 1}
1
{\displaystyle 1}
1
/
2
4
{\displaystyle 1{\big /}{\sqrt[{4}]{2}}}
1
/
2
4
{\displaystyle 1{\big /}{\sqrt[{4}]{2}}}
1
2
σ
{\displaystyle {\tfrac {1}{2}}\sigma }
0
{\displaystyle 0}
∞
{\displaystyle \infty }
0
{\displaystyle 0}
1
{\displaystyle 1}
3
4
σ
{\displaystyle {\tfrac {3}{4}}\sigma }
−
1
{\displaystyle -1}
−
1
{\displaystyle -1}
−
1
/
2
4
{\displaystyle -1{\big /}{\sqrt[{4}]{2}}}
1
/
2
4
{\displaystyle 1{\big /}{\sqrt[{4}]{2}}}
σ
{\displaystyle \sigma }
∞
{\displaystyle \infty }
0
{\displaystyle 0}
−
1
{\displaystyle -1}
0
{\displaystyle 0}
Combination and halving theorems
Given the hyperbolic lemniscate tangent (
tlh
{\displaystyle \operatorname {tlh} }
hyperbolic lemniscate cotangent (
ctlh
{\displaystyle \operatorname {ctlh} }
hyperbolic lemniscate area functions from the section on inverse functions,
aslh
(
x
)
=
∫
0
x
1
y
4
+
1
d
y
{\displaystyle \operatorname {aslh} (x)=\int _{0}^{x}{\frac {1}{\sqrt {y^{4}+1}}}\mathrm {d} y}
aclh
(
x
)
=
∫
x
∞
1
y
4
+
1
d
y
{\displaystyle \operatorname {aclh} (x)=\int _{x}^{\infty }{\frac {1}{\sqrt {y^{4}+1}}}\mathrm {d} y}
Then the following identities can be established,
tlh
[
aslh
(
x
)
]
=
ctlh
[
aclh
(
x
)
]
=
x
x
4
+
1
4
{\displaystyle {\text{tlh}}{\bigl [}{\text{aslh}}(x){\bigr ]}={\text{ctlh}}{\bigl [}{\text{aclh}}(x){\bigr ]}={\frac {x}{\sqrt[{4}]{x^{4}+1}}}}
ctlh
[
aslh
(
x
)
]
=
tlh
[
aclh
(
x
)
]
=
1
x
4
+
1
4
{\displaystyle {\text{ctlh}}{\bigl [}{\text{aslh}}(x){\bigr ]}={\text{tlh}}{\bigl [}{\text{aclh}}(x){\bigr ]}={\frac {1}{\sqrt[{4}]{x^{4}+1}}}}
hence the 4th power of
tlh
{\displaystyle \operatorname {tlh} }
ctlh
{\displaystyle \operatorname {ctlh} }
tlh
[
aslh
(
x
)
]
4
+
ctlh
[
aslh
(
x
)
]
4
=
1
{\displaystyle {\text{tlh}}{\bigl [}{\text{aslh}}(x){\bigr ]}^{4}+{\text{ctlh}}{\bigl [}{\text{aslh}}(x){\bigr ]}^{4}=1}
tlh
[
aclh
(
x
)
]
4
+
ctlh
[
aclh
(
x
)
]
4
=
1
{\displaystyle {\text{tlh}}{\bigl [}{\text{aclh}}(x){\bigr ]}^{4}+{\text{ctlh}}{\bigl [}{\text{aclh}}(x){\bigr ]}^{4}=1}
so a 4th power version of the Pythagorean theorem . The bisection theorem of the hyperbolic sinus lemniscatus reads as follows:
slh
[
1
2
aslh
(
x
)
]
=
2
x
x
2
+
1
+
x
4
+
1
+
x
4
+
1
−
x
2
+
1
{\displaystyle {\text{slh}}{\bigl [}{\tfrac {1}{2}}{\text{aslh}}(x){\bigr ]}={\frac {{\sqrt {2}}x}{{\sqrt {x^{2}+1+{\sqrt {x^{4}+1}}}}+{\sqrt {{\sqrt {x^{4}+1}}-x^{2}+1}}}}}
This formula can be revealed as a combination of the following two formulas:
a
s
l
h
(
x
)
=
2
arcsl
[
x
(
x
4
+
1
+
1
)
−
1
/
2
]
{\displaystyle \mathrm {aslh} (x)={\sqrt {2}}\,{\text{arcsl}}{\bigl [}x({\sqrt {x^{4}+1}}+1)^{-1/2}{\bigr ]}}
arcsl
(
x
)
=
2
aslh
(
2
x
1
+
x
2
+
1
−
x
2
)
{\displaystyle {\text{arcsl}}(x)={\sqrt {2}}\,{\text{aslh}}{\bigl (}{\frac {{\sqrt {2}}x}{{\sqrt {1+x^{2}}}+{\sqrt {1-x^{2}}}}}{\bigr )}}
In addition, the following formulas are valid for all real values
x
∈
R
{\displaystyle x\in \mathbb {R} }
slh
[
1
2
aclh
(
x
)
]
=
x
4
+
1
+
x
2
−
2
x
x
4
+
1
+
x
2
=
(
x
4
+
1
−
x
2
+
1
)
−
1
/
2
(
x
4
+
1
+
1
−
x
)
{\displaystyle {\text{slh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}(x){\bigr ]}={\sqrt {{\sqrt {x^{4}+1}}+x^{2}-{\sqrt {2}}x{\sqrt {{\sqrt {x^{4}+1}}+x^{2}}}}}={\bigl (}{\sqrt {x^{4}+1}}-x^{2}+1{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}-x{\bigr )}}
clh
[
1
2
aclh
(
x
)
]
=
x
4
+
1
+
x
2
+
2
x
x
4
+
1
+
x
2
=
(
x
4
+
1
−
x
2
+
1
)
−
1
/
2
(
x
4
+
1
+
1
+
x
)
{\displaystyle {\text{clh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}(x){\bigr ]}={\sqrt {{\sqrt {x^{4}+1}}+x^{2}+{\sqrt {2}}x{\sqrt {{\sqrt {x^{4}+1}}+x^{2}}}}}={\bigl (}{\sqrt {x^{4}+1}}-x^{2}+1{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}+x{\bigr )}}
These identities follow from the last-mentioned formula:
tlh
[
1
2
aclh
(
x
)
]
2
=
1
2
2
−
2
2
x
x
4
+
1
−
x
2
=
(
2
x
2
+
2
+
2
x
4
+
1
)
−
1
/
2
(
x
4
+
1
+
1
−
x
)
{\displaystyle {\text{tlh}}[{\tfrac {1}{2}}{\text{aclh}}(x)]^{2}={\tfrac {1}{2}}{\sqrt {2-2{\sqrt {2}}\,x{\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}}={\bigl (}2x^{2}+2+2{\sqrt {x^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}-x{\bigr )}}
ctlh
[
1
2
aclh
(
x
)
]
2
=
1
2
2
+
2
2
x
x
4
+
1
−
x
2
=
(
2
x
2
+
2
+
2
x
4
+
1
)
−
1
/
2
(
x
4
+
1
+
1
+
x
)
{\displaystyle {\text{ctlh}}[{\tfrac {1}{2}}{\text{aclh}}(x)]^{2}={\tfrac {1}{2}}{\sqrt {2+2{\sqrt {2}}\,x{\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}}={\bigl (}2x^{2}+2+2{\sqrt {x^{4}+1}}{\bigr )}^{-1/2}{\bigl (}{\sqrt {{\sqrt {x^{4}+1}}+1}}+x{\bigr )}}
Hence, their 4th powers again equal one,
tlh
[
1
2
aclh
(
x
)
]
4
+
ctlh
[
1
2
aclh
(
x
)
]
4
=
1
{\displaystyle {\text{tlh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}(x){\bigr ]}^{4}+{\text{ctlh}}{\bigl [}{\tfrac {1}{2}}{\text{aclh}}(x){\bigr ]}^{4}=1}
The following formulas for the lemniscatic sine and lemniscatic cosine are closely related:
sl
[
1
2
2
aclh
(
x
)
]
=
cl
[
1
2
2
aslh
(
x
)
]
=
x
4
+
1
−
x
2
{\displaystyle {\text{sl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aclh}}(x)]={\text{cl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aslh}}(x)]={\sqrt {{\sqrt {x^{4}+1}}-x^{2}}}}
sl
[
1
2
2
aslh
(
x
)
]
=
cl
[
1
2
2
aclh
(
x
)
]
=
x
(
x
4
+
1
+
1
)
−
1
/
2
{\displaystyle {\text{sl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aslh}}(x)]={\text{cl}}[{\tfrac {1}{2}}{\sqrt {2}}\,{\text{aclh}}(x)]=x{\bigl (}{\sqrt {x^{4}+1}}+1{\bigr )}^{-1/2}}
Analogous to the determination of the improper integral in the Gaussian bell curve function , the coordinate transformation of a general cylinder can be used to calculate the integral from 0 to the positive infinity in the function
f
(
x
)
=
exp
(
−
x
4
)
{\displaystyle f(x)=\exp(-x^{4})}
This is the cylindrical coordinate transformation in the Gaussian bell curve function:
[
∫
0
∞
exp
(
−
x
2
)
d
x
]
2
=
∫
0
∞
∫
0
∞
exp
(
−
y
2
−
z
2
)
d
y
d
z
=
{\displaystyle {\biggl [}\int _{0}^{\infty }\exp(-x^{2})\,\mathrm {d} x{\biggr ]}^{2}=\int _{0}^{\infty }\int _{0}^{\infty }\exp(-y^{2}-z^{2})\,\mathrm {d} y\,\mathrm {d} z=}
=
∫
0
π
/
2
∫
0
∞
det
[
∂
/
∂
r
r
cos
(
ϕ
)
∂
/
∂
ϕ
r
cos
(
ϕ
)
∂
/
∂
r
r
sin
(
ϕ
)
∂
/
∂
ϕ
r
sin
(
ϕ
)
]
exp
{
−
[
r
cos
(
ϕ
)
]
2
−
[
r
sin
(
ϕ
)
]
2
}
d
r
d
ϕ
=
{\displaystyle =\int _{0}^{\pi /2}\int _{0}^{\infty }\det {\begin{bmatrix}\partial /\partial r\,\,r\cos(\phi )&\partial /\partial \phi \,\,r\cos(\phi )\\\partial /\partial r\,\,r\sin(\phi )&\partial /\partial \phi \,\,r\sin(\phi )\end{bmatrix}}\exp {\bigl \{}-{\bigl [}r\cos(\phi ){\bigr ]}^{2}-{\bigl [}r\sin(\phi ){\bigr ]}^{2}{\bigr \}}\,\mathrm {d} r\,\mathrm {d} \phi =}
=
∫
0
π
/
2
∫
0
∞
r
exp
(
−
r
2
)
d
r
d
ϕ
=
∫
0
π
/
2
1
2
d
ϕ
=
π
4
{\displaystyle =\int _{0}^{\pi /2}\int _{0}^{\infty }r\exp(-r^{2})\,\mathrm {d} r\,\mathrm {d} \phi =\int _{0}^{\pi /2}{\frac {1}{2}}\,\mathrm {d} \phi ={\frac {\pi }{4}}}
And this is the analogous coordinate transformation for the lemniscatory case:
[
∫
0
∞
exp
(
−
x
4
)
d
x
]
2
=
∫
0
∞
∫
0
∞
exp
(
−
y
4
−
z
4
)
d
y
d
z
=
{\displaystyle {\biggl [}\int _{0}^{\infty }\exp(-x^{4})\,\mathrm {d} x{\biggr ]}^{2}=\int _{0}^{\infty }\int _{0}^{\infty }\exp(-y^{4}-z^{4})\,\mathrm {d} y\,\mathrm {d} z=}
=
∫
0
ϖ
/
2
∫
0
∞
det
[
∂
/
∂
r
r
ctlh
(
ϕ
)
∂
/
∂
ϕ
r
ctlh
(
ϕ
)
∂
/
∂
r
r
tlh
(
ϕ
)
∂
/
∂
ϕ
r
tlh
(
ϕ
)
]
exp
{
−
[
r
ctlh
(
ϕ
)
]
4
−
[
r
tlh
(
ϕ
)
]
4
}
d
r
d
ϕ
=
{\displaystyle =\int _{0}^{\varpi /{\sqrt {2}}}\int _{0}^{\infty }\det {\begin{bmatrix}\partial /\partial r\,\,r\,{\text{ctlh}}(\phi )&\partial /\partial \phi \,\,r\,{\text{ctlh}}(\phi )\\\partial /\partial r\,\,r\,{\text{tlh}}(\phi )&\partial /\partial \phi \,\,r\,{\text{tlh}}(\phi )\end{bmatrix}}\exp {\bigl \{}-{\bigl [}r\,{\text{ctlh}}(\phi ){\bigr ]}^{4}-{\bigl [}r\,{\text{tlh}}(\phi ){\bigr ]}^{4}{\bigr \}}\,\mathrm {d} r\,\mathrm {d} \phi =}
=
∫
0
ϖ
/
2
∫
0
∞
r
exp
(
−
r
4
)
d
r
d
ϕ
=
∫
0
ϖ
/
2
π
4
d
ϕ
=
ϖ
π
4
2
{\displaystyle =\int _{0}^{\varpi /{\sqrt {2}}}\int _{0}^{\infty }r\exp(-r^{4})\,\mathrm {d} r\,\mathrm {d} \phi =\int _{0}^{\varpi /{\sqrt {2}}}{\frac {\sqrt {\pi }}{4}}\,\mathrm {d} \phi ={\frac {\varpi {\sqrt {\pi }}}{4{\sqrt {2}}}}}
In the last line of this elliptically analogous equation chain there is again the original Gauss bell curve integrated with the square function as the inner substitution according to the Chain rule of infinitesimal analytics (analysis).
In both cases, the determinant of the Jacobi matrix is multiplied to the original function in the integration domain.
The resulting new functions in the integration area are then integrated according to the new parameters.
Number theory
In algebraic number theory , every finite abelian extension of the Gaussian rationals
Q
(
i
)
{\displaystyle \mathbb {Q} (i)}
subfield of
Q
(
i
,
ω
n
)
{\displaystyle \mathbb {Q} (i,\omega _{n})}
n
{\displaystyle n}
[ 23] [ 76] Kronecker–Weber theorem for the rational numbers
Q
{\displaystyle \mathbb {Q} }
Q
{\displaystyle \mathbb {Q} }
Q
(
ζ
n
)
{\displaystyle \mathbb {Q} (\zeta _{n})}
n
{\displaystyle n}
Hilbert's twelfth problem .
The field
Q
(
i
,
sl
(
ϖ
/
n
)
)
{\displaystyle \mathbb {Q} (i,\operatorname {sl} (\varpi /n))}
n
{\displaystyle n}
Q
(
i
)
{\displaystyle \mathbb {Q} (i)}
x
{\displaystyle x}
y
{\displaystyle y}
(
1
+
i
)
n
{\displaystyle (1+i)n}
torsion points on the elliptic curve
y
2
=
4
x
3
+
x
{\displaystyle y^{2}=4x^{3}+x}
[ 76]
Hurwitz numbers
The Bernoulli numbers
B
n
{\displaystyle \mathrm {B} _{n}}
B
n
=
lim
z
→
0
d
n
d
z
n
z
e
z
−
1
,
n
≥
0
{\displaystyle \mathrm {B} _{n}=\lim _{z\to 0}{\frac {\mathrm {d} ^{n}}{\mathrm {d} z^{n}}}{\frac {z}{e^{z}-1}},\quad n\geq 0}
and appear in
∑
k
∈
Z
∖
{
0
}
1
k
2
n
=
(
−
1
)
n
−
1
B
2
n
(
2
π
)
2
n
(
2
n
)
!
=
2
ζ
(
2
n
)
,
n
≥
1
{\displaystyle \sum _{k\in \mathbb {Z} \setminus \{0\}}{\frac {1}{k^{2n}}}=(-1)^{n-1}\mathrm {B} _{2n}{\frac {(2\pi )^{2n}}{(2n)!}}=2\zeta (2n),\quad n\geq 1}
where
ζ
{\displaystyle \zeta }
Riemann zeta function .
The Hurwitz numbers
H
n
,
{\displaystyle \mathrm {H} _{n},}
Adolf Hurwitz , are the "lemniscate analogs" of the Bernoulli numbers. They can be defined by[ 77] [ 78]
H
n
=
−
lim
z
→
0
d
n
d
z
n
z
ζ
(
z
;
1
/
4
,
0
)
,
n
≥
0
{\displaystyle \mathrm {H} _{n}=-\lim _{z\to 0}{\frac {\mathrm {d} ^{n}}{\mathrm {d} z^{n}}}z\zeta (z;1/4,0),\quad n\geq 0}
where
ζ
(
⋅
;
1
/
4
,
0
)
{\displaystyle \zeta (\cdot ;1/4,0)}
Weierstrass zeta function with lattice invariants
1
/
4
{\displaystyle 1/4}
0
{\displaystyle 0}
∑
z
∈
Z
[
i
]
∖
{
0
}
1
z
4
n
=
H
4
n
(
2
ϖ
)
4
n
(
4
n
)
!
=
G
4
n
(
i
)
,
n
≥
1
{\displaystyle \sum _{z\in \mathbb {Z} [i]\setminus \{0\}}{\frac {1}{z^{4n}}}=\mathrm {H} _{4n}{\frac {(2\varpi )^{4n}}{(4n)!}}=G_{4n}(i),\quad n\geq 1}
where
Z
[
i
]
{\displaystyle \mathbb {Z} [i]}
Gaussian integers and
G
4
n
{\displaystyle G_{4n}}
Eisenstein series of weight
4
n
{\displaystyle 4n}
∑
n
=
1
∞
n
k
e
2
π
n
−
1
=
{
1
24
−
1
8
π
if
k
=
1
B
k
+
1
2
k
+
2
if
k
≡
1
(
m
o
d
4
)
and
k
≥
5
B
k
+
1
2
k
+
2
+
H
k
+
1
2
k
+
2
(
ϖ
π
)
k
+
1
if
k
≡
3
(
m
o
d
4
)
and
k
≥
3.
{\displaystyle \displaystyle {\begin{array}{ll}\displaystyle \sum _{n=1}^{\infty }{\dfrac {n^{k}}{e^{2\pi n}-1}}={\begin{cases}{\dfrac {1}{24}}-{\dfrac {1}{8\pi }}&{\text{if}}\ k=1\\{\dfrac {\mathrm {B} _{k+1}}{2k+2}}&{\text{if}}\ k\equiv 1\,(\mathrm {mod} \,4)\ {\text{and}}\ k\geq 5\\{\dfrac {\mathrm {B} _{k+1}}{2k+2}}+{\dfrac {\mathrm {H} _{k+1}}{2k+2}}\left({\dfrac {\varpi }{\pi }}\right)^{k+1}&{\text{if}}\ k\equiv 3\,(\mathrm {mod} \,4)\ {\text{and}}\ k\geq 3.\\\end{cases}}\end{array}}}
The Hurwitz numbers can also be determined as follows:
H
4
=
1
/
10
{\displaystyle \mathrm {H} _{4}=1/10}
H
4
n
=
3
(
2
n
−
3
)
(
16
n
2
−
1
)
∑
k
=
1
n
−
1
(
4
n
4
k
)
(
4
k
−
1
)
(
4
(
n
−
k
)
−
1
)
H
4
k
H
4
(
n
−
k
)
,
n
≥
2
{\displaystyle \mathrm {H} _{4n}={\frac {3}{(2n-3)(16n^{2}-1)}}\sum _{k=1}^{n-1}{\binom {4n}{4k}}(4k-1)(4(n-k)-1)\mathrm {H} _{4k}\mathrm {H} _{4(n-k)},\quad n\geq 2}
and
H
n
=
0
{\displaystyle \mathrm {H} _{n}=0}
n
{\displaystyle n}
4
{\displaystyle 4}
[ 79] [ 77]
H
8
=
3
10
,
H
12
=
567
130
,
H
16
=
43
659
170
,
…
{\displaystyle \mathrm {H} _{8}={\frac {3}{10}},\,\mathrm {H} _{12}={\frac {567}{130}},\,\mathrm {H} _{16}={\frac {43\,659}{170}},\,\ldots }
Also[ 80]
denom
H
4
n
=
∏
(
p
−
1
)
|
4
n
p
{\displaystyle \operatorname {denom} \mathrm {H} _{4n}=\prod _{(p-1)|4n}p}
where
p
∈
P
{\displaystyle p\in \mathbb {P} }
p
≢
3
(
mod
4
)
,
{\displaystyle p\not \equiv 3\,({\text{mod}}\,4),}
denom
B
2
n
=
∏
(
p
−
1
)
|
2
n
p
{\displaystyle \operatorname {denom} \mathrm {B} _{2n}=\prod _{(p-1)|2n}p}
where
p
∈
P
{\displaystyle p\in \mathbb {P} }
von Staudt–Clausen theorem ).
In fact, the von Staudt–Clausen theorem determines the fractional part of the Bernoulli numbers:
B
2
n
+
∑
(
p
−
1
)
|
2
n
1
p
∈
Z
,
n
≥
1
{\displaystyle \mathrm {B} _{2n}+\sum _{(p-1)|2n}{\frac {1}{p}}\in \mathbb {Z} ,\quad n\geq 1}
(sequence A000146 OEIS ) where
p
{\displaystyle p}
a
∈
Z
{\displaystyle a\in \mathbb {Z} }
b
∈
Z
{\displaystyle b\in \mathbb {Z} }
p
{\displaystyle p}
p
≡
1
(
m
o
d
4
)
{\displaystyle p\equiv 1\,(\mathrm {mod} \,4)}
p
=
a
2
+
b
2
{\displaystyle p=a^{2}+b^{2}}
Fermat's theorem on sums of two squares ) and
a
≡
b
+
1
(
m
o
d
4
)
{\displaystyle a\equiv b+1\,(\mathrm {mod} \,4)}
p
{\displaystyle p}
2
a
=
ν
(
p
)
{\displaystyle 2a=\nu (p)}
ν
(
p
)
=
p
−
N
p
{\displaystyle \nu (p)=p-{\mathcal {N}}_{p}}
N
p
{\displaystyle {\mathcal {N}}_{p}}
X
3
−
X
≡
Y
2
(
mod
p
)
{\displaystyle X^{3}-X\equiv Y^{2}\,(\operatorname {mod} p)}
X
,
Y
{\displaystyle X,Y}
[ 81] [ 77]
H
4
n
−
1
2
−
∑
(
p
−
1
)
|
4
n
ν
(
p
)
4
n
/
(
p
−
1
)
p
=
def
G
n
∈
Z
,
n
≥
1.
{\displaystyle \mathrm {H} _{4n}-{\frac {1}{2}}-\sum _{(p-1)|4n}{\frac {\nu (p)^{4n/(p-1)}}{p}}\mathrel {\overset {\text{def}}{=}} \mathrm {G} _{n}\in \mathbb {Z} ,\quad n\geq 1.}
The sequence of the integers
G
n
{\displaystyle \mathrm {G} _{n}}
0
,
−
1
,
5
,
253
,
…
.
{\displaystyle 0,-1,5,253,\ldots .}
[ 77]
Let
n
≥
2
{\displaystyle n\geq 2}
4
n
+
1
{\displaystyle 4n+1}
G
n
≡
1
(
m
o
d
4
)
{\displaystyle \mathrm {G} _{n}\equiv 1\,(\mathrm {mod} \,4)}
4
n
+
1
{\displaystyle 4n+1}
G
n
≡
3
(
m
o
d
4
)
{\displaystyle \mathrm {G} _{n}\equiv 3\,(\mathrm {mod} \,4)}
[ 82]
Some authors instead define the Hurwitz numbers as
H
n
′
=
H
4
n
{\displaystyle \mathrm {H} _{n}'=\mathrm {H} _{4n}}
Appearances in Laurent series
The Hurwitz numbers appear in several Laurent series expansions related to the lemniscate functions:[ 83]
sl
2
z
=
∑
n
=
1
∞
2
4
n
(
1
−
(
−
1
)
n
2
2
n
)
H
4
n
4
n
z
4
n
−
2
(
4
n
−
2
)
!
,
|
z
|
<
ϖ
2
sl
′
z
sl
z
=
1
z
−
∑
n
=
1
∞
2
4
n
(
2
−
(
−
1
)
n
2
2
n
)
H
4
n
4
n
z
4
n
−
1
(
4
n
−
1
)
!
,
|
z
|
<
ϖ
2
1
sl
z
=
1
z
−
∑
n
=
1
∞
2
2
n
(
(
−
1
)
n
2
−
2
2
n
)
H
4
n
4
n
z
4
n
−
1
(
4
n
−
1
)
!
,
|
z
|
<
ϖ
1
sl
2
z
=
1
z
2
+
∑
n
=
1
∞
2
4
n
H
4
n
4
n
z
4
n
−
2
(
4
n
−
2
)
!
,
|
z
|
<
ϖ
{\displaystyle {\begin{aligned}\operatorname {sl} ^{2}z&=\sum _{n=1}^{\infty }{\frac {2^{4n}(1-(-1)^{n}2^{2n})\mathrm {H} _{4n}}{4n}}{\frac {z^{4n-2}}{(4n-2)!}},\quad \left|z\right|<{\frac {\varpi }{\sqrt {2}}}\\{\frac {\operatorname {sl} 'z}{\operatorname {sl} {z}}}&={\frac {1}{z}}-\sum _{n=1}^{\infty }{\frac {2^{4n}(2-(-1)^{n}2^{2n})\mathrm {H} _{4n}}{4n}}{\frac {z^{4n-1}}{(4n-1)!}},\quad \left|z\right|<{\frac {\varpi }{\sqrt {2}}}\\{\frac {1}{\operatorname {sl} z}}&={\frac {1}{z}}-\sum _{n=1}^{\infty }{\frac {2^{2n}((-1)^{n}2-2^{2n})\mathrm {H} _{4n}}{4n}}{\frac {z^{4n-1}}{(4n-1)!}},\quad \left|z\right|<\varpi \\{\frac {1}{\operatorname {sl} ^{2}z}}&={\frac {1}{z^{2}}}+\sum _{n=1}^{\infty }{\frac {2^{4n}\mathrm {H} _{4n}}{4n}}{\frac {z^{4n-2}}{(4n-2)!}},\quad \left|z\right|<\varpi \end{aligned}}}
Analogously, in terms of the Bernoulli numbers:
1
sinh
2
z
=
1
z
2
−
∑
n
=
1
∞
2
2
n
B
2
n
2
n
z
2
n
−
2
(
2
n
−
2
)
!
,
|
z
|
<
π
.
{\displaystyle {\frac {1}{\sinh ^{2}z}}={\frac {1}{z^{2}}}-\sum _{n=1}^{\infty }{\frac {2^{2n}\mathrm {B} _{2n}}{2n}}{\frac {z^{2n-2}}{(2n-2)!}},\quad \left|z\right|<\pi .}
A quartic analog of the Legendre symbol
Let
p
{\displaystyle p}
p
≡
1
(
mod
4
)
{\displaystyle p\equiv 1\,({\text{mod}}\,4)}
quartic residue (mod
p
{\displaystyle p}
(
a
p
)
4
{\displaystyle \left({\tfrac {a}{p}}\right)_{4}}
1
{\displaystyle 1}
a
{\displaystyle a}
p
{\displaystyle p}
−
1
{\displaystyle -1}
a
{\displaystyle a}
p
{\displaystyle p}
If
a
{\displaystyle a}
p
{\displaystyle p}
p
′
∈
Z
[
i
]
{\displaystyle p'\in \mathbb {Z} [i]}
[ 84] [ 85]
(
a
p
)
4
=
∏
p
′
sl
(
2
ϖ
a
p
′
/
p
)
sl
(
2
ϖ
p
′
/
p
)
.
{\displaystyle \left({\frac {a}{p}}\right)_{4}=\prod _{p'}{\frac {\operatorname {sl} (2\varpi ap'/p)}{\operatorname {sl} (2\varpi p'/p)}}.}
This theorem is analogous to
(
a
p
)
=
∏
n
=
1
p
−
1
2
sin
(
2
π
a
n
/
p
)
sin
(
2
π
n
/
p
)
{\displaystyle \left({\frac {a}{p}}\right)=\prod _{n=1}^{\frac {p-1}{2}}{\frac {\sin(2\pi an/p)}{\sin(2\pi n/p)}}}
where
(
⋅
⋅
)
{\displaystyle \left({\tfrac {\cdot }{\cdot }}\right)}
Legendre symbol .
World map projections
"The World on a Quincuncial Projection", from Peirce (1879) . The Peirce quincuncial projection , designed by Charles Sanders Peirce of the US Coast Survey in the 1870s, is a world map projection based on the inverse lemniscate sine of stereographically projected points (treated as complex numbers).[ 86]
When lines of constant real or imaginary part are projected onto the complex plane via the hyperbolic lemniscate sine, and thence stereographically projected onto the sphere (see Riemann sphere ), the resulting curves are spherical conics , the spherical analog of planar ellipses and hyperbolas .[ 87] Jacobi elliptic functions ) provide a parametrization for spherical conics.
A conformal map projection from the globe onto the 6 square faces of a cube can also be defined using the lemniscate functions.[ 88] partial differential equations can be effectively solved by conformal mapping, this map from sphere to cube is convenient for atmospheric modeling .[ 89]
See also
Notes
^ Fagnano (1718–1723) ; Euler (1761) ; Gauss (1917) ^ Gauss (1917) p. 199 used the symbols sl and cl for the lemniscate sine and cosine, respectively, and this notation is most common today: see e.g. Cox (1984) p. 316, Eymard & Lafon (2004) p. 204, and Lemmermeyer (2000) p. 240. Ayoub (1984) uses sinlem and coslem . Whittaker & Watson (1920) use the symbols sin lemn and cos lemn . Some sources use the generic letters s c Prasolov & Solovyev (1997) use the letter φ φ′ ^ The circle
x
2
+
y
2
=
x
{\displaystyle x^{2}+y^{2}=x}
(
1
2
,
0
)
{\textstyle {\bigl (}{\tfrac {1}{2}},0{\bigr )}}
r
=
cos
θ
,
{\displaystyle r=\cos \theta ,}
clover under the definition from Cox & Shurman (2005) . This is not the unit-radius circle
x
2
+
y
2
=
1
{\displaystyle x^{2}+y^{2}=1}
(
x
2
+
y
2
)
2
=
x
2
−
y
2
{\displaystyle {\bigl (}x^{2}+y^{2}{\bigr )}{}^{2}=x^{2}-y^{2}}
^ The fundamental periods
(
1
+
i
)
ϖ
{\displaystyle (1+i)\varpi }
(
1
−
i
)
ϖ
{\displaystyle (1-i)\varpi }
^ Robinson (2019a) starts from this definition and thence derives other properties of the lemniscate functions.^ This map was the first ever picture of a Schwarz–Christoffel mapping, in Schwarz (1869) p. 113 .
^ Schappacher (1997) . OEIS sequence A062539 lists the lemniscate constant's decimal digits.^ Levin (2006) ^ Todd (1975) ^ Cox (1984) ^ Dark areas represent zeros, and bright areas represent poles. As the argument of
sl
z
{\displaystyle \operatorname {sl} z}
−
π
{\displaystyle -\pi }
−
π
{\displaystyle -\pi }
π
{\displaystyle \pi }
(
Arg
≈
−
π
/
2
)
{\displaystyle (\operatorname {Arg} \approx -\pi /2)}
(
Arg
≈
0
)
{\displaystyle (\operatorname {Arg} \approx 0)}
(
Arg
≈
π
/
2
)
{\displaystyle (\operatorname {Arg} \approx \pi /2)}
(
Arg
≈
π
)
{\displaystyle (\operatorname {Arg} \approx \pi )}
^ Combining the first and fourth identity gives
sl
z
=
−
i
/
sl
(
z
−
(
1
+
i
)
ϖ
/
2
)
{\displaystyle \operatorname {sl} z=-i/\operatorname {sl} (z-(1+i)\varpi /2)}
Eymard & Lafon (2004) p. 226, without the minus sign at the front of the right-hand side.
^ The even Gaussian integers are the residue class of
0
{\displaystyle 0}
, modulo
1
+
i
{\displaystyle 1+i}
, the black squares on a checkerboard .
^ Prasolov & Solovyev (1997) ; Robinson (2019a) ^ a b Cox (2012) ^ Reinhardt & Walker (2010a) §22.12.6 , §22.12.12 ^ Analogously,
1
sin
z
=
∑
n
∈
Z
(
−
1
)
n
z
+
n
π
.
{\displaystyle {\frac {1}{\sin z}}=\sum _{n\in \mathbb {Z} }{\frac {(-1)^{n}}{z+n\pi }}.}
^ Lindqvist & Peetre (2001) generalizes the first of these forms.^ Ayoub (1984) ; Prasolov & Solovyev (1997) ^ Euler (1761) §44 p. 79 , §47 pp. 80–81^ a b Euler (1761) §46 p. 80 ^ In fact,
i
ε
=
sl
β
ϖ
2
{\displaystyle i^{\varepsilon }=\operatorname {sl} {\tfrac {\beta \varpi }{2}}}
^ a b c Cox & Hyde (2014) ^ Gómez-Molleda & Lario (2019) ^ The fourth root with the least positive principal argument is chosen.
^ The restriction to positive and odd
β
{\displaystyle \beta }
deg
Λ
β
=
|
(
O
/
β
O
)
×
|
{\displaystyle \operatorname {deg} \Lambda _{\beta }=\left|({\mathcal {O}}/\beta {\mathcal {O}})^{\times }\right|}
^ Cox (2013) p. 142, Example 7.29(c)^ Rosen (1981) ^ Eymard & Lafon (2004) p. 200^ And the area enclosed by
L
{\displaystyle {\mathcal {L}}}
1
{\displaystyle 1}
whose enclosed area is a non-constructible number ).
^ Euler (1761) ; Siegel (1969) . Prasolov & Solovyev (1997) use the polar-coordinate representation of the Lemniscate to derive differential arc length, but the result is the same.^ Reinhardt & Walker (2010a) §22.18.E6 ^ Siegel (1969) ; Schappacher (1997) ^ Such numbers are OEIS sequence A003401 .
^ Abel (1827–1828) ; Rosen (1981) ; Prasolov & Solovyev (1997) ^ Euler (1786) ; Sridharan (2004) ; Levien (2008) ^ "A104203" . The On-Line Encyclopedia of Integer Sequences .^ Lomont, J.S.; Brillhart, John (2001). Elliptic Polynomials . CRC Press. pp. 12, 44. ISBN 1-58488-210-7 . ^ a b c d "A193543 - Oeis" .^ Lomont, J.S.; Brillhart, John (2001). Elliptic Polynomials . CRC Press. ISBN 1-58488-210-7 . ^ Lomont, J.S.; Brillhart, John (2001). Elliptic Polynomials . CRC Press. ISBN 1-58488-210-7 . ^ a b "A289695 - Oeis" .^ Wall, H. S. (1948). Analytic Theory of Continued Fractions . Chelsea Publishing Company. pp. 374– 375. ^ Reinhardt & Walker (2010a) §22.20(ii) ^ Carlson (2010) §19.8 ^ Reinhardt & Walker (2010a) §22.12.12 ^ In general,
sinh
(
x
−
n
π
)
{\displaystyle \sinh(x-n\pi )}
sin
(
x
−
n
π
i
)
=
−
i
sinh
(
i
x
+
n
π
)
{\displaystyle \sin(x-n\pi i)=-i\sinh(ix+n\pi )}
^ Reinhardt & Walker (2010a) §22.11 ^ Reinhardt & Walker (2010a) §22.2.E7 ^ Berndt (1994) p. 247, 248, 253^ Reinhardt & Walker (2010a) §22.11.E1 ^ Whittaker & Watson (1927) ^ Borwein & Borwein (1987) ^ a b Eymard & Lafon (2004) p. 227.^ Cartan, H. (1961). Théorie élémentaire des fonctions analytiques d'une ou plusieurs variables complexes (in French). Hermann. pp. 160– 164. ^ More precisely, suppose
{
a
n
}
{\displaystyle \{a_{n}\}}
S
{\displaystyle S}
∑
|
a
n
(
z
)
|
{\textstyle \sum \left|a_{n}(z)\right|}
S
{\displaystyle S}
{
n
1
,
n
2
,
n
3
,
…
}
{\displaystyle \{n_{1},n_{2},n_{3},\ldots \}}
permutation of
{
1
,
2
,
3
,
…
}
{\displaystyle \{1,2,3,\ldots \}}
∏
n
=
1
∞
(
1
+
a
n
(
z
)
)
=
∏
k
=
1
∞
(
1
+
a
n
k
(
z
)
)
{\textstyle \prod _{n=1}^{\infty }(1+a_{n}(z))=\prod _{k=1}^{\infty }(1+a_{n_{k}}(z))}
z
∈
S
{\displaystyle z\in S}
bijection between the natural numbers and
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
^ Bottazzini & Gray (2013) p. 58^ More precisely, if for each
k
{\displaystyle k}
lim
n
→
∞
a
k
(
n
)
{\textstyle \lim _{n\to \infty }a_{k}(n)}
∑
k
=
1
∞
M
k
{\textstyle \sum _{k=1}^{\infty }M_{k}}
|
a
k
(
n
)
|
≤
M
k
{\displaystyle \left|a_{k}(n)\right|\leq M_{k}}
n
∈
N
{\displaystyle n\in \mathbb {N} }
1
≤
k
≤
n
{\displaystyle 1\leq k\leq n}
lim
n
→
∞
∑
k
=
1
n
a
k
(
n
)
=
∑
k
=
1
∞
lim
n
→
∞
a
k
(
n
)
.
{\displaystyle \lim _{n\to \infty }\sum _{k=1}^{n}a_{k}(n)=\sum _{k=1}^{\infty }\lim _{n\to \infty }a_{k}(n).}
^ Alternatively, it can be inferred that these expansions exist just from the analyticity of
M
{\displaystyle M}
N
{\displaystyle N}
∑
α
1
α
4
=
−
the coefficient of
z
5
{\textstyle \sum _{\alpha }{\frac {1}{\alpha ^{4}}}=-\,{\text{the coefficient of}}\,z^{5}}
M
{\displaystyle M}
^ Gauss, C. F. (1866). Werke (Band III)
φ
17
{\displaystyle \varphi ^{17}}
107
7
410
154
752
000
{\displaystyle {\tfrac {107}{7\,410\,154\,752\,000}}}
107
207
484
333
056
000
{\displaystyle {\tfrac {107}{207\,484\,333\,056\,000}}}
^ If
M
(
z
)
=
∑
n
=
0
∞
a
n
z
n
+
1
{\textstyle M(z)=\sum _{n=0}^{\infty }a_{n}z^{n+1}}
a
n
{\displaystyle a_{n}}
a
n
+
1
=
−
1
n
+
1
∑
k
=
0
n
2
n
−
k
+
1
a
k
H
n
−
k
+
1
(
n
−
k
+
1
)
!
{\textstyle a_{n+1}=-{\frac {1}{n+1}}\sum _{k=0}^{n}2^{n-k+1}a_{k}{\frac {\mathrm {H} _{n-k+1}}{(n-k+1)!}}}
a
0
=
1
{\displaystyle a_{0}=1}
H
n
{\displaystyle \mathrm {H} _{n}}
Lemniscate elliptic functions § Hurwitz numbers .
^ The power series expansions of
M
{\displaystyle M}
N
{\displaystyle N}
β
{\displaystyle \beta }
β
{\displaystyle \beta }
L
{\displaystyle {\mathcal {L}}}
β
=
m
+
n
i
{\displaystyle \beta =m+ni}
m
,
n
∈
Z
{\displaystyle m,n\in \mathbb {Z} }
m
+
n
{\displaystyle m+n}
3
{\displaystyle 3}
M
(
3
z
)
=
d
9
M
(
z
)
9
+
d
5
M
(
z
)
5
N
(
z
)
4
+
d
1
M
(
z
)
N
(
z
)
8
{\displaystyle M(3z)=d_{9}M(z)^{9}+d_{5}M(z)^{5}N(z)^{4}+d_{1}M(z)N(z)^{8}}
d
1
,
d
5
,
d
9
{\displaystyle d_{1},d_{5},d_{9}}
3
z
−
2
(
3
z
)
5
5
!
−
36
(
3
z
)
9
9
!
+
O
(
z
13
)
=
d
9
x
9
+
d
5
x
5
y
4
+
d
1
x
y
8
,
{\displaystyle 3z-2{\frac {(3z)^{5}}{5!}}-36{\frac {(3z)^{9}}{9!}}+\operatorname {O} (z^{13})=d_{9}x^{9}+d_{5}x^{5}y^{4}+d_{1}xy^{8},}
x
=
z
−
2
z
5
5
!
−
36
z
9
9
!
+
O
(
z
13
)
,
y
=
1
+
2
z
4
4
!
−
4
z
8
8
!
+
O
(
z
12
)
,
{\displaystyle x=z-2{\frac {z^{5}}{5!}}-36{\frac {z^{9}}{9!}}+\operatorname {O} (z^{13}),\quad y=1+2{\frac {z^{4}}{4!}}-4{\frac {z^{8}}{8!}}+\operatorname {O} (z^{12}),}
{
d
1
,
d
5
,
d
9
}
=
{
3
,
−
6
,
−
1
}
.
{\displaystyle \{d_{1},d_{5},d_{9}\}=\{3,-6,-1\}.}
3
{\displaystyle 3}
−
X
9
−
6
X
5
+
3
X
{\displaystyle -X^{9}-6X^{5}+3X}
sl
(
2
ϖ
/
3
)
{\displaystyle \operatorname {sl} (2\varpi /3)}
X
n
=
1
{\displaystyle X^{n}=1}
e
2
π
i
/
n
{\displaystyle e^{2\pi i/n}}
n
{\displaystyle n}
β
{\displaystyle \beta }
β
{\displaystyle \beta }
^ By utilizing the power series expansion of the
N
{\displaystyle N}
sl
(
2
ϖ
/
β
)
{\displaystyle \operatorname {sl} (2\varpi /\beta )}
β
{\displaystyle \beta }
∑
n
=
0
(
β
β
¯
−
1
)
/
4
a
4
n
+
1
(
β
)
X
β
β
¯
−
4
n
{\displaystyle \sum _{n=0}^{(\beta {\overline {\beta }}-1)/4}a_{4n+1}(\beta )X^{\beta {\overline {\beta }}-4n}}
a
1
(
β
)
=
1
,
a
5
(
β
)
=
β
4
−
β
β
¯
12
,
a
9
(
β
)
=
−
β
8
−
70
β
5
β
¯
+
336
β
4
+
35
β
2
β
¯
2
−
300
β
β
¯
10080
{\displaystyle {\begin{aligned}a_{1}(\beta )&=1,\\a_{5}(\beta )&={\frac {\beta ^{4}-\beta {\overline {\beta }}}{12}},\\a_{9}(\beta )&={\frac {-\beta ^{8}-70\beta ^{5}{\overline {\beta }}+336\beta ^{4}+35\beta ^{2}{\overline {\beta }}^{2}-300\beta {\overline {\beta }}}{10080}}\end{aligned}}}
^ Zhuravskiy, A. M. (1941). Spravochnik po ellipticheskim funktsiyam (in Russian). Izd. Akad. Nauk. U.S.S.R. ^ For example, by the quasi-addition formulas, the duplication formulas and the Pythagorean-like identities, we have
M
(
3
z
)
=
−
M
(
z
)
9
−
6
M
(
z
)
5
N
(
z
)
4
+
3
M
(
z
)
N
(
z
)
8
,
{\displaystyle M(3z)=-M(z)^{9}-6M(z)^{5}N(z)^{4}+3M(z)N(z)^{8},}
N
(
3
z
)
=
N
(
z
)
9
+
6
M
(
z
)
4
N
(
z
)
5
−
3
M
(
z
)
8
N
(
z
)
,
{\displaystyle N(3z)=N(z)^{9}+6M(z)^{4}N(z)^{5}-3M(z)^{8}N(z),}
sl
3
z
=
−
M
(
z
)
9
−
6
M
(
z
)
5
N
(
z
)
4
+
3
M
(
z
)
N
(
z
)
8
N
(
z
)
9
+
6
M
(
z
)
4
N
(
z
)
5
−
3
M
(
z
)
8
N
(
z
)
.
{\displaystyle \operatorname {sl} 3z={\frac {-M(z)^{9}-6M(z)^{5}N(z)^{4}+3M(z)N(z)^{8}}{N(z)^{9}+6M(z)^{4}N(z)^{5}-3M(z)^{8}N(z)}}.}
N
(
z
)
9
{\displaystyle N(z)^{9}}
sl
{\displaystyle \operatorname {sl} }
sl
3
z
=
−
sl
9
z
−
6
sl
5
z
+
3
sl
z
1
+
6
sl
4
z
−
3
sl
8
z
.
{\displaystyle \operatorname {sl} 3z={\frac {-\operatorname {sl} ^{9}z-6\operatorname {sl} ^{5}z+3\operatorname {sl} z}{1+6\operatorname {sl} ^{4}z-3\operatorname {sl} ^{8}z}}.}
^ Gauss (1866), p. 408
^ Robinson (2019a) ^ Eymard & Lafon (2004) p. 234^ Armitage, J. V.; Eberlein, W. F. (2006). Elliptic Functions . Cambridge University Press. p. 49. ISBN 978-0-521-78563-1 . ^ The identity
cl
z
=
cn
(
2
z
;
1
2
)
{\displaystyle \operatorname {cl} z={\operatorname {cn} }\left({\sqrt {2}}z;{\tfrac {1}{\sqrt {2}}}\right)}
Greenhill (1892) p. 33 .
^ Siegel (1969) ^ Sloane, N. J. A. (ed.). "Sequence A175576" . The On-Line Encyclopedia of Integer Sequences . OEIS Foundation.^ Berndt, Bruce C. (1989). Ramanujan's Notebooks Part II . Springer. ISBN 978-1-4612-4530-8 . ^ Levin (2006) ; Robinson (2019b) ^ Levin (2006) p. 515^ a b Cox (2012) p. 508, 509^ a b c d Arakawa, Tsuneo; Ibukiyama, Tomoyoshi; Kaneko, Masanobu (2014). Bernoulli Numbers and Zeta Functions . Springer. ISBN 978-4-431-54918-5 . ^ Equivalently,
H
n
=
−
lim
z
→
0
d
n
d
z
n
(
(
1
+
i
)
z
/
2
sl
(
(
1
+
i
)
z
/
2
)
+
z
2
E
(
z
2
;
i
)
)
{\displaystyle \mathrm {H} _{n}=-\lim _{z\to 0}{\frac {\mathrm {d} ^{n}}{\mathrm {d} z^{n}}}\left({\frac {(1+i)z/2}{\operatorname {sl} ((1+i)z/2)}}+{\frac {z}{2}}{\mathcal {E}}\left({\frac {z}{2}};i\right)\right)}
n
≥
4
{\displaystyle n\geq 4}
E
(
⋅
;
i
)
{\displaystyle {\mathcal {E}}(\cdot ;i)}
Jacobi epsilon function with modulus
i
{\displaystyle i}
^ The Bernoulli numbers can be determined by an analogous recurrence:
B
2
n
=
−
1
2
n
+
1
∑
k
=
1
n
−
1
(
2
n
2
k
)
B
2
k
B
2
(
n
−
k
)
{\displaystyle \mathrm {B} _{2n}=-{\frac {1}{2n+1}}\sum _{k=1}^{n-1}{\binom {2n}{2k}}\mathrm {B} _{2k}\mathrm {B} _{2(n-k)}}
n
≥
2
{\displaystyle n\geq 2}
B
2
=
1
/
6
{\displaystyle \mathrm {B} _{2}=1/6}
^ Katz, Nicholas M. (1975). "The congruences of Clausen — von Staudt and Kummer for Bernoulli-Hurwitz numbers". Mathematische Annalen . 216 (1): 1– 4. doi :10.1007/BF02547966 . ^ For more on the
ν
{\displaystyle \nu }
Lemniscate constant .
^ Hurwitz, Adolf (1963). Mathematische Werke: Band II (in German). Springer Basel AG. ^ Arakawa et al. (2014) define
H
4
n
{\displaystyle \mathrm {H} _{4n}}
1
/
sl
2
.
{\displaystyle 1/\operatorname {sl} ^{2}.}
^ Eisenstein, G. (1846). "Beiträge zur Theorie der elliptischen Functionen" . Journal für die reine und angewandte Mathematik (in German). 30 .
φ
=
sl
{\displaystyle \varphi =\operatorname {sl} }
ω
=
2
ϖ
{\displaystyle \omega =2\varpi }
^ Ogawa (2005) ^ Peirce (1879) . Guyou (1887) and Adams (1925) introduced transverse and oblique aspects of the same projection, respectively. Also see Lee (1976) . These authors write their projection formulas in terms of Jacobi elliptic functions, with a square lattice.^ Adams (1925) ^ Adams (1925) ; Lee (1976) .^ Rančić, Purser & Mesinger (1996) ; McGregor (2005) .
References
Abel, Niels Henrik (1827–1828) "Recherches sur les fonctions elliptiques" [Research on elliptic functions] (in French). Crelle's Journal Part 1 . 1827. 2 (2): 101–181. doi :10.1515/crll.1827.2.101 .Part 2 . 1828. 3 (3): 160–190. doi :10.1515/crll.1828.3.160 .Adams, Oscar S. (1925). Elliptic Functions Applied to Conformal World Maps (PDF) . U.S. Coast and Geodetic Survey. US Government Printing Office. Special Pub. No. 112.Ayoub, Raymond (1984). "The Lemniscate and Fagnano's Contributions to Elliptic Integrals". Archive for History of Exact Sciences . 29 (2): 131– 149. doi :10.1007/BF00348244 . Berndt, Bruce C. (1994). Ramanujan's Notebooks Part IV (First ed.). Springer. ISBN 978-1-4612-6932-8 . Borwein, Jonatham M. ; Borwein, Peter B. (1987). "2.7 The Landen Transformation". Pi and the AGM . Wiley-Interscience. p. 60.Bottazzini, Umberto ; Gray, Jeremy (2013). Hidden Harmony – Geometric Fantasies: The Rise of Complex Function Theory . Springer. doi :10.1007/978-1-4614-5725-1 . ISBN 978-1-4614-5724-4 .Carlson, Billie C. (2010). "19. Elliptic Integrals" . In Olver, Frank ; et al. (eds.). NIST Handbook of Mathematical Functions Cox, David Archibald (1984). "The Arithmetic-Geometric Mean of Gauss" . L'Enseignement Mathématique . 30 (2): 275– 330.Cox, David Archibald; Shurman, Jerry (2005). "Geometry and number theory on clovers" (PDF) . The American Mathematical Monthly . 112 (8): 682– 704. doi :10.1080/00029890.2005.11920241 . Cox, David Archibald (2012). "The Lemniscate". Galois Theory . Wiley. pp. 463– 514. doi :10.1002/9781118218457.ch15 . ISBN 978-1-118-07205-9 . Cox, David Archibald (2013). Primes of the Form x 2 + ny 2 Cox, David Archibald; Hyde, Trevor (2014). "The Galois theory of the lemniscate" (PDF) . Journal of Number Theory . 135 : 43– 59. arXiv :1208.2653 doi :10.1016/j.jnt.2013.08.006 . Enneper, Alfred (1890) [1st ed. 1876]. "Note III: Historische Notizen über geometrische Anwendungen elliptischer Integrale." [Historical notes on geometric applications of elliptic integrals]. Elliptische Functionen, Theorie und Geschichte (in German). Nebert. pp. 524– 547.Euler, Leonhard (1761). "Observationes de comparatione arcuum curvarum irrectificibilium" [Observations on the comparison of arcs of irrectifiable curves]. Novi Commentarii Academiae Scientiarum Imperialis Petropolitanae (in Latin). 6 : 58– 84.E 252 . (Figures )Euler, Leonhard (1786). "De miris proprietatibus curvae elasticae sub aequatione
y
=
∫
x
x
d
x
/
1
−
x
4
{\textstyle y=\int xx\mathop {\mathrm {d} x} {\big /}{\sqrt {1-x^{4}}}}
[On the amazing properties of elastic curves contained in equation
y
=
∫
x
x
d
x
/
1
−
x
4
{\textstyle y=\int xx\mathop {\mathrm {d} x} {\big /}{\sqrt {1-x^{4}}}}
Acta Academiae Scientiarum Imperialis Petropolitanae (in Latin). 1782 (2): 34– 61. 605 .Eymard, Pierre; Lafon, Jean-Pierre (2004). The Number Pi . Translated by Wilson, Stephen. American Mathematical Society. ISBN 0-8218-3246-8 . Fagnano, Giulio Carlo (1718–1723) "Metodo per misurare la lemniscata" [Method for measuring the lemniscate]. Giornale de' letterati d'Italia (in Italian)."Schediasma primo" [Part 1]. 1718. 29 : 258–269."Giunte al primo schediasma" [Addendum to part 1]. 1723. 34 : 197–207."Schediasma secondo" [Part 2]. 1718. 30 : 87–111.Fagnano (1850). "32–34. Metodo per misurare la lemniscata" . Opere Matematiche, vol. 2 . Allerighi e Segati. pp. 293– 313. Figures )Gauss, Carl Friedrich (1917). Werke (Band X, Abteilung I) Gómez-Molleda, M. A.; Lario, Joan-C. (2019). "Ruler and Compass Constructions of the Equilateral Triangle and Pentagon in the Lemniscate Curve". The Mathematical Intelligencer . 41 (4): 17– 21. doi :10.1007/s00283-019-09892-w . Greenhill, Alfred George (1892). The Applications of Elliptic Functions Guyou, Émile (1887). "Nouveau système de projection de la sphère: Généralisation de la projection de Mercator" [New system of projection of the sphere]. Annales Hydrographiques . Série 2 (in French). 9 : 16– 35. Houzel, Christian (1978). "Fonctions elliptiques et intégrales abéliennes" [Elliptic functions and Abelian integrals]. In Dieudonné, Jean (ed.). Abrégé d'histoire des mathématiques, 1700–1900. II (in French). Hermann. pp. 1– 113. Hyde, Trevor (2014). "A Wallis product on clovers" (PDF) . The American Mathematical Monthly . 121 (3): 237– 243. doi :10.4169/amer.math.monthly.121.03.237 . Kubota, Tomio (1964). "Some arithmetical applications of an elliptic function". Crelle's Journal . 214 /215 : 141– 145. doi :10.1515/crll.1964.214-215.141 .Langer, Joel C.; Singer, David A. (2010). "Reflections on the Lemniscate of Bernoulli: The Forty-Eight Faces of a Mathematical Gem" (PDF) . Milan Journal of Mathematics . 78 (2): 643– 682. doi :10.1007/s00032-010-0124-5 . Langer, Joel C.; Singer, David A. (2011). "The lemniscatic chessboard" . Forum Geometricorum . 11 : 183– 199. Lawden, Derek Frank (1989). Elliptic Functions and Applications . Applied Mathematical Sciences. Vol. 80. Springer-Verlag. doi :10.1007/978-1-4757-3980-0 . ISBN 978-1-4419-3090-3 .Lee, L. P. (1976). Conformal Projections Based on Elliptic Functions Cartographica Monographs . Vol. 16. Toronto: B. V. Gutsell, York University. ISBN 0-919870-16-3 .The Canadian Cartographer 13 Lemmermeyer, Franz (2000). Reciprocity Laws: From Euler to Eisenstein . Springer. ISBN 3-540-66957-4 . Levien, Raph (2008). The elastica: a mathematical history (PDF) (Technical report). University of California at Berkeley. UCB/EECS-2008-103.Levin, Aaron (2006). "A Geometric Interpretation of an Infinite Product for the Lemniscate Constant" (PDF) . The American Mathematical Monthly . 113 (6): 510– 520. doi :10.1080/00029890.2006.11920331 . JSTOR 27641976 . Lindqvist, Peter; Peetre, Jaak (2001). "Two Remarkable Identities, Called Twos, for Inverses to Some Abelian Integrals" (PDF) . The American Mathematical Monthly . 108 (5): 403– 410. doi :10.1080/00029890.2001.11919766 . Archived from the original (PDF) on 2022-05-28. Markushevich, Aleksei Ivanovich (1966). The Remarkable Sine Functions Markushevich, Aleksei Ivanovich (1992). Introduction to the Classical Theory of Abelian Functions . Translations of Mathematical Monographs. Vol. 96. American Mathematical Society. doi :10.1090/mmono/096 . ISBN 978-0-8218-4164-8 . McGregor, John L. (2005). C-CAM: Geometric Aspects and Dynamical Formulation CSIRO Atmospheric Research . 70. McKean, Henry ; Moll, Victor (1999). Elliptic Curves: Function Theory, Geometry, Arithmetic ISBN 9780521582285 .Milne-Thomson, Louis Melville (1964). "16. Jacobian Elliptic Functions and Theta Functions" . In Abramowitz, Milton ; Stegun, Irene Ann (eds.). Handbook of Mathematical Functions 567– 585.Neuman, Edward (2007). "On Gauss lemniscate functions and lemniscatic mean" (PDF) . Mathematica Pannonica . 18 (1): 77– 94.Nishimura, Ryo (2015). "New properties of the lemniscate function and its transformation" . Journal of Mathematical Analysis and Applications . 427 (1): 460– 468. doi :10.1016/j.jmaa.2015.02.066 Ogawa, Takuma (2005). "Similarities between the trigonometric function and the lemniscate function from arithmetic view point" . Tsukuba Journal of Mathematics . 29 (1). doi :10.21099/tkbjm/1496164894 Peirce, Charles Sanders (1879). "A Quincuncial Projection of the Sphere" . American Journal of Mathematics . 2 (4): 394– 397. doi :10.2307/2369491 JSTOR 2369491 Popescu-Pampu, Patrick (2016). What is the Genus? . Lecture Notes in Mathematics. Vol. 2162. Springer. doi :10.1007/978-3-319-42312-8 . ISBN 978-3-319-42311-1 . Prasolov, Viktor; Solovyev, Yuri (1997). "4. Abel's Theorem on Division of Lemniscate". Elliptic functions and elliptic integrals . Translations of Mathematical Monographs. Vol. 170. American Mathematical Society. doi :10.1090/mmono/170 . ISBN 978-0-8218-0587-9 . Rančić, Miodrag; Purser, R. James; Mesinger, Fedor (1996). "A global shallow-water model using an expanded spherical cube: Gnomonic versus conformal coordinates". Quarterly Journal of the Royal Meteorological Society . 122 (532): 959– 982. doi :10.1002/qj.49712253209 . Reinhardt, William P.; Walker, Peter L. (2010a). "22. Jacobian Elliptic Functions" . In Olver, Frank; et al. (eds.). NIST Handbook of Mathematical Functions Reinhardt, William P.; Walker, Peter L. (2010b). "23. Weierstrass Elliptic and Modular Functions" . In Olver, Frank; et al. (eds.). NIST Handbook of Mathematical Functions Robinson, Paul L. (2019a). The Lemniscatic Functions arXiv :1902.08614 Robinson, Paul L. (2019b). The Elliptic Functions in a First-Order System arXiv :1903.07147 Rosen, Michael (1981). "Abel's Theorem on the Lemniscate". The American Mathematical Monthly . 88 (6): 387– 395. doi :10.1080/00029890.1981.11995279 . JSTOR 2321821 .Roy, Ranjan (2017). Elliptic and Modular Functions from Gauss to Dedekind to Hecke . Cambridge University Press. p. 28. ISBN 978-1-107-15938-9 . Schappacher, Norbert (1997). "Some milestones of lemniscatomy" (PDF) . In Sertöz, S. (ed.). Algebraic Geometry (Proceedings of Bilkent Summer School, August 7–19, 1995, Ankara, Turkey). Marcel Dekker. pp. 257– 290.Schneider, Theodor (1937). "Arithmetische Untersuchungen elliptischer Integrale" [Arithmetic investigations of elliptic integrals]. Mathematische Annalen (in German). 113 (1): 1– 13. doi :10.1007/BF01571618 .Schwarz, Hermann Amandus (1869). "Ueber einige Abbildungsaufgaben" [About some mapping problems]. Crelle's Journal (in German). 70 : 105– 120. doi :10.1515/crll.1869.70.105 .Siegel, Carl Ludwig (1969). "1. Elliptic Functions". Topics in Complex Function Theory, Vol. I . Wiley-Interscience. pp. 1– 89. ISBN 0-471-60844-0 .Snape, Jamie (2004). "Bernoulli's Lemniscate" . Applications of Elliptic Functions in Classical and Algebraic Geometry (Thesis). University of Durham. pp. 50– 56. Southard, Thomas H. (1964). "18. Weierstrass Elliptic and Related Functions" . In Abramowitz, Milton ; Stegun, Irene Ann (eds.). Handbook of Mathematical Functions 627– 683. Sridharan, Ramaiyengar (2004) "Physics to Mathematics: from Lintearia to Lemniscate". Resonance . "Part I" . 9 (4): 21–29. doi :10.1007/BF02834853 . "Part II: Gauss and Landen's Work" . 9 (6): 11–20. doi :10.1007/BF02839214 .Todd, John (1975). "The lemniscate constants" . Communications of the ACM . 18 (1): 14– 19. doi :10.1145/360569.360580 Whittaker, Edmund Taylor ; Watson, George Neville (1920) [1st ed. 1902]. "22.8 The lemniscate functions" . A Course of Modern Analysis 524– 528.Whittaker, Edmund Taylor ; Watson, George Neville (1927) [4th ed. 1927]. "21 The theta functions". A Course of Modern Analysis 469– 470.
External links

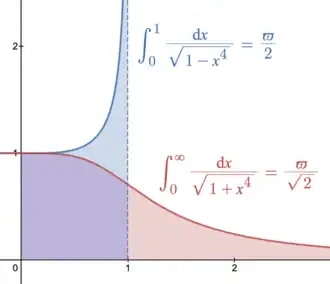
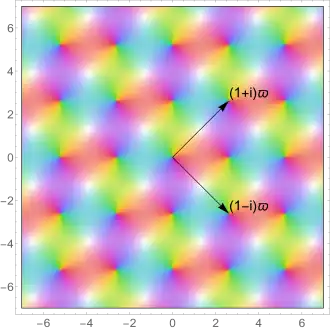
_%253D_a(1_-_x%C2%B2y%C2%B2)_for_various_values_of_a.png)