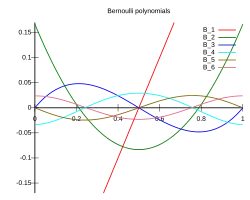
Bernoulli polynomials

In mathematics, the Bernoulli polynomials, named after Jacob Bernoulli, combine the Bernoulli numbers and binomial coefficients. They are used for series expansion of functions, and with the Euler–MacLaurin formula.

These polynomials occur in the study of many special functions and, in particular, the Riemann zeta function and the Hurwitz zeta function. They are an Appell sequence (i.e. a Sheffer sequence for the ordinary derivative operator). For the Bernoulli polynomials, the number of crossings of the x-axis in the unit interval does not go up with the degree. In the limit of large degree, they approach, when appropriately scaled, the sine and cosine functions.

A similar set of polynomials, based on a generating function, is the family of Euler polynomials.

The Bernoulli polynomials B_n can be defined by a generating function. They also admit a variety of derived representations.

The generating function for the Bernoulli polynomials is $${\displaystyle {\frac {te^{xt}}{e^{t}-1}}=\sum _{n=0}^{\infty }B_{n}(x){\frac {t^{n}}{n!}}.}$$ The generating function for the Euler polynomials is $${\displaystyle {\frac {2e^{xt}}{e^{t}+1}}=\sum _{n=0}^{\infty }E_{n}(x){\frac {t^{n}}{n!}}.}$$

$${\displaystyle B_{n}(x)=\sum _{k=0}^{n}{n \choose k}B_{n-k}x^{k},}$$ $${\displaystyle E_{m}(x)=\sum _{k=0}^{m}{m \choose k}{\frac {E_{k}}{2^{k}}}\left(x-{\tfrac {1}{2}}\right)^{m-k}.}$$ for ${\displaystyle n\geq 0}$, where ${\displaystyle B_{k}}$ are the Bernoulli numbers, and ${\displaystyle E_{k}}$ are the Euler numbers. It follows that ${\displaystyle B_{n}(0)=B_{n}}$ and ${\displaystyle E_{m}{\big (}{\tfrac {1}{2}}{\big )}={\tfrac {1}{2^{m}}}E_{m}}$.

The Bernoulli polynomials are also given by $${\displaystyle \ B_{n}(x)={\frac {D}{\ e^{D}-1\ }}\ x^{n}\ }$$ where ${\displaystyle \ D\equiv {\frac {\mathrm {d} }{\ \mathrm {d} x\ }}\ }$ is differentiation with respect to x and the fraction is expanded as a formal power series. It follows that $${\displaystyle \ \int _{a}^{x}\ B_{n}(u)\ \mathrm {d} \ u={\frac {\ B_{n+1}(x)-B_{n+1}(a)\ }{n+1}}~.}$$ cf. § Integrals below. By the same token, the Euler polynomials are given by $${\displaystyle \ E_{n}(x)={\frac {2}{\ e^{D}+1\ }}\ x^{n}~.}$$

The Bernoulli polynomials are also the unique polynomials determined by $${\displaystyle \int _{x}^{x+1}B_{n}(u)\,du=x^{n}.}$$

The integral transform $${\displaystyle (Tf)(x)=\int _{x}^{x+1}f(u)\,du}$$ on polynomials f, simply amounts to $${\displaystyle {\begin{aligned}(Tf)(x)={e^{D}-1 \over D}f(x)&{}=\sum _{n=0}^{\infty }{D^{n} \over (n+1)!}f(x)\\&{}=f(x)+{f'(x) \over 2}+{f''(x) \over 6}+{f'''(x) \over 24}+\cdots .\end{aligned}}}$$ This can be used to produce the inversion formulae below.

In,^[1][2] it is deduced and proved that the Bernoulli polynomials can be obtained by the following integral recurrence $${\displaystyle B_{m}(x)=m\int _{0}^{x}B_{m-1}(t)\,dt-m\int _{0}^{1}\int _{0}^{t}B_{m-1}(s)\,dsdt.}$$

An explicit formula for the Bernoulli polynomials is given by $${\displaystyle B_{n}(x)=\sum _{k=0}^{n}{\biggl [}{\frac {1}{k+1}}\sum _{\ell =0}^{k}(-1)^{\ell }{k \choose \ell }(x+\ell )^{n}{\biggr ]}.}$$

That is similar to the series expression for the Hurwitz zeta function in the complex plane. Indeed, there is the relationship $${\displaystyle B_{n}(x)=-n\zeta (1-n,\,x)}$$ where ${\displaystyle \zeta (s,\,q)}$ is the Hurwitz zeta function. The latter generalizes the Bernoulli polynomials, allowing for non-integer values of n.

The inner sum may be understood to be the nth forward difference of ${\displaystyle x^{m},}$ that is, $${\displaystyle \Delta ^{n}x^{m}=\sum _{k=0}^{n}(-1)^{n-k}{n \choose k}(x+k)^{m}}$$ where ${\displaystyle \Delta }$ is the forward difference operator. Thus, one may write $${\displaystyle B_{n}(x)=\sum _{k=0}^{n}{\frac {(-1)^{k}}{k+1}}\Delta ^{k}x^{n}.}$$

This formula may be derived from an identity appearing above as follows. Since the forward difference operator Δ equals $${\displaystyle \Delta =e^{D}-1}$$ where D is differentiation with respect to x, we have, from the Mercator series, $${\displaystyle {\frac {D}{e^{D}-1}}={\frac {\log(\Delta +1)}{\Delta }}=\sum _{n=0}^{\infty }{\frac {(-\Delta )^{n}}{n+1}}.}$$

As long as this operates on an mth-degree polynomial such as ${\displaystyle x^{m},}$ one may let n go from 0 only up to m.

An integral representation for the Bernoulli polynomials is given by the Nörlund–Rice integral, which follows from the expression as a finite difference.

An explicit formula for the Euler polynomials is given by $${\displaystyle E_{n}(x)=\sum _{k=0}^{n}\left[{\frac {1}{2^{k}}}\sum _{\ell =0}^{n}(-1)^{\ell }{k \choose \ell }(x+\ell )^{n}\right].}$$

The above follows analogously, using the fact that $${\displaystyle {\frac {2}{e^{D}+1}}={\frac {1}{1+{\tfrac {1}{2}}\Delta }}=\sum _{n=0}^{\infty }{\bigl (}{-{\tfrac {1}{2}}}\Delta {\bigr )}^{n}.}$$

Using either the above integral representation of ${\displaystyle x^{n}}$ or the identity ${\displaystyle B_{n}(x+1)-B_{n}(x)=nx^{n-1}}$, we have $${\displaystyle \sum _{k=0}^{x}k^{p}=\int _{0}^{x+1}B_{p}(t)\,dt={\frac {B_{p+1}(x+1)-B_{p+1}}{p+1}}}$$ (assuming 0⁰ = 1).

The first few Bernoulli polynomials are: $${\displaystyle {\begin{aligned}B_{0}(x)&=1,&B_{4}(x)&=x^{4}-2x^{3}+x^{2}-{\tfrac {1}{30}},\\[4mu]B_{1}(x)&=x-{\tfrac {1}{2}},&B_{5}(x)&=x^{5}-{\tfrac {5}{2}}x^{4}+{\tfrac {5}{3}}x^{3}-{\tfrac {1}{6}}x,\\[4mu]B_{2}(x)&=x^{2}-x+{\tfrac {1}{6}},&B_{6}(x)&=x^{6}-3x^{5}+{\tfrac {5}{2}}x^{4}-{\tfrac {1}{2}}x^{2}+{\tfrac {1}{42}},\\[-2mu]B_{3}(x)&=x^{3}-{\tfrac {3}{2}}x^{2}+{\tfrac {1}{2}}x{\vphantom {\Big |}},\qquad &&\ \,\,\vdots \end{aligned}}}$$

The first few Euler polynomials are: $${\displaystyle {\begin{aligned}E_{0}(x)&=1,&E_{4}(x)&=x^{4}-2x^{3}+x,\\[4mu]E_{1}(x)&=x-{\tfrac {1}{2}},&E_{5}(x)&=x^{5}-{\tfrac {5}{2}}x^{4}+{\tfrac {5}{2}}x^{2}-{\tfrac {1}{2}},\\[4mu]E_{2}(x)&=x^{2}-x,&E_{6}(x)&=x^{6}-3x^{5}+5x^{3}-3x,\\[-1mu]E_{3}(x)&=x^{3}-{\tfrac {3}{2}}x^{2}+{\tfrac {1}{4}},\qquad \ \ &&\ \,\,\vdots \end{aligned}}}$$

At higher n the amount of variation in ${\displaystyle B_{n}(x)}$ between ${\displaystyle x=0}$ and ${\displaystyle x=1}$ gets large. For instance, ${\displaystyle B_{16}(0)=B_{16}(1)={}}$${\displaystyle -{\tfrac {3617}{510}}\approx -7.09,}$ but ${\displaystyle B_{16}{\bigl (}{\tfrac {1}{2}}{\bigr )}={}}$${\displaystyle {\tfrac {118518239}{3342336}}\approx 7.09.}$ Lehmer (1940)^[3] showed that the maximum value (M_n) of ${\displaystyle B_{n}(x)}$ between 0 and 1 obeys $${\displaystyle M_{n}<{\frac {2n!}{(2\pi )^{n}}}}$$ unless n is 2 modulo 4, in which case $${\displaystyle M_{n}={\frac {2\zeta (n)\,n!}{(2\pi )^{n}}}}$$ (where ${\displaystyle \zeta (x)}$ is the Riemann zeta function), while the minimum (m_n) obeys $${\displaystyle m_{n}>{\frac {-2n!}{(2\pi )^{n}}}}$$ unless n = 0 modulo 4 , in which case $${\displaystyle m_{n}={\frac {-2\zeta (n)\,n!}{(2\pi )^{n}}}.}$$

These limits are quite close to the actual maximum and minimum, and Lehmer gives more accurate limits as well.

The Bernoulli and Euler polynomials obey many relations from umbral calculus: $${\displaystyle {\begin{aligned}\Delta B_{n}(x)&=B_{n}(x+1)-B_{n}(x)=nx^{n-1},\\[3mu]\Delta E_{n}(x)&=E_{n}(x+1)-E_{n}(x)=2(x^{n}-E_{n}(x)).\end{aligned}}}$$ (Δ is the forward difference operator). Also, $${\displaystyle E_{n}(x+1)+E_{n}(x)=2x^{n}.}$$ These polynomial sequences are Appell sequences: $${\displaystyle {\begin{aligned}B_{n}'(x)&=nB_{n-1}(x),\\[3mu]E_{n}'(x)&=nE_{n-1}(x).\end{aligned}}}$$

$${\displaystyle {\begin{aligned}B_{n}(x+y)&=\sum _{k=0}^{n}{n \choose k}B_{k}(x)y^{n-k}\\[3mu]E_{n}(x+y)&=\sum _{k=0}^{n}{n \choose k}E_{k}(x)y^{n-k}\end{aligned}}}$$ These identities are also equivalent to saying that these polynomial sequences are Appell sequences. (Hermite polynomials are another example.)

$${\displaystyle {\begin{aligned}B_{n}(1-x)&=\left(-1\right)^{n}B_{n}(x),&&n\geq 0,{\text{ and in particular for }}n\neq 1,~B_{n}(0)=B_{n}(1)\\[3mu]E_{n}(1-x)&=\left(-1\right)^{n}E_{n}(x)\\[1ex]\left(-1\right)^{n}B_{n}(-x)&=B_{n}(x)+nx^{n-1}\\[3mu]\left(-1\right)^{n}E_{n}(-x)&=-E_{n}(x)+2x^{n}\\[1ex]B_{n}{\bigl (}{\tfrac {1}{2}}{\bigr )}&=\left({\frac {1}{2^{n-1}}}-1\right)B_{n},&&n\geq 0{\text{ from the multiplication theorems below.}}\end{aligned}}}$$ Zhi-Wei Sun and Hao Pan ^[4] established the following surprising symmetry relation: If r + s + t = n and x + y + z = 1, then $${\displaystyle r[s,t;x,y]_{n}+s[t,r;y,z]_{n}+t[r,s;z,x]_{n}=0,}$$ where $${\displaystyle [s,t;x,y]_{n}=\sum _{k=0}^{n}(-1)^{k}{s \choose k}{t \choose {n-k}}B_{n-k}(x)B_{k}(y).}$$

The Fourier series of the Bernoulli polynomials is also a Dirichlet series, given by the expansion $${\displaystyle B_{n}(x)=-{\frac {n!}{(2\pi i)^{n}}}\sum _{k\not =0}{\frac {e^{2\pi ikx}}{k^{n}}}=-2n!\sum _{k=1}^{\infty }{\frac {\cos \left(2k\pi x-{\frac {n\pi }{2}}\right)}{(2k\pi )^{n}}}.}$$ Note the simple large n limit to suitably scaled trigonometric functions.

This is a special case of the analogous form for the Hurwitz zeta function $${\displaystyle B_{n}(x)=-\Gamma (n+1)\sum _{k=1}^{\infty }{\frac {\exp(2\pi ikx)+e^{i\pi n}\exp(2\pi ik(1-x))}{(2\pi ik)^{n}}}.}$$

This expansion is valid only for 0 ≤ x ≤ 1 when n ≥ 2 and is valid for 0 < x < 1 when n = 1.

The Fourier series of the Euler polynomials may also be calculated. Defining the functions $${\displaystyle {\begin{aligned}C_{\nu }(x)&=\sum _{k=0}^{\infty }{\frac {\cos((2k+1)\pi x)}{(2k+1)^{\nu }}}\\[3mu]S_{\nu }(x)&=\sum _{k=0}^{\infty }{\frac {\sin((2k+1)\pi x)}{(2k+1)^{\nu }}}\end{aligned}}}$$ for ${\displaystyle \nu >1}$, the Euler polynomial has the Fourier series $${\displaystyle {\begin{aligned}C_{2n}(x)&={\frac {\left(-1\right)^{n}}{4(2n-1)!}}\pi ^{2n}E_{2n-1}(x)\\[1ex]S_{2n+1}(x)&={\frac {\left(-1\right)^{n}}{4(2n)!}}\pi ^{2n+1}E_{2n}(x).\end{aligned}}}$$ Note that the ${\displaystyle C_{\nu }}$ and ${\displaystyle S_{\nu }}$ are odd and even, respectively:$${\displaystyle {\begin{aligned}C_{\nu }(x)&=-C_{\nu }(1-x)\\S_{\nu }(x)&=S_{\nu }(1-x).\end{aligned}}}$$

They are related to the Legendre chi function ${\displaystyle \chi _{\nu }}$ as $${\displaystyle {\begin{aligned}C_{\nu }(x)&=\operatorname {Re} \chi _{\nu }(e^{ix})\\S_{\nu }(x)&=\operatorname {Im} \chi _{\nu }(e^{ix}).\end{aligned}}}$$

The Bernoulli and Euler polynomials may be inverted to express the monomial in terms of the polynomials.

Specifically, evidently from the above section on integral operators, it follows that $${\displaystyle x^{n}={\frac {1}{n+1}}\sum _{k=0}^{n}{n+1 \choose k}B_{k}(x)}$$ and $${\displaystyle x^{n}=E_{n}(x)+{\frac {1}{2}}\sum _{k=0}^{n-1}{n \choose k}E_{k}(x).}$$

The Bernoulli polynomials may be expanded in terms of the falling factorial ${\displaystyle (x)_{k}}$ as $${\displaystyle B_{n+1}(x)=B_{n+1}+\sum _{k=0}^{n}{\frac {n+1}{k+1}}\left\{{\begin{matrix}n\\k\end{matrix}}\right\}(x)_{k+1}}$$ where ${\displaystyle B_{n}=B_{n}(0)}$ and $${\displaystyle \left\{{\begin{matrix}n\\k\end{matrix}}\right\}=S(n,k)}$$ denotes the Stirling number of the second kind. The above may be inverted to express the falling factorial in terms of the Bernoulli polynomials: $${\displaystyle (x)_{n+1}=\sum _{k=0}^{n}{\frac {n+1}{k+1}}\left[{\begin{matrix}n\\k\end{matrix}}\right]\left(B_{k+1}(x)-B_{k+1}\right)}$$ where $${\displaystyle \left[{\begin{matrix}n\\k\end{matrix}}\right]=s(n,k)}$$ denotes the Stirling number of the first kind.

The multiplication theorems were given by Joseph Ludwig Raabe in 1851:

For a natural number m≥1, $${\displaystyle B_{n}(mx)=m^{n-1}\sum _{k=0}^{m-1}B_{n}{\left(x+{\frac {k}{m}}\right)}}$$ $${\displaystyle {\begin{aligned}E_{n}(mx)&=m^{n}\sum _{k=0}^{m-1}\left(-1\right)^{k}E_{n}{\left(x+{\frac {k}{m}}\right)}&{\text{ for odd }}m\\[1ex]E_{n}(mx)&={\frac {-2}{n+1}}m^{n}\sum _{k=0}^{m-1}\left(-1\right)^{k}B_{n+1}{\left(x+{\frac {k}{m}}\right)}&{\text{ for even }}m\end{aligned}}}$$

Two definite integrals relating the Bernoulli and Euler polynomials to the Bernoulli and Euler numbers are:^[5]

• ${\displaystyle \int _{0}^{1}B_{n}(t)B_{m}(t)\,dt=(-1)^{n-1}{\frac {m!\,n!}{(m+n)!}}B_{n+m}\quad {\text{for }}m,n\geq 1}$
• ${\displaystyle \int _{0}^{1}E_{n}(t)E_{m}(t)\,dt=(-1)^{n}4(2^{m+n+2}-1){\frac {m!\,n!}{(m+n+2)!}}B_{n+m+2}}$

Another integral formula states^[6]

• ${\displaystyle \int _{0}^{1}E_{n}\left(x+y\right)\log(\tan {\frac {\pi }{2}}x)\,dx=n!\sum _{k=1}^{\left\lfloor {\frac {n+1}{2}}\right\rfloor }{\frac {(-1)^{k-1}}{\pi ^{2k}}}\left(2-2^{-2k}\right)\zeta (2k+1){\frac {y^{n+1-2k}}{(n+1-2k)!}}}$

with the special case for ${\displaystyle y=0}$

• ${\displaystyle \int _{0}^{1}E_{2n-1}\left(x\right)\log(\tan {\frac {\pi }{2}}x)\,dx={\frac {(-1)^{n-1}(2n-1)!}{\pi ^{2n}}}\left(2-2^{-2n}\right)\zeta (2n+1)}$
• ${\displaystyle \int _{0}^{1}B_{2n-1}\left(x\right)\log(\tan {\frac {\pi }{2}}x)\,dx={\frac {(-1)^{n-1}}{\pi ^{2n}}}{\frac {2^{2n-2}}{(2n-1)!}}\sum _{k=1}^{n}(2^{2k+1}-1)\zeta (2k+1)\zeta (2n-2k)}$
• ${\displaystyle \int _{0}^{1}E_{2n}\left(x\right)\log(\tan {\frac {\pi }{2}}x)\,dx=\int _{0}^{1}B_{2n}\left(x\right)\log(\tan {\frac {\pi }{2}}x)\,dx=0}$
• ${\displaystyle \int _{0}^{1}{{{B}_{2n-1}}\left(x\right)\cot \left(\pi x\right)dx}={\frac {2\left(2n-1\right)!}{{{\left(-1\right)}^{n-1}}{{\left(2\pi \right)}^{2n-1}}}}\zeta \left(2n-1\right)}$

A periodic Bernoulli polynomial P_n(x) is a Bernoulli polynomial evaluated at the fractional part of the argument x. These functions are used to provide the remainder term in the Euler–Maclaurin formula relating sums to integrals. The first polynomial is a sawtooth function.

Strictly these functions are not polynomials at all and more properly should be termed the periodic Bernoulli functions, and P₀(x) is not even a function, being the derivative of a sawtooth and so a Dirac comb.

The following properties are of interest, valid for all ${\displaystyle x}$:

• ${\displaystyle P_{k}(x)}$ is continuous for all ${\displaystyle k>1}$
• ${\displaystyle P_{k}'(x)}$ exists and is continuous for ${\displaystyle k>2}$
• ${\displaystyle P'_{k}(x)=kP_{k-1}(x)}$ for ${\displaystyle k>2}$

• Bernoulli numbers
• Bernoulli polynomials of the second kind
• Stirling polynomial
• Polynomials calculating sums of powers of arithmetic progressions

• A list of integral identities involving Bernoulli polynomials from NIST