5-orthoplex honeycomb
| 5-orthoplex honeycomb | |
|---|---|
| (No image) | |
| Type | Hyperbolic regular honeycomb |
| Schläfli symbol | {3,3,3,4,3} |
| Coxeter diagram | |
| 5-faces |  {3,3,3,4} {3,3,3,4}
|
| 4-faces | |
| Cells |  {3,3} {3,3}
|
| Faces | 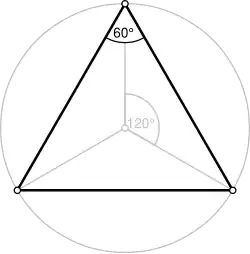 {3} {3}
|
| Cell figure |  {3} {3}
|
| Face figure |  {4,3} {4,3}
|
| Edge figure | |
| Vertex figure |  {3,3,4,3} {3,3,4,3}
|
| Dual | 24-cell honeycomb honeycomb |
| Coxeter group | U5, [3,3,3,4,3] |
| Properties | Regular |
In the geometry of hyperbolic 5-space, the 5-orthoplex honeycomb is one of five paracompact regular space-filling tessellations (or honeycombs). It is paracompact because it has infinite vertex figures, with all vertices as ideal points at infinity. With Schläfli symbol {3,3,3,4,3}, it has three 5-orthoplexes around each cell. It is dual to the 24-cell honeycomb honeycomb.
Related honeycombs
Its vertex figure is the 16-cell honeycomb, {3,3,4,3}.