17 equal temperament

Figure 1: 17-ET on the regular diatonic tuning continuum at P5=705.88 cents.[1]

In music, 17 equal temperament is the tempered scale derived by dividing the octave into 17 equal steps (equal frequency ratios). Each step represents a frequency ratio of 17√2, or 70.6 cents.

17-ET is the tuning of the regular diatonic tuning in which the tempered perfect fifth is equal to 705.88 cents, as shown in Figure 1 (look for the label "17-TET").

History and use

Alexander J. Ellis refers to a tuning of seventeen tones based on perfect fourths and fifths as the Arabic scale.[2] In the thirteenth century, Middle-Eastern musician Safi al-Din Urmawi developed a theoretical system of seventeen tones to describe Arabic and Persian music, although the tones were not equally spaced. This 17-tone system remained the primary theoretical system until the development of the quarter tone scale.

Notation

Notation of Easley Blackwood[3] for 17 equal temperament: intervals are notated similarly to those they approximate and enharmonic equivalents are distinct from those of 12 equal temperament (e.g., A♯/C♭).

Easley Blackwood Jr. created a notation system where sharps and flats raised/lowered 2 steps, identical to ups and downs notation for 17-EDO. ((10*7) mod 17 = 2.) This yields the chromatic scale:

C, D♭, C♯, D, E♭, D♯, E, F, G♭, F♯, G, A♭, G♯, A, B♭, A♯, B, C

Quarter tone sharps and flats can also be used, yielding the following chromatic scale:

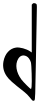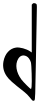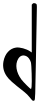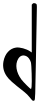C, Chalf sharp/D♭, C♯/Dhalf flat, D, Dhalf sharp/E♭, D♯/Ehalf flat, E, F, Fhalf sharp/G♭, F♯/Ghalf flat, G, Ghalf sharp/A♭, G♯/Ahalf flat, A, Ahalf sharp/B♭, A♯/Bhalf flat, B, C

Interval size

Below are some intervals in 17 EDO compared to just.

Major chord on C in 17 EDO : All notes are within 37 cents of just intonation (rather than 14 cents for 12 EDO).
17 EDO
just
12 EDO
I–IV–V–I chord progression in 17 EDO.[4] Whereas in 12 EDO, B♮ is 11 steps, in 17 EDO, B♮ is 16 steps.
interval name size
(steps) 		size
(cents) 		MIDI
audio 		just
ratio 		just
(cents) 		MIDI
audio 		error
octave 17 1200 2:1 1200 0
minor seventh 14 988.23 16:9 996.09 −7.77
harmonic seventh 14 988.23 7:4 968.83 +19.41
perfect fifth 10 705.88 3:2 701.96 +3.93
septimal tritone 8 564.71 7:5 582.51 −17.81
tridecimal narrow tritone 8 564.71 18:13 563.38 +1.32
undecimal super-fourth 8 564.71 11:8 551.32 +13.39
perfect fourth 7 494.12 4:3 498.04 −3.93
septimal major third 6 423.53 9:7 435.08 −11.55
undecimal major third 6 423.53 14:11 417.51 +6.02
major third 5 352.94 5:4 386.31 −33.37
tridecimal neutral third 5 352.94 16:13 359.47 −6.53
undecimal neutral third 5 352.94 11:9 347.41 +5.53
minor third 4 282.35 6:5 315.64 −33.29
tridecimal minor third 4 282.35 13:11 289.21 −6.86
septimal minor third 4 282.35 7:6 266.87 +15.48
septimal whole tone 3 211.76 8:7 231.17 −19.41
greater whole tone 3 211.76 9:8 203.91 +7.85
lesser whole tone 3 211.76 10:9 182.40 +29.36
neutral second, lesser undecimal 2 141.18 12:11 150.64 −9.46
greater tridecimal ⁠ 2 / 3 ⁠-tone 2 141.18 13:12 138.57 +2.60
lesser tridecimal ⁠ 2 / 3 ⁠-tone 2 141.18 14:13 128.30 +12.88
septimal diatonic semitone 2 141.18 15:14 119.44 +21.73
diatonic semitone 2 141.18 16:15 111.73 +29.45
septimal chromatic semitone 1 70.59 21:20 84.47 −13.88
chromatic semitone 1 70.59 25:24 70.67 −0.08

Relation to 34 EDO

17 EDO is a subset of 34 EDO, equivalent to every other step in the 34 EDO scale.

References

  1. ^ Milne, Sethares & Plamondon 2007, pp. 15–32.
  2. ^ Ellis, Alexander J. (1863). "On the Temperament of Musical Instruments with Fixed Tones", Proceedings of the Royal Society of London, vol. 13. (1863–1864), pp. 404–422.
  3. ^ Blackwood, Easley (Summer 1991). "Modes and Chord Progressions in Equal Tunings". Perspectives of New Music. 29 (2): 166–200 (175). doi:10.2307/833437. JSTOR 833437.
  4. ^ Milne, Sethares & Plamondon (2007), p. 29.

Sources

This article is issued from Wikipedia. The text is available under Creative Commons Attribution-Share Alike 4.0 unless otherwise noted. Additional terms may apply for the media files.